Презентация на тему: Повторение темы _Основы логики

Основы логики Автор: Подоплелова Надежда Ивановна Место работы: МБОУ Шарангская СОШ Должность: учитель информатики Презентация к урокам информатики в 10 классе

Как человек мыслит? Основоположник формальной логики – Аристотель, который впервые отделил логические формы мышления от его содержания.

Логика – наука о формах и способах мышления, учение о способах рассуждений и доказательств. Мышление осуществляется через понятия, высказывания и умозаключения. Понятие – форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличить их от других. Высказывание – это формулировка понимания окружающего мира (повествовательное суждение, в котором что-либо утверждается или отрицается, может быть истинным или ложным). Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Алгебра логики – отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказываний. Логическая переменная – простое высказывание, содержащее одну мысль. Обозначается латинскими буквами. Значением логической переменной могут быть только константы «истина» (1) или «ложь» (0). Логическая функция – составное высказывание F(А,В,С…), т.е. простые высказывания, соединённые с помощью логических операций. Логические операции – логические действия (конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность)

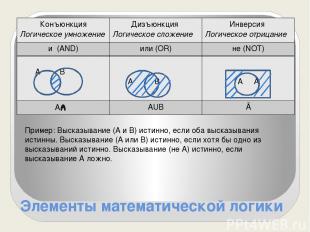
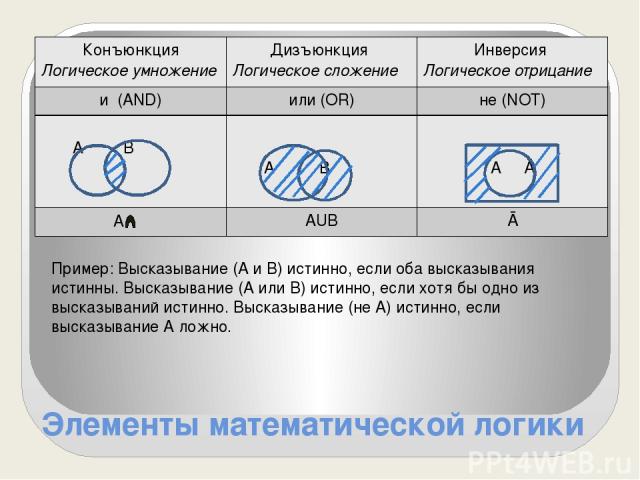
Элементы математической логики Пример: Высказывание (А и В) истинно, если оба высказывания истинны. Высказывание (А или В) истинно, если хотя бы одно из высказываний истинно. Высказывание (не А) истинно, если высказывание А ложно. Конъюнкция Логическое умножение Дизъюнкция Логическое сложение Инверсия Логическое отрицание и(AND) или(OR) не(NOT) А В А В АĀ AΒ AUB Ā

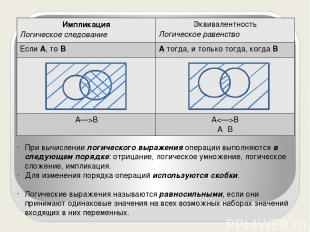
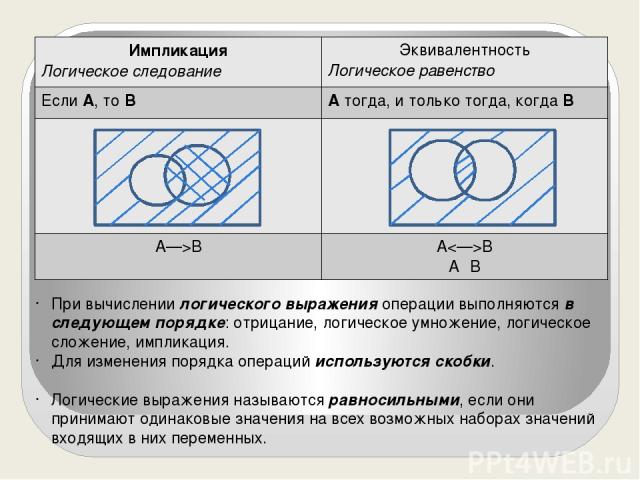
При вычислении логического выражения операции выполняются в следующем порядке: отрицание, логическое умножение, логическое сложение, импликация. Для изменения порядка операций используются скобки. Логические выражения называются равносильными, если они принимают одинаковые значения на всех возможных наборах значений входящих в них переменных. Импликация Логическое следование Эквивалентность Логическое равенство ЕслиА,тоВ Атогда, и толькотогда, когдаВ A—>B AB AΞB

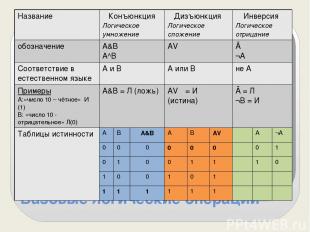
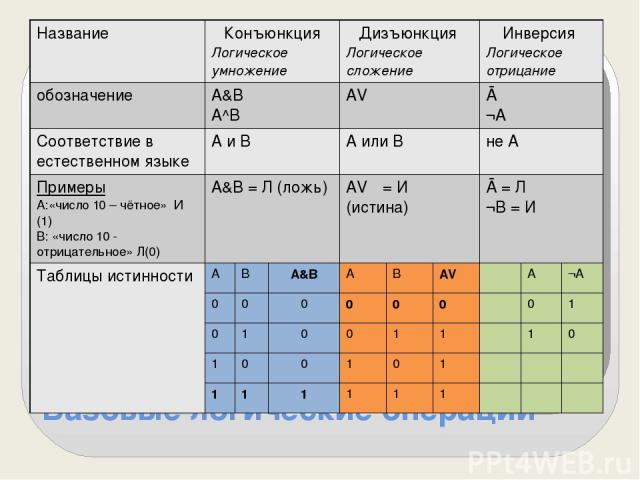
Базовые логические операции Название Конъюнкция Логическое умножение Дизъюнкция Логическое сложение Инверсия Логическое отрицание обозначение А&B А^В AVΒ Ā ¬A Соответствие в естественномязыке А и В А или В не А Примеры А:«число 10 – чётное» И (1) В: «число 10 - отрицательное» Л(0) А&B= Л (ложь) AVΒ= И (истина) Ā= Л ¬В= И Таблицы истинности А В А&B А В AVΒ А ¬A 0 0 0 0 0 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1

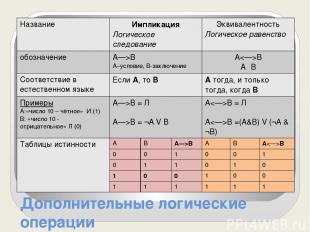
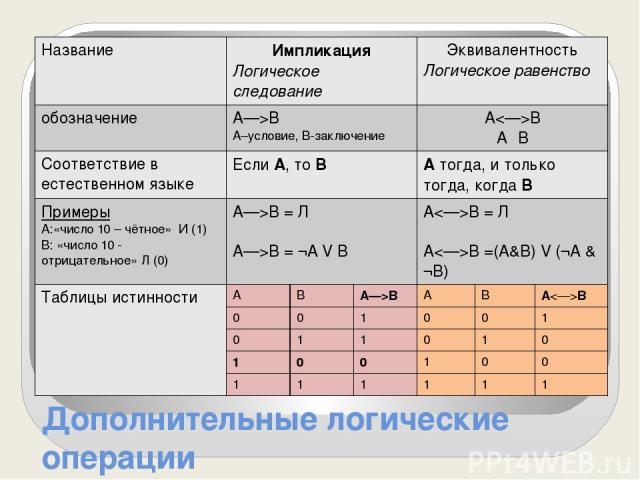
Дополнительные логические операции Название Импликация Логическое следование Эквивалентность Логическое равенство обозначение A—>B А–условие, В-заключение AB AΞB Соответствие в естественномязыке ЕслиА,тоВ Атогда, и толькотогда, когдаВ Примеры А:«число 10 – чётное» И (1) В: «число 10 - отрицательное» Л (0) A—>B= Л A—>B= ¬АVВ AB= Л AB=(A&B)V(¬А&¬В) Таблицы истинности А В A—>B А В AB 0 0 1 0 0 1 0 1 1 0 1 0 1 0 0 1 0 0 1 1 1 1 1 1

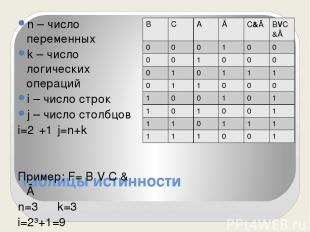
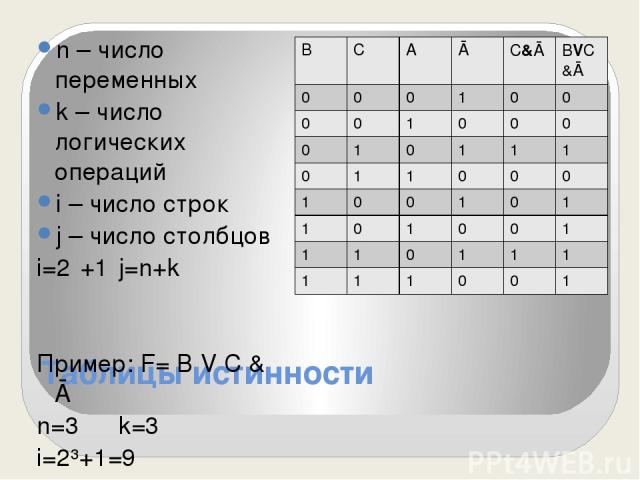
Таблицы истинности n – число переменных k – число логических операций i – число строк j – число столбцов i=2ⁿ+1 j=n+k Пример: F= В V С & Ā n=3 k=3 i=2³+1=9 j=3+3=6 В С А Ā С&Ā ВVС&Ā 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 0 1 0 1 1 0 1 0 0 1 1 1 0 1 1 1 1 1 1 0 0 1

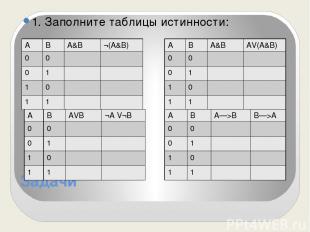
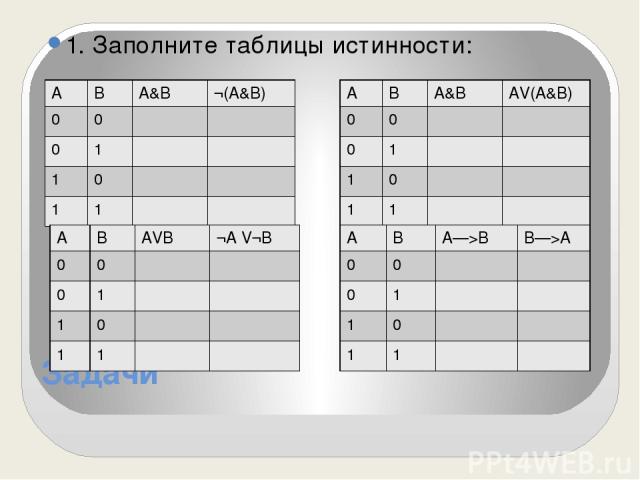
Задачи 1. Заполните таблицы истинности: А В А&В ¬(А&В) 0 0 0 1 1 0 1 1 А В АVВ ¬AV¬B 0 0 0 1 1 0 1 1 А В А&В AV(А&В) 0 0 0 1 1 0 1 1 А В А—>В В—>А 0 0 0 1 1 0 1 1

Задачи 2. Найдите все значения переменных, при которых выражение принимает заданное значение: А V¬B V С = 0 4. Найдите значения логических выражений: F= (0 V 0) V (1 V 1) F=(1 V 1) V (1 V 0) F=(0 & 0) & (1 & 1) 3. Найдите все значения переменных, при которых выражение принимает заданное значение: А & В &¬С = 1 5. Составьте таблицы истинности для выражений: F= (X V ¬Y) & Z F= X & Y V X F= (A V B) & (¬A V ¬B)

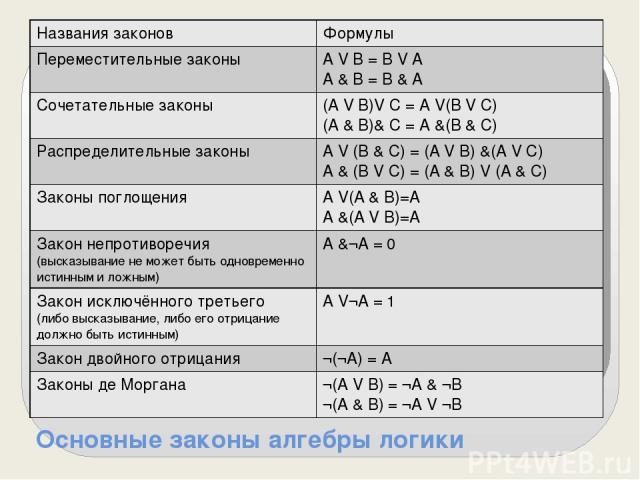
Основные законы алгебры логики Названия законов Формулы Переместительные законы A V B = BV A A & B = B & A Сочетательные законы (A V B)V C = A V(B V C) (A & B)&C = A &(B & C) Распределительные законы A V (B & C) = (A V B) &(A V C) A & (B V C) = (A& B)V (A & C) Законы поглощения A V(A & B)=A A &(A V B)=A Закон непротиворечия (высказывание не может быть одновременно истинным и ложным) A &¬A = 0 Закон исключённого третьего (либо высказывание, либо его отрицание должно быть истинным) A V¬A = 1 Закон двойного отрицания ¬(¬A) = A Законы де Моргана ¬(A V B) =¬A &¬B ¬(A & B) =¬A V¬B

Основные свойства логических операций 6. Докажите равносильность логических выражений с помощью таблиц истинности: A—>B = ¬А V В AB =(A&B) V (¬А & ¬В) 7. Докажите равносильность логических выражений с помощью законов логики: ¬(¬А V ¬В)& С = А & В & С ¬(А V В) & С = ¬А & ¬В & С Конъюнкция Дизъюнкция Импликация А & А = А AVА = А 0—>А = 1 А & 0 = 0 AV0 = А А & 1 = А AV1 = 1

Источники материалов Соколова О.Л. Универсальные поурочные разработки по информатике. 10 класс. М.:ВАКО, 2006. www.vokrugsveta.ru