Презентация на тему: Построение остовного (покрывающего) дерева графа

Построение остовного (покрывающего) дерева графа Преподаватель «И и ИКТ» ГБОУ лицея №1557 Куленчик Олеся Николаевна

Основные определения Остовное дерево – это подграф, не содержащий циклов, включающий все вершины исходного графа, а сумма длин ребер которого минимальна.Цикломатическое число – показывает сколько ребер надо удалить, чтобы в нем не осталось ни одного цикла.

Метод Крускала Ребра исходного графа записываются в порядке возрастания их весов, каждая вершина графа помещается в одноэлементное подмножество. Просматривая ребра исходного графа, делается вывод о включении, либо исключении ребра из остовного дерева. При этом, если ребро связывает вершины, принадлежащие разным подмножествам, то оно включается в остовное дерево, в противном случае ребро удаляется из рассмотрения.

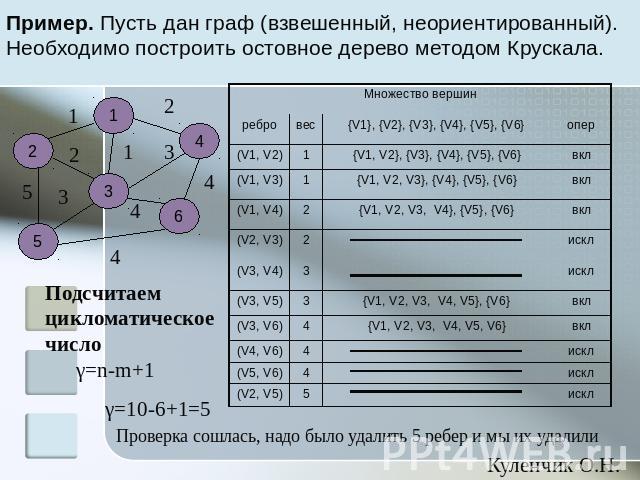
Пример. Пусть дан граф (взвешенный, неориентированный). Необходимо построить остовное дерево методом Крускала. Подсчитаем цикломатическое числоγ=n-m+1 γ=10-6+1=5 Проверка сошлась, надо было удалить 5 ребер и мы их удалили
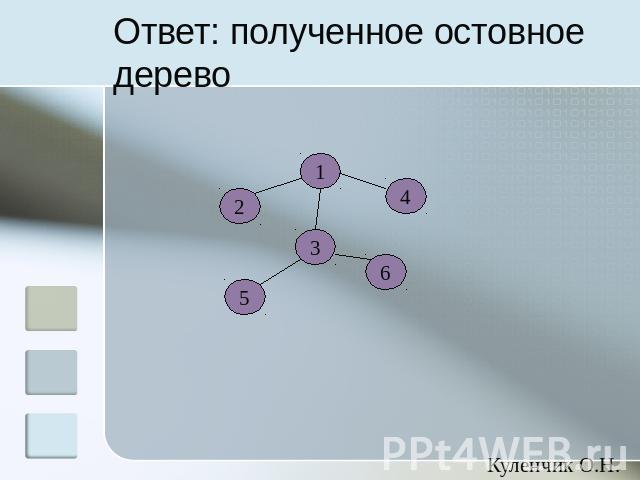
Ответ: полученное остовное дерево

Метод Прима В этом методе первоначально выбирается любая вершина для начального рассмотрения ее по отношению к другим вершинам. После чего, выбирается минимальный вес (с вершиной). Вершину с минимальным весом удаляем из дальнейшего рассмотрения и сносим ее на следующий уровень. Дальше мы начинаем рассматривать снесенную вершину относительно других, оставшихся вершин.

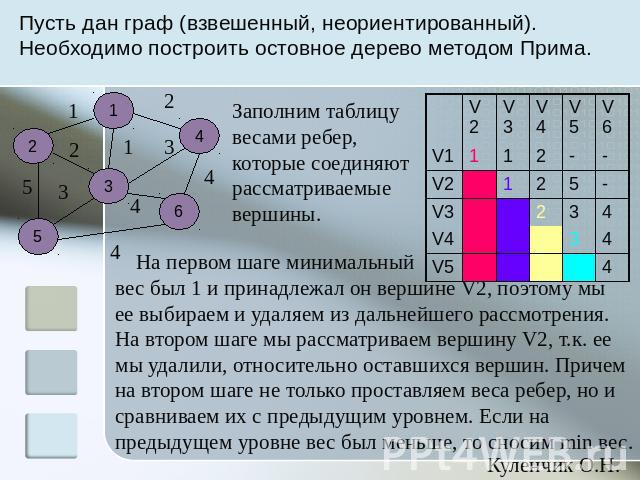
Пусть дан граф (взвешенный, неориентированный). Необходимо построить остовное дерево методом Прима. Заполним таблицувесами ребер, которые соединяютрассматриваемые вершины. На первом шаге минимальныйвес был 1 и принадлежал он вершине V2, поэтому мы ее выбираем и удаляем из дальнейшего рассмотрения. На втором шаге мы рассматриваем вершину V2, т.к. ее мы удалили, относительно оставшихся вершин. Причем на втором шаге не только проставляем веса ребер, но и сравниваем их с предыдущим уровнем. Если на предыдущем уровне вес был меньше, то сносим min вес.

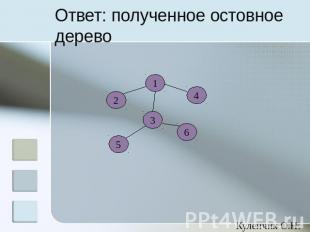
Ответ: полученное остовное дерево Метод построения: Берем последний min вес, он равен 4 и относится квершине V6 что вершину V6 надо соединить в V3,т.к. первый раз 4, в этом столбце, появилось напротив вершины V3. Все оставшиеся вершины соединяются по этому же принципу.