Презентация на тему: Перевод чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую

Система счисления – это способ представления чисел в виде определенного набора цифр.Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на позиционные и непозиционные.Позиционные системы счисления – это такие системы счисления, в которых известно место положения каждой цифры в записи числа относительно запятой. В непозиционных системах счисления запятой нет вообще, поэтому нет позиции цифры. Пример непозиционной системы счисления – римская система счисления.Каждая позиционная система имеет определенный алфавит цифр и основание.

Основание системы счисления в позиционной системе счисления – это количество цифр в алфавите.Алфавит системы счисления – это набор цифр, используемый для записи чисел в этой системе счисления.Позиция цифры в записи числа называется разрядом.

Каждая позиционная система имеет определенный алфавит цифр и основание.

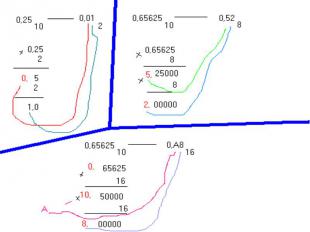
Перевод целых десятичных чисел в двоичный кодЧисло 52810 переведем в двоичную систему счисления.Способ 152810 = 0 * 100 000 + 0 * 10 000 + 5 * 100 + 2 * 10 + 8 * 1Десятичный ряд Как перевести число из десятичной системы в двоичнуюНайти в таблице двоичного ряда самое большое число, которое меньше или равно 528 и отнять его от 528. Это число – 512. 528 – 512 = 162. Найти в таблице двоичного ряда самое большое число, которое меньше или равно 16. Это число 16. 16 – 16 = 0.5. Вписать в таблицу двоичного ряда вместо выбранных чисел – цифру 1, в другие ячейки – цифру 0.

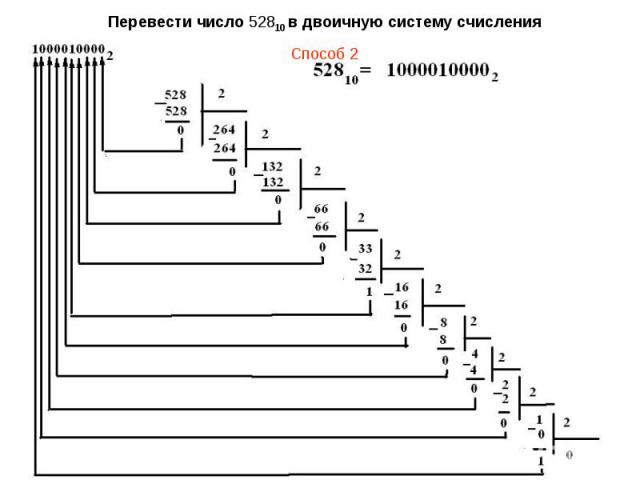
Правило перевода целых десятичных чисел в 2-ю, 8-ю, 16-юсистемы счисления (способ 2)1. Целое десятичное число делят нацело на основание той системы счисления, в которую переводят десятичное число, т. е на 2, 8 или 16 соответственно.2. Остаток от деления записывают как младшую цифру искомого числа.3. Полученное целое частное вновь делят нацело на основание той системы счисления, в которую переводят десятичное число, т. е на 2, 8 или 16 соответственно.4. Остаток от деления записывают слева от предыдущей младшей цифры (см п. 2).4. Процесс деления продолжают до получения целого частного, которое меньше основания системы Примеры представлены на следующем слайде.

Перевести число 52810 в двоичную систему счисленияСпособ 2

Перевод двоичного числа 10000100002 в десятичный кодУмножим попарно цифры двоичного числа с числами двоичного ряда и сложим их.10000100002 = 0 * 2048 + 0 * 1024 + 1 * 512 + 0 * 256 + 0 * 128 + 0 * 64 ++ 0 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 0 * 1 = 52810Ответ 10000100002 = 52810

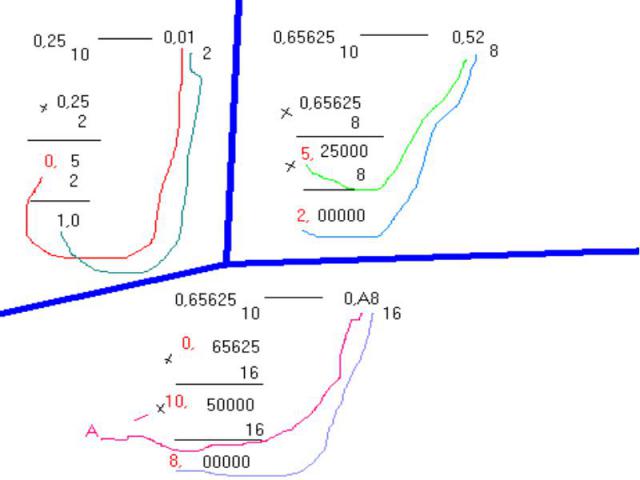
Правило перевода дробных десятичных чисел в 2-й, 8-й, 16-й кодыДробное десятичное число умножают на основание той системы счисления, в которую переводят число, т. е на 2, 8 или 16 соответственно.Целую часть полученного числа записывают как старшую цифру после запятой в той системе счисления, в которую переводят исходное число.Дробную часть полученного числа вновь умножают на основание той системы счисления в которую переводят число, т. е на 2, 8 или 16 соответственно.Пункты 2 и 3 повторяют либо до получения нулевой дробной части, либо до нужной точности знаковПримеры представлены на следующем слайде.

Пример. Перевести число 1011000010001100102 в 8-ю систему счисления. Решение:1. Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:  2. Получаем восьмеричное представление исходного числа: 5410628.  Ответ. 1011000010001100102 = 5410628.

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 8 и обратно   8 = 23Двоичное число разбить справа налево на группы по 3 цифры в каждой. 2. Если в последней левой группе окажется меньше 3-х разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 16 и обратно   16 = 24Двоичное число разбить справа налево на группы по 4 цифры в каждой. 2. Если в последней левой группе окажется меньше 4-х разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

 Пример. Перевести число 10000000001111100001112 в 16-ю систему счисления. Решение.Разбиваем число справа налево в блоки по 4 цифры в каждом.Под каждым блоком записываем соответствующую шестнадцатеричную цифру:  3. Получаем шестнадцатеричное представление исходного числа: 200F8716 Ответ. 10000000001111100001112 = 200F8716.

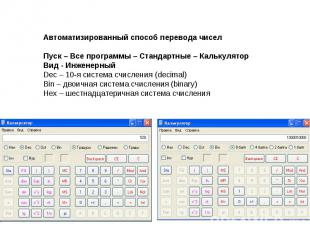
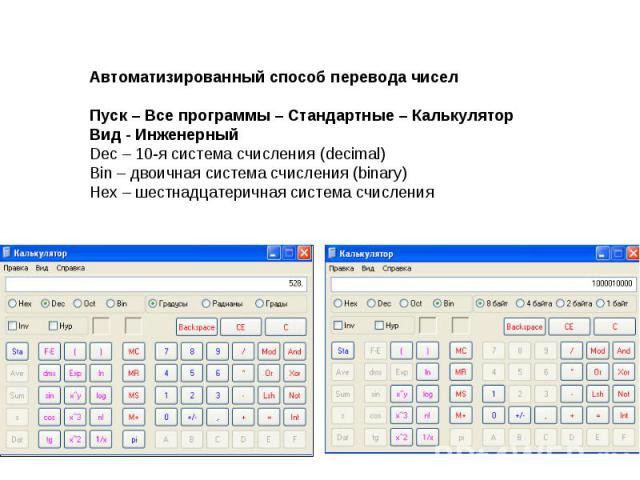
Автоматизированный способ перевода чиселПуск – Все программы – Стандартные – КалькуляторВид - ИнженерныйDec – 10-я система счисления (decimal)Bin – двоичная система счисления (binary)Hex – шестнадцатеричная система счисления