Презентация на тему: Следствия

Следствия

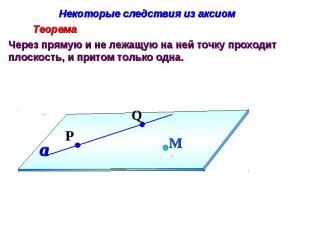
Некоторые следствия из аксиом Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Наглядной иллюстрацией следствия из аксиомы является карандаш лежащий на полу и .

СЛЕДСТВИЯ ИЗ АКСИОМЧерез любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну. Так как М m, то точки А, В и M не принадлежат одной прямой. По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её . Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости .. Таким образом, плоскость проходит через прямую m и точку M и является искомой. Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — , проходящая через прямую m и точку M. Тогда плоскости и проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость единственна. Теорема доказана

СЛЕДСТВИЕ ИЗ Т-1Через две ПАРАЛЛЕЛЬНЫЕ прямые можно провести плоскость, и притом только одну.

Параллельные колонныСтоящие на одной прямой

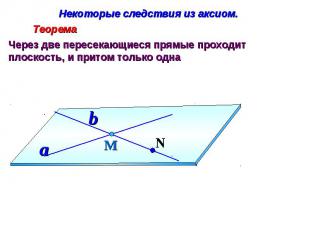
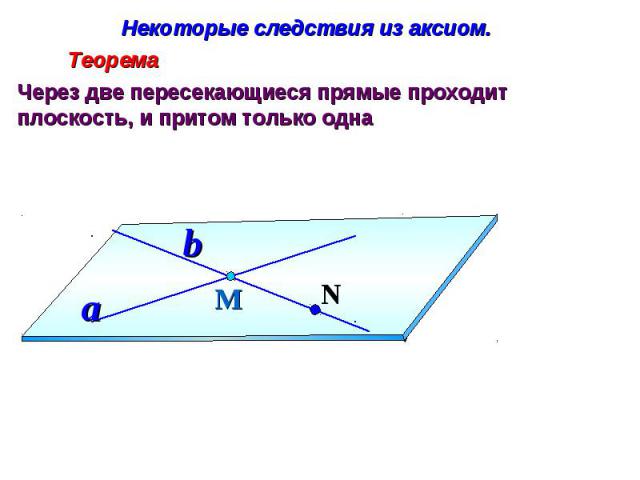
Некоторые следствия из аксиом. Через две пересекающиеся прямые проходит плоскость, и притом только одна

СЛЕДСТВИЯ ИЗ АКСИОМЧерез любые две пересекающиеся прямые можно провести плоскость, и притом только одну. Рассмотрим плоскость =(n, N). Так как M и N , то по А-2 m . Значит обе прямые m, n лежат в плоскости и следовательно , является искомой Докажем единственность плоскости . Допустим, что есть другая, отличная от плоскости и проходящая через прямые m и n, плоскость . Так как плоскость проходит через прямую n и не принадлежащую ей точку N, то по T-1 она совпадает с плоскостью . Единственность плоскости доказана. Теорема доказана