Презентация на тему: симетрія


Якось чужоземець, вражений красою Бухарського мінарету Кальян, вигукнув: “Як ви будуєте такі високі мінарети?” – “Дуже просто”, - відповів Ходжа Якось чужоземець, вражений красою Бухарського мінарету Кальян, вигукнув: “Як ви будуєте такі високі мінарети?” – “Дуже просто”, - відповів Ходжа


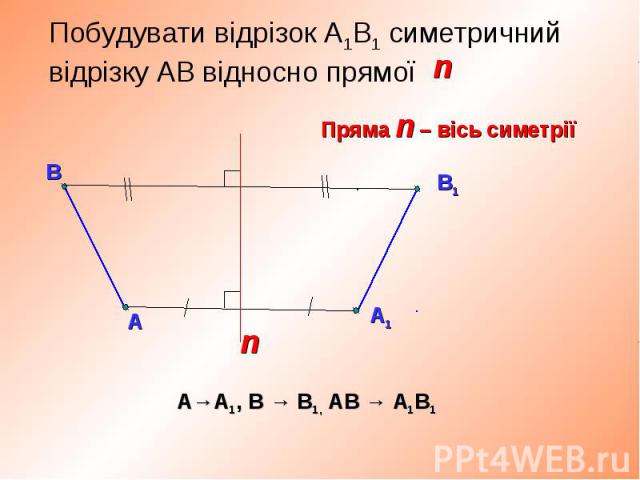
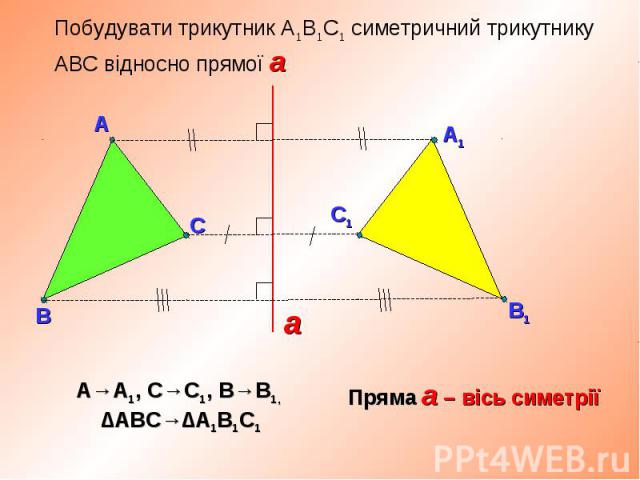
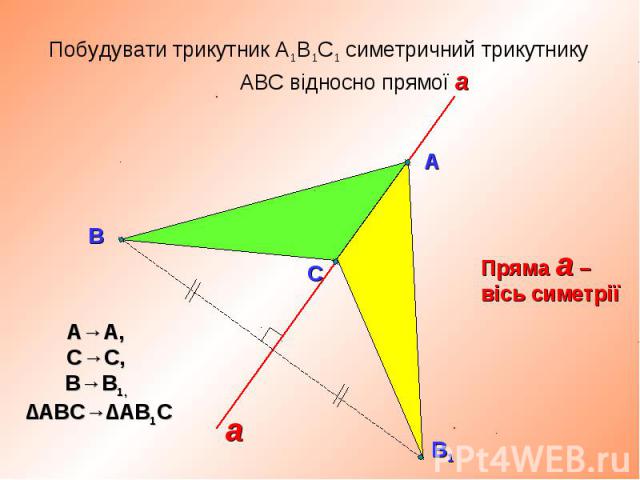
Назвіть точки, симетричні відносно прямої g. Назвіть точки, симетричні відносно прямої g.

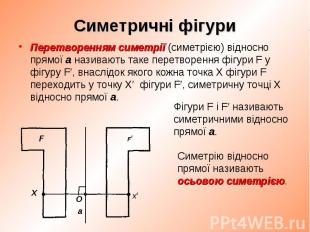
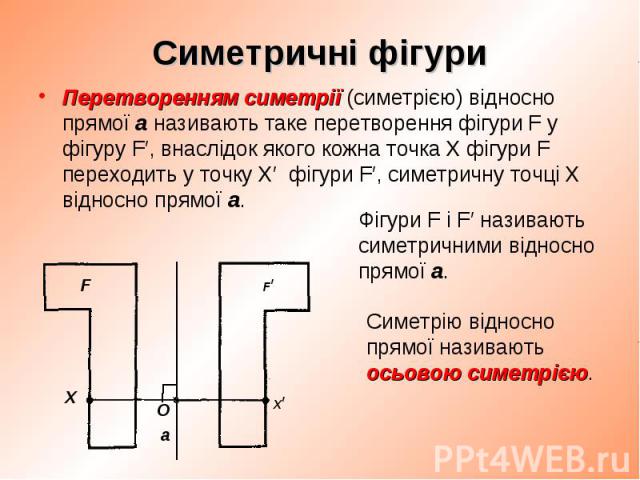
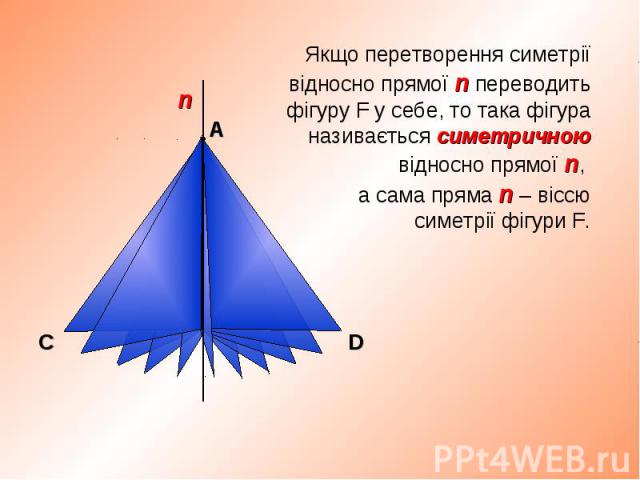
Перетворенням симетрії (симетрією) відносно прямої a називають таке перетворення фігури F у фігуру F′, внаслідок якого кожна точка Х фігури F переходить у точку Х′ фігури F′, симетричну точці Х відносно прямої a. Перетворенням симетрії (симетрією) відносно прямої a називають таке перетворення фігури F у фігуру F′, внаслідок якого кожна точка Х фігури F переходить у точку Х′ фігури F′, симетричну точці Х відносно прямої a.
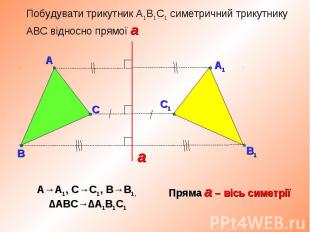
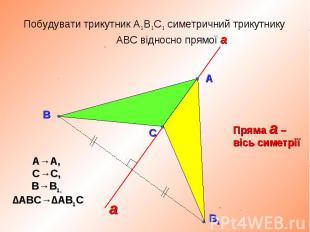
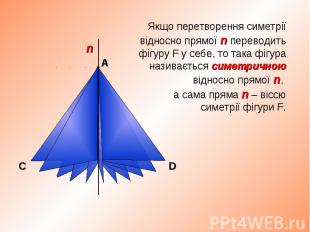
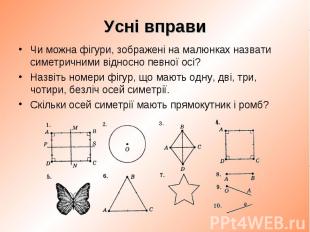
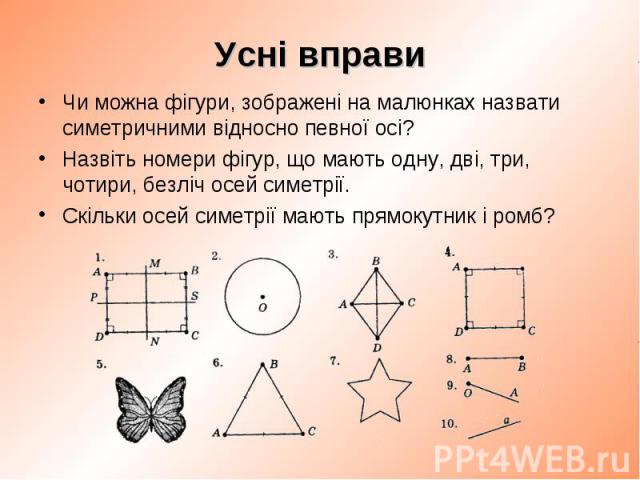
Чи можна фігури, зображені на малюнках назвати симетричними відносно певної осі? Чи можна фігури, зображені на малюнках назвати симетричними відносно певної осі? Назвіть номери фігур, що мають одну, дві, три, чотири, безліч осей симетрії. Скільки осей симетрії мають прямокутник і ромб?

Доведення. Доведення. Осьова симетрія відносно прямої n: точка Х – переходить в точку Х′, точка Y переходить у точку Y′. n=Оу. Тоді: Х (х1;у1)→Х′(-х1;у1), Y(х2;у2)→Y′(-х2;у2).

1) Перетворення осьової симетрії є переміщенням. 2) Осьова симетрія перетворює пряму на пряму; відрізок – на відрізок; многокутник – на рівний йому многокутник. 3)Точки, що належать осі симетрії, відображаються самі на себе. 4)Якщо точки М(х;у) і N(х1; у1) симетричні відносно: А) осі Ох, то виконується умова: х1=х, у1=-у; Б) осі Оу, то виконується умова х1=-х, у1=у.

Які точки називаються симетричними відносно прямої? Яке перетворення називається симетрією відносно даної прямої? Яка фігура називається симетричною відносно даної прямої? Що таке вісь симетрії? Наведіть приклади.