Презентация на тему: Жидкость

Лекция 10 Тема: ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД Упругие напряжения и деформации. Закон Гука. Общие свойства жидкостей и газов. 3. Поток вектора скорости. Уравнение непрерывности. 4. Циркуляция векторного поля. Ротор вектора. Уравнения движения и равновесия жидкости. 5. Уравнение движения и равновесия жидкости. 6. Стационарное движение идеальной жидкости. Уравнение Бернулли. 7. Стационарное течение вязкой жидкости. Содержание лекции: Сегодня: * 900igr.net

1. Упругие напряжения и деформации. Закон Гука

Идеально (абсолютно) упругим телом называется такое тело, которое обладает свойством восстанавливать свои размеры и форму после того, как деформирующие его силы прекращают свое воздействие. Рассматриваем не сам процесс деформирования, а конечный результат, после установления равновесия в деформируемом теле. Рассмотрим некоторое тело, деформированное внешними силами. Внешние силы вызывают смещения частиц тела по сравнению с исходным состоянием. В результате в теле возникают внутренние силы, т.е. тело переходит в напряженное состояние.

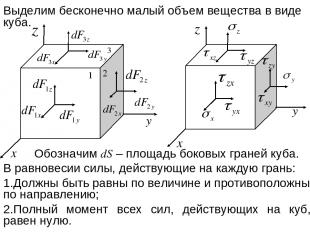
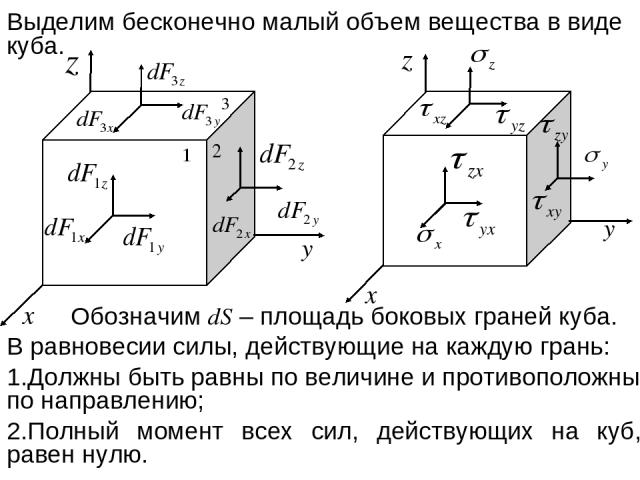
Выделим бесконечно малый объем вещества в виде куба. Обозначим dS – площадь боковых граней куба. В равновесии силы, действующие на каждую грань: Должны быть равны по величине и противоположны по направлению; Полный момент всех сил, действующих на куб, равен нулю.

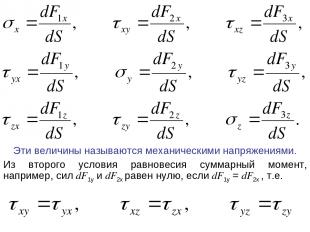
Эти величины называются механическими напряжениями. Из второго условия равновесия суммарный момент, например, сил dF1y и dF2x равен нулю, если dF1y = dF2x , т.е.

Компоненты - нормальные напряжения, в зависимости от знака характеризуют растягивающие (сжимающие) усилия. Напряжения - касательные (сдвиговые) напряжения, действуют в плоскости соответствующих граней. При внешнем воздействии в общем случае тело изменяет свои размеры и форму, т.е. испытывает деформацию. При всем разнообразии деформаций оказывается возможным любую из них свести к двум. Элементарными деформациями являются растяжение (сжатие) и сдвиг.

Деформация растяжения (сжатия) – характеризуют величиной относительного удлинения. Если выделенный в теле объем до действия сил имел длину l в некотором направлении, а после приложения сил, эта длина изменилась на l, то относительное удлинение будет При растяжении >0, при сжатии

Деформация сдвига характеризуется величиной относительного сдвига Закон Гука Относительное растяжение (сжатие) пропорционально растягивающему (сжимающему) напряжению . Е – модуль Юнга – напряжение, создающее относительное удлинение тела, равное единице.

Растяжение, например, стержня, сопровождается его поперечным сжатием. - относительное сжатие. Относительное сжатие связано с относительным растяжением: - коэффициент Пуассона. «-» – отражает тот факт, что продольная и поперечная деформации при одноосном растяжении (сжатии) всегда имеют противоположные знаки.

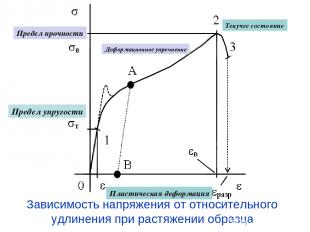
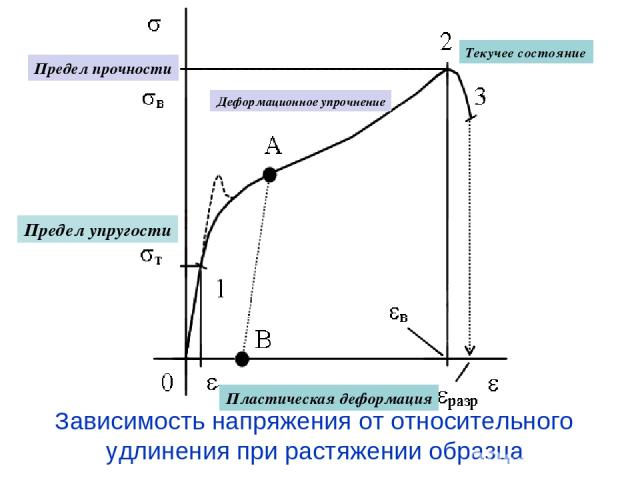
Зависимость напряжения от относительного удлинения при растяжении образца Предел упругости Пластическая деформация Деформационное упрочнение Предел прочности Текучее состояние

2. Общие свойства жидкостей и газов

Агрегатное состояния вещества Твердое Жидкое Газообразное Зависит от соотношения между потенциальной энергией взаимодействия атомов Wвз, составляющих тело, и их средней кинетической энергией Wср.кин. Wвз >> Wср.кин, твердое состояние. Wвз Wср.кин, жидкое состояние. Wвз

Способы кинематического описания жидкостей Способ Лагранжа. Выбирается совокупность «жидких» частиц, движение жидкости описывается как движение таких частиц. Вводится понятие скорости и ускорения частиц (трудно учесть изменение формы «жидкой» частицы при движении). Способ Эйлера. Задается векторное поле скоростей движения жидкости, т.е. фиксируем, как ведет себя скорость течения жидкости в точках ее объема с течением времени. Следим за кинематическими характеристиками жидкости в фиксированных точках пространства, не интересуясь тем, какие именно «жидкие» частицы проходят эти точки. Для наглядного представления вводят линии тока.

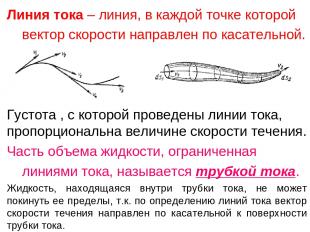
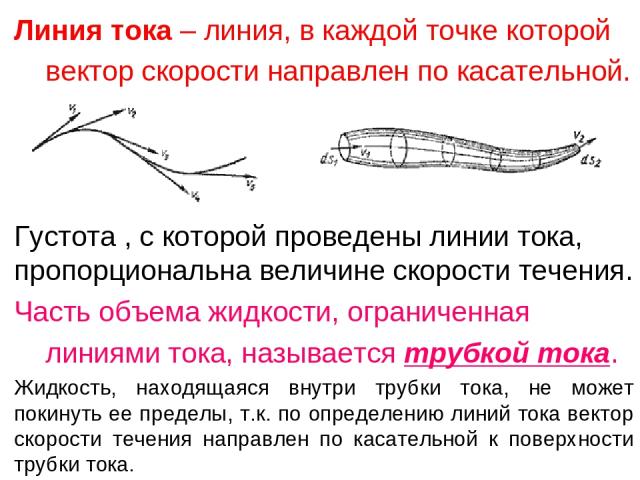
Линия тока – линия, в каждой точке которой вектор скорости направлен по касательной. Густота , с которой проведены линии тока, пропорциональна величине скорости течения. Часть объема жидкости, ограниченная линиями тока, называется трубкой тока. Жидкость, находящаяся внутри трубки тока, не может покинуть ее пределы, т.к. по определению линий тока вектор скорости течения направлен по касательной к поверхности трубки тока.

3. Поток вектора скорости; уравнение непрерывности

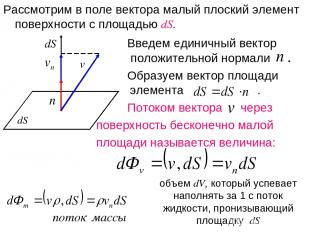
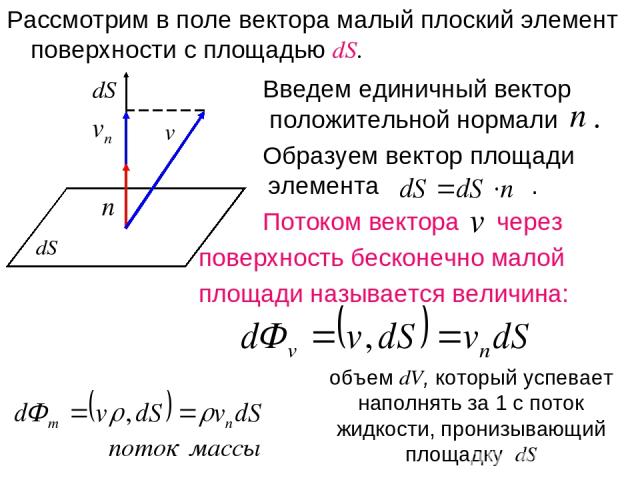
Рассмотрим в поле вектора малый плоский элемент поверхности с площадью dS. Введем единичный вектор положительной нормали . Образуем вектор площади элемента . Потоком вектора через поверхность бесконечно малой площади называется величина: объем dV, который успевает наполнять за 1 с поток жидкости, пронизывающий площадку dS

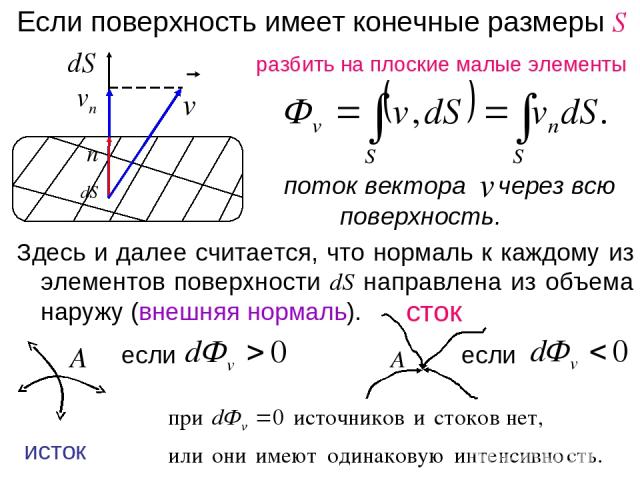
Если поверхность имеет конечные размеры S разбить на плоские малые элементы поток вектора через всю поверхность. Здесь и далее считается, что нормаль к каждому из элементов поверхности dS направлена из объема наружу (внешняя нормаль). если исток сток если

Рассмотрим в поле вектора малый объем V, окруженный замкнутой поверхностью S. Тогда будет характеризовать общую интенсивность источников и стоков, находящихся в объеме V. характеризует удельную интенсивность источников (стоков). Это локальная удельная характеристика интенсивности источников жидкости в точке А поля .

Если div(v) = 0, в т. А нет источников (стоков). Если div(v) > 0, т. А является источником. Если div(v) < 0, т. А является стоком. Чем больше div(v) > 0, тем выше интенсивность источника. Это локальная удельная характеристика интенсивности источников жидкости в точке А поля .

Уравнение непрерывности Выберем в жидкости объем V, ограничим замкнутой поверхностью S. Поток массы через S: Масса жидкости, заключенной внутри S, равна В отсутствие источников (стоков) жидкости внутри объема масса жидкости, которая вытекает из него, должна быть равна изменению массы объема V в единицу времени, т.е. .

Уравнение непрерывности жидкости в интегральной форме. Если течение стационарно, т.е. величины, характеризующие течение жидкости, не зависят явно от времени, то Смысл: в стационарном потоке сколько жидкости входит в данный объем, столько и выходит из него.

4. Циркуляция векторного поля. Ротор вектора. Уравнения движения и равновесия жидкости.

Пусть в поле скоростей v (x, y, z) задана некоторая кривая L. Разобьем эту кривую на малые векторные элементы dl, направление которых совпадает с направлением обхода L. циркуляция вектора скорости вдоль кривой L (характеризует завихренность поля вектора в области расположения L).

Это локальная характеристика завихренности потока жидкости в окрестности точки А.

В жидкости отсутствует понятие сдвига. В жидкости могут быть только напряжения всестороннего сжатия, причем где Р – давление – сила, действующая на некоторую площадку, помещенную в жидкость перпендикулярно силе и отнесенной к единице площади:

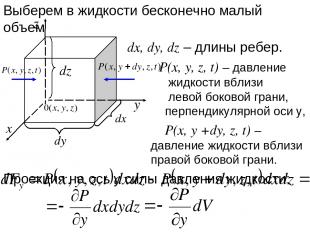
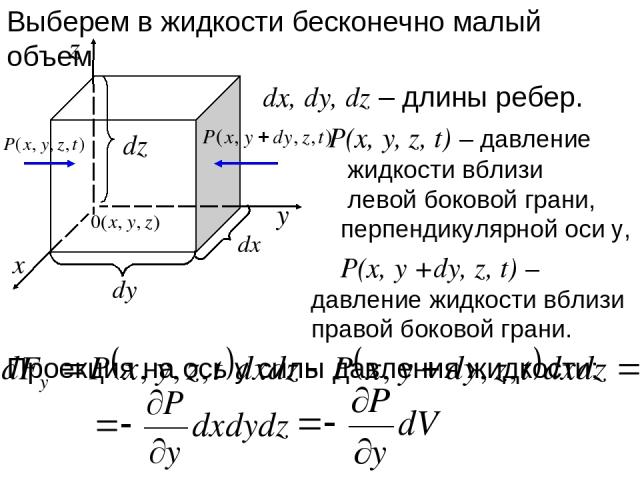
Выберем в жидкости бесконечно малый объем dx, dy, dz – длины ребер. P(x, y, z, t) – давление жидкости вблизи левой боковой грани, перпендикулярной оси y, P(x, y +dy, z, t) – давление жидкости вблизи правой боковой грани. Проекция на ось y силы давления жидкости:

Воспользуемся определением частной производной , т е. проекция силы давления, отнесенная к единице объема: Аналогично: Сила давления, действующая на элемент жидкости. Учтем, что жидкость может находиться в гравитационном поле, потенциал которого , тогда - сила, действующая со стороны этого поля на единицу массы. -сила, отнесенная к единице объема.

Идеальная жидкость – жидкость, вязкостью которой можно пренебречь. Запишем второй закон Ньютона Уравнение движения идеальной жидкости в гравитационном поле В равновесии справедлив закон Паскаля: давление, оказываемое на жидкость, передается ею по всем направлениям одинаковым образом.

Частный случай: несжимаемая жидкость. Жидкость находится в однородном поле тяготения. Выберем положительное направление оси z вертикально верх. Тогда потенциал будет где g – ускорение свободного падения. Подставим в уравнение равновесия: линейное увеличение гидростатического давления с увеличением глубины

Одно из проявлений закона Паскаля можно наблюдать в гидравлическом прессе: два сообщающихся сосуда заполнены жидкостью и закрыты поршнями различной площади. По закону Паскаля, давления под поршнями одинаковы: Таким образом, сила давления второго поршня больше силы давления первого во столько раз, во сколько площадь больше первого. Гидравлический пресс – простой механизм, позволяющий развить колоссальные силы, используемые для прессования различных изделий из металлов и пластмасс. Обозначим - ходы поршней.

Вследствие несжимаемости объемы жидкости, перешедшего из одного цилиндра в другой, одинаковы: Работы, совершаемые силами за один ход Их отношение Как и следовало ожидать, пресс дает выигрыш в силе, но не в совершаемой работе.

Согласно формуле Сила давления на нижние слои жидкости будет больше, чем на верхние. Поэтому на тело, погруженное в жидкость, действует выталкивающая сила – сила Архимеда. Погрузим в жидкость на глубину h параллелепипед с площадью основания S и высотой ребра a. Давление на глубине h равно

Поэтому на верхнее основание действует сила На глубине h + a давление равно Поэтому на нижнее основание действует сила Равнодействующая этих двух сил направлена вверх и равна по величине Здесь - объем погруженной части тела, - масса жидкости (газа) того же объема. Закон Архимеда: на тело погруженное в жидкость (газ), действует выталкивающая сила, равна весу вытесненной телом жидкости (газа).

6. Стационарное движение идеальной жидкости. Уравнение Бернулли

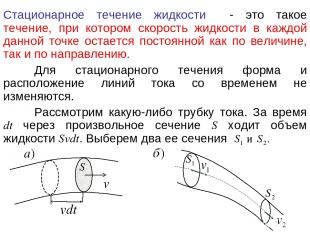
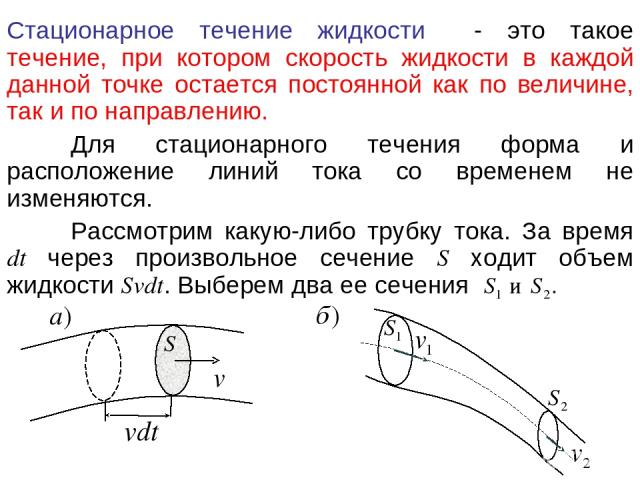
Стационарное течение жидкости - это такое течение, при котором скорость жидкости в каждой данной точке остается постоянной как по величине, так и по направлению. Для стационарного течения форма и расположение линий тока со временем не изменяются. Рассмотрим какую-либо трубку тока. За время dt через произвольное сечение S ходит объем жидкости Svdt. Выберем два ее сечения

За время dt через сечение пройдет объем жидкости Аналогично, через сечение за то же время dt пройдет объем Из условия несжимаемости жидкости следует равенство объемов, вошедших в область между сечениями и вышедших из нее: Следовательно, для несжимаемой жидкости величина Sv в любом сечении одной и той же трубки тока одинакова: Sv = const. – теорема о непрерывности струи. Примечание: Теорема применима к реальным жидкостям и газам, если их сжимаемостью можно пренебречь. Следствие: в месте сужения трубы скорость потока возрастает.

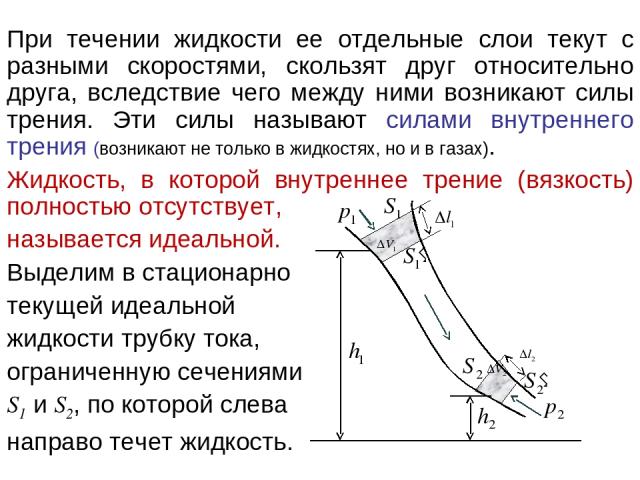
При течении жидкости ее отдельные слои текут с разными скоростями, скользят друг относительно друга, вследствие чего между ними возникают силы трения. Эти силы называют силами внутреннего трения (возникают не только в жидкостях, но и в газах). Жидкость, в которой внутреннее трение (вязкость) полностью отсутствует, называется идеальной. Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость.

За время Δt объем жидкости переместится вдоль трубки тока. В силу непрерывности струи заштрихованные объемы будут иметь одинаковую величину: Энергия каждой частицы жидкости Полная энергия потока, протекающего за Δt через сечение S1 Аналогично для S2

Изменение полной механической энергии Силы давления на боковую поверхность трубки тока перпендикулярны в каждой точке к направлению перемещения частиц, поэтому работу не совершают. Отлична от нуля только работа сил, приложенных к сечениям S1 и S2.

Сечения S1 и S2 были взяты произвольно. Поэтому в стационарно текущей идеальной жидкости в любом сечении трубки выполняется условие: Уравнение Бернулли: в установившемся движении идеальной жидкости полное давление, слагающееся из динамического, гидростатического и статического, одинаково для всех поперечных сечений трубки тока.

7. Движение тел в среде с сопротивлением. Стационарное течение вязкой жидкости

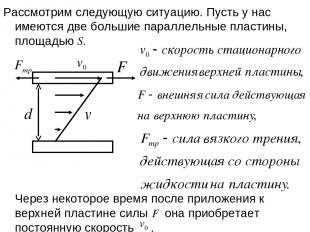
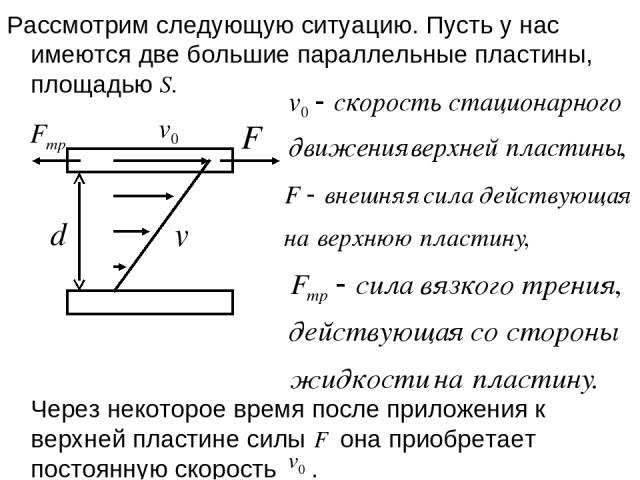
Рассмотрим следующую ситуацию. Пусть у нас имеются две большие параллельные пластины, площадью S. Через некоторое время после приложения к верхней пластине силы она приобретает постоянную скорость .

Слои жидкости также станут двигаться, причем величина скорости этих слоев будет линейно возрастать от 0 до с увеличением расстояния от нижней пластины. Выводы: 1. Вязкая жидкость «прилипает» к поверхности твердого тела. Скорость жидкости на поверхности тела и скорость тела движущегося в жидкости одинаковы (условие «прилипания»). 2. Так как скорость постоянна, то со стороны жидкости на верхнюю пластину действует сила, которая компенсирует внешнюю силу . Это и есть сила вязкого трения . Она действует не только на твердые тела в жидкости, но и между элементами самой жидкости.

Для величины силы вязкого трения в условиях рассматриваемого опыта справедливо равенство Формула Ньютона - коэффициент вязкости – динамическая вязкость Уравнение движения вязкой жидкости – уравнение Навье-Стокса Применяется для описания движения реальных жидкостей и газов

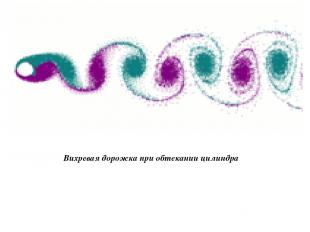
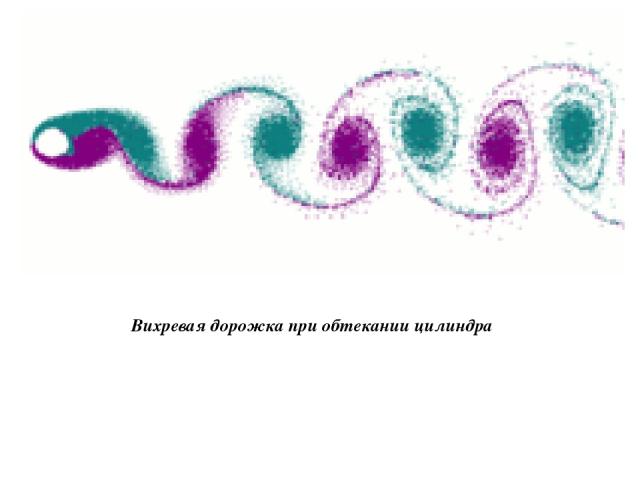
Вихревая дорожка при обтекании цилиндра

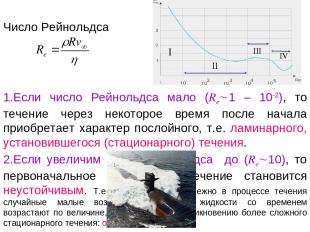
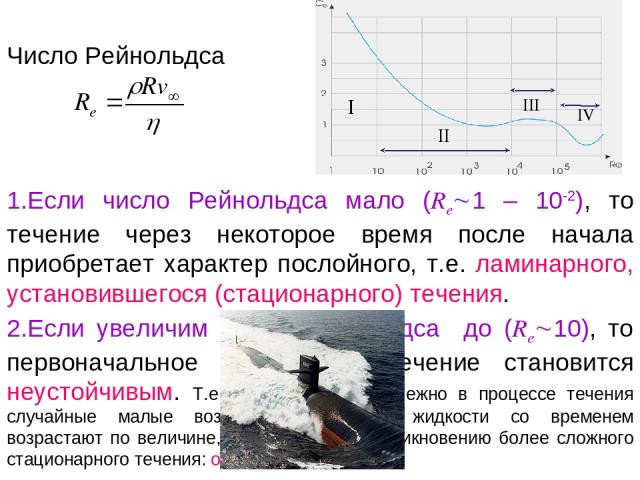
Число Рейнольдса Если число Рейнольдса мало (Re 1 – 10-2), то течение через некоторое время после начала приобретает характер послойного, т.е. ламинарного, установившегося (стационарного) течения. Если увеличим число Рейнольдса до (Re 10), то первоначальное ламинарное течение становится неустойчивым. Т.е. возникающие неизбежно в процессе течения случайные малые возмущения скорости жидкости со временем возрастают по величине, что приводит к возникновению более сложного стационарного течения: образуются два вихря.

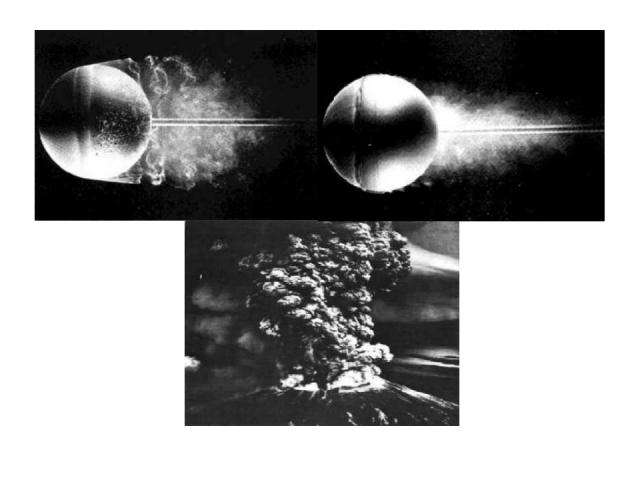
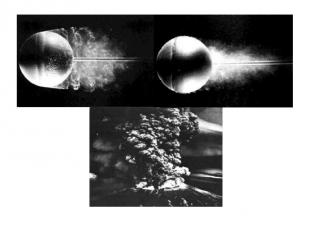
3. Если увеличить число Рейнольдса до (Re 102), то характер течения снова меняется за счет нового типа неустойчивости: возникает нестационарное обтекание, при котором вихри отрываются и уносятся по течению. 4. Если увеличить число Рейнольдса до (Re 104-105), течение становится полностью неупорядоченным, хаотическим. Такое течение называет турбулентным.

Ламинарное (на переднем плане) и турбулентное течение вокруг субмарины «Лос-Анджелес»

Лекция окончена Нажмите клавишу для выхода