Презентация на тему: Закон Ньютона физика

Решение задач по теме «Законы Ньютона» Цель урока: 1. Знать алгоритм решения задач на законы Ньютона. 2. Уметь применять алгоритм к решению задач на законы Ньютона. 900igr.net

Повторим теорию В чем состоит основное утверждение механики? Что в физике понимают под материальной точкой? Сформулируйте первый закон Ньютона. Приведите примеры, объясняющие данную формулировку.

Повторим теорию 4. Что в физике понимают под термином «сила»? 5. Приведите примеры, показывающие связь сила и ускорения, с которым движется тело. 6. Сформулируйте второй закон Ньютона и запишите его математическое выражение. 7. В чем состоит третий закон Ньютона? Запишите его математическое выражение. Поясните на примерах смысл этого закона. Каковы особенности сил, о которых идет речь в третьем законе Ньютона?

Повторим теорию Какие системы отсчета называются инерциальными? Неинерциальными? Привести примеры. В чем состоит принцип относительности в механике? Кто открыл этот принцип?

Основная задача механики Нахождение положения и скорости тела в любой момент времени, если известны его положение и скорость в начальный момент времени и действующие на него силы. (Прямая задача) Определение сил по известному или заданному движению.

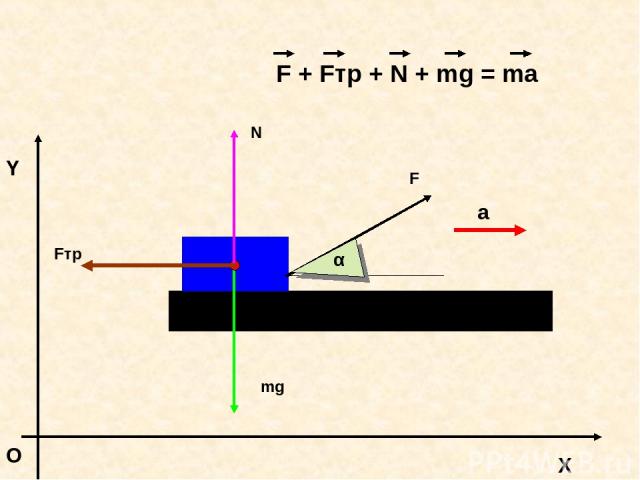
Алгоритм решения задач Понять предложенную задачу (увидеть физическую модель). Анализ (построить математическую модель явления): Выбрать систему отсчета. Найти все силы, действующие на тело, и изобразить их на чертеже. Определить (или предположить) направление ускорения и изобразить его на чертеже. Записать уравнение второго закона Ньютона в векторной форме и перейти к скалярной записи, заменив все векторы их проекциями на оси координат. Исходя из физической природы сил, выразить силы через величины, от которых они зависят. Если в задаче требуется определить положение или скорость точки, то к полученным уравнениям динамики добавить кинетические уравнения. Полученную систему уравнений решить относительно искомой величины. Решение проверить и оценить критически.

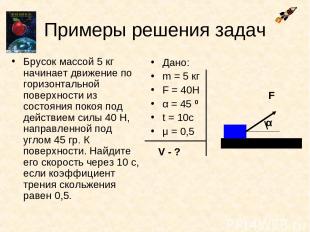
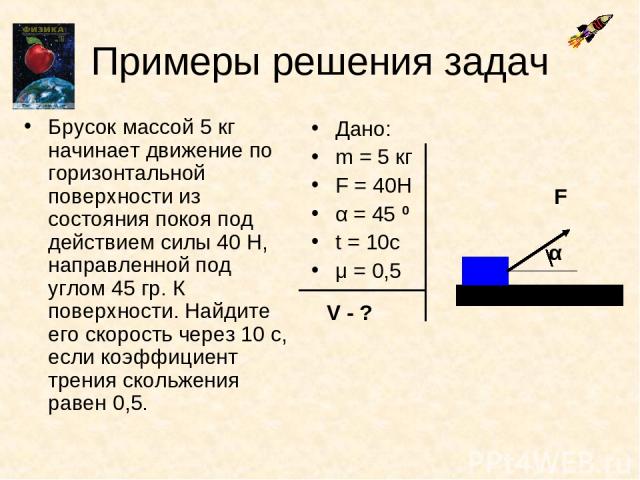
Примеры решения задач Брусок массой 5 кг начинает движение по горизонтальной поверхности из состояния покоя под действием силы 40 Н, направленной под углом 45 гр. К поверхности. Найдите его скорость через 10 с, если коэффициент трения скольжения равен 0,5. Дано: m = 5 кг F = 40Н α = 45 0 t = 10с μ = 0,5

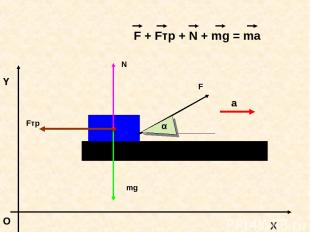
O

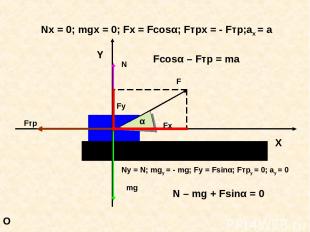
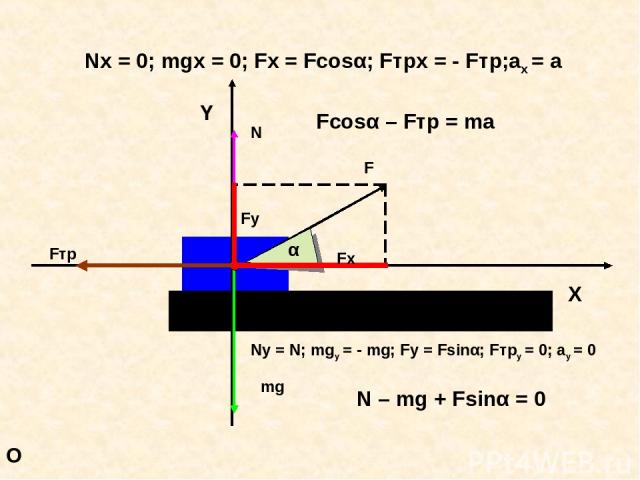
O Nx = 0; mgx = 0; Fx = Fcosα; Fтрx = - Fтр;ax = a Fcosα – Fтр = ma Ny = N; mgy = - mg; Fy = Fsinα; Fтрy = 0; ay = 0 N – mg + Fsinα = 0

1. Скалярная форма записи Fcosα – Fтр = ma N – mg + Fsinα = 0 2. Выразить силы через величины, от которых они зависят Fтр = μ N 3. Добавить кинематические уравнения: Vx = V0 + at 4. Полученную систему уравнений решить относительно искомой величины.

Решение системы уравнений относительно а Fcosα – Fтр = ma N – mg + Fsinα = 0 Fтр = μ N Vx = V0 + at Fcosα - μ N = ma N = mg - Fsinα Fcosα – μ(mg - Fsinα ) = ma

Нахождение искомой величины V = m [Fcosα – μ(mg - Fsinα )] t a t = Вычислить искомую величину