Презентация на тему: Закон Гука

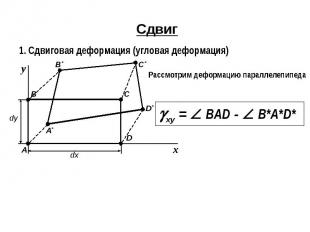
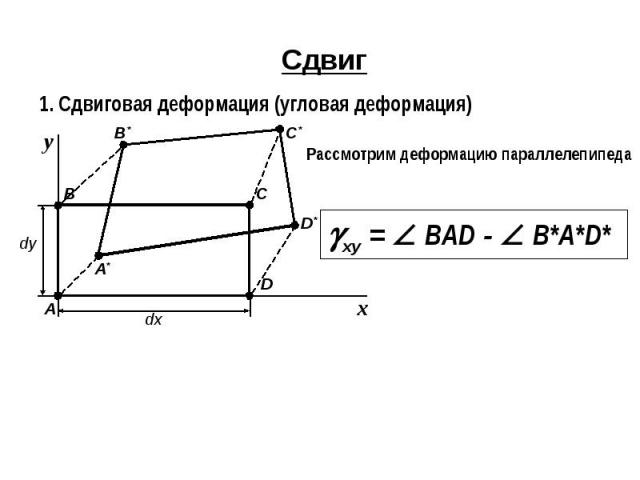
Сдвиг1. Сдвиговая деформация (угловая деформация)Рассмотрим деформацию параллелепипеда

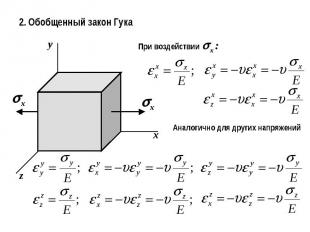
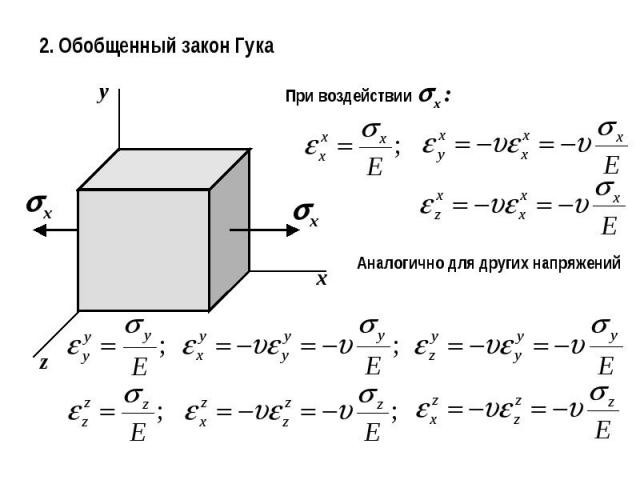
2. Обобщенный закон ГукаПри воздействии x :Аналогично для других напряжений

2. Обобщенный закон ГукаИспользуя принцип суперпозиции:Обобщенный закон Гука для изотропного тела

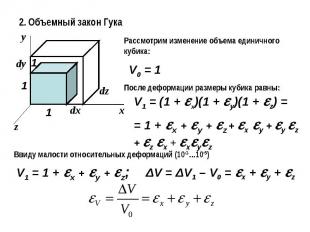
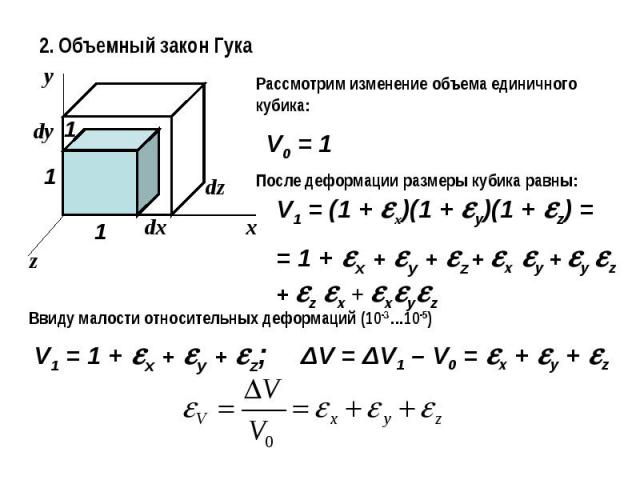
2. Объемный закон ГукаРассмотрим изменение объема единичного кубика:После деформации размеры кубика равны:Ввиду малости относительных деформаций (10-3…10-5)

2. Объемный закон ГукаИспользуем обобщенный закон Гука:Объемный закон ГукаОбозначим:- среднее напряжениеТогда:Обозначим:- объемный модуль упругостиВидно, что nпред = 0.5

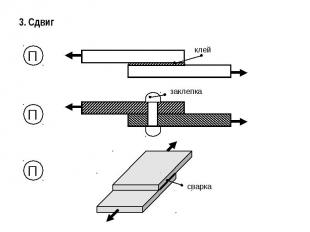
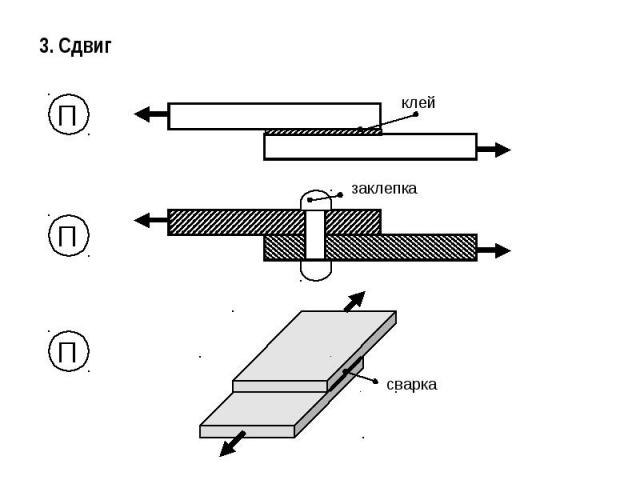
3. Сдвиг

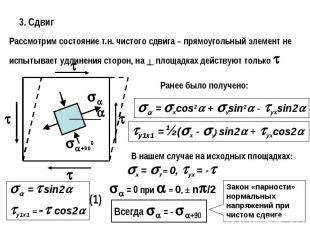
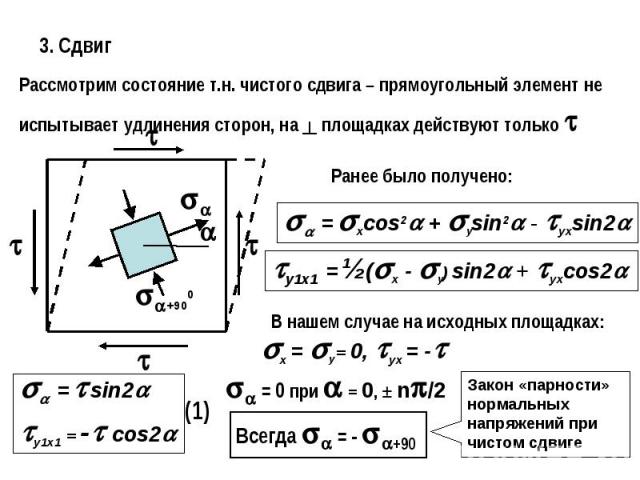
3. СдвигРассмотрим состояние т.н. чистого сдвига – прямоугольный элемент не испытывает удлинения сторон, на ┴ площадках действуют только Ранее было получено:В нашем случае на исходных площадках:Закон «парности» нормальных напряжений при чистом сдвиге

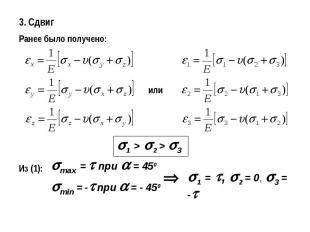
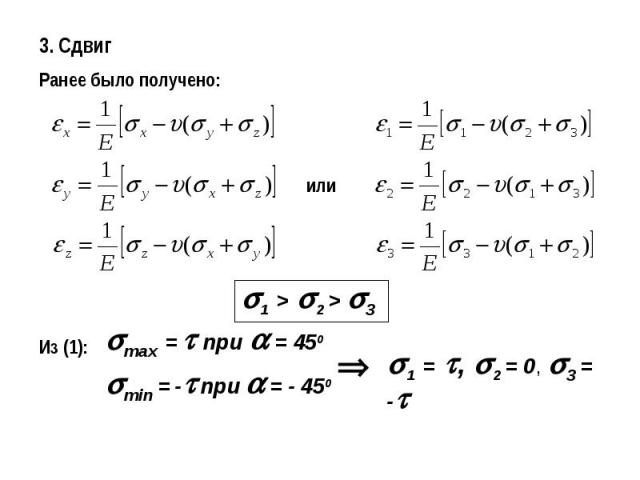
3. СдвигРанее было получено:

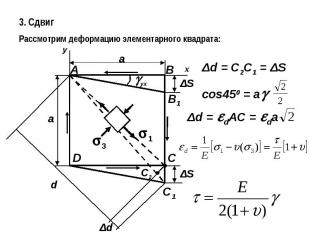
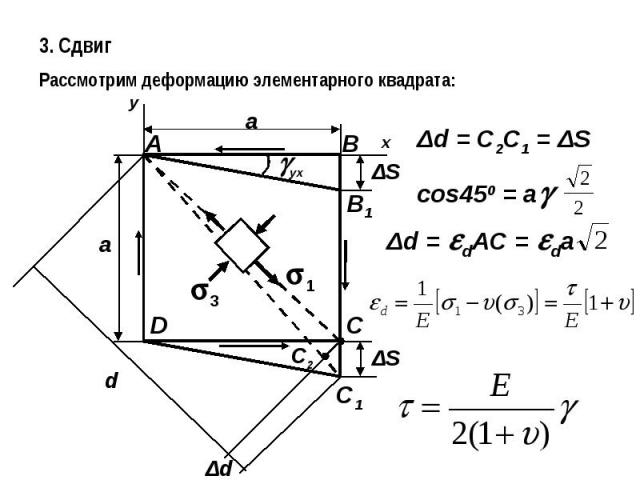
3. СдвигРассмотрим деформацию элементарного квадрата:

3. СдвигРассмотрим аналогию:- модуль сдвига или «модуль упругости второго рода»

3. СдвигПолная сводка уравнений для пространственного напряженного состояния:

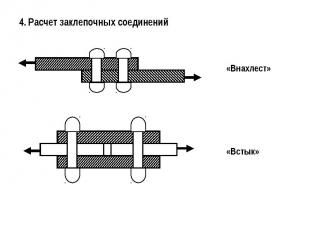
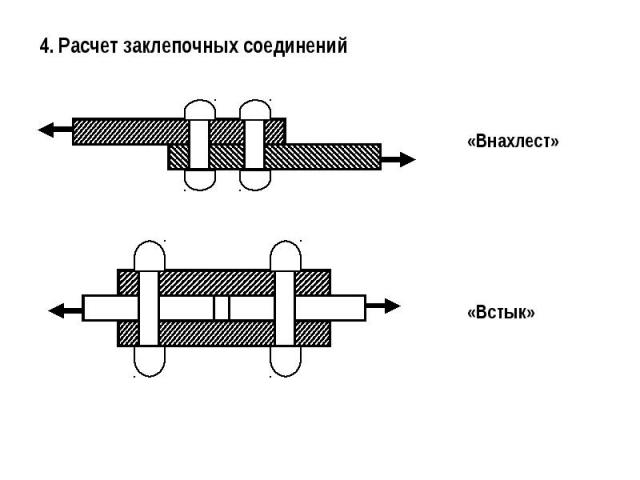
4. Расчет заклепочных соединений

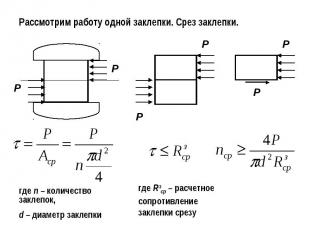
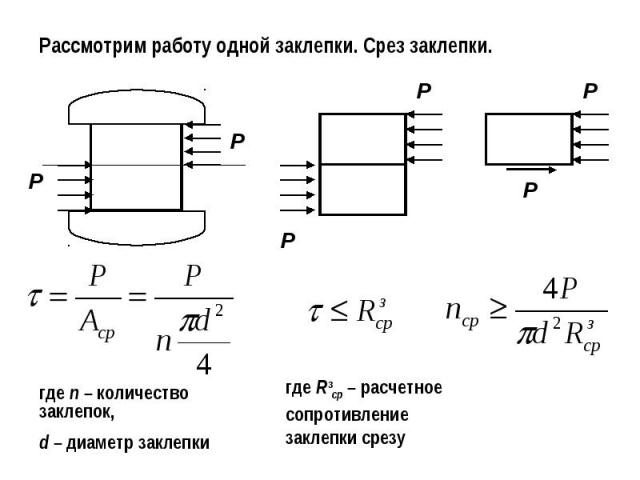
Рассмотрим работу одной заклепки. Срез заклепки.где n – количество заклепок,d – диаметр заклепкигде Rзср – расчетное сопротивление заклепки срезу

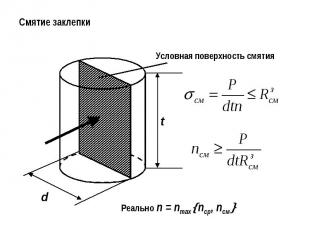
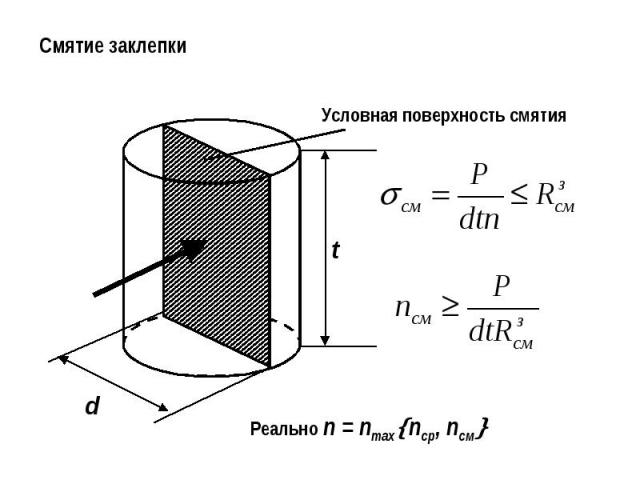
Смятие заклепкиУсловная поверхность смятияРеально n = nmaxnср, nсм

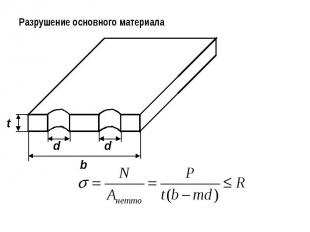
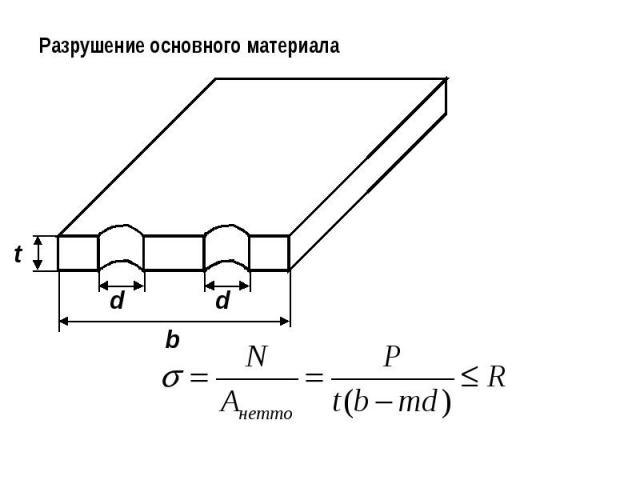
Разрушение основного материала

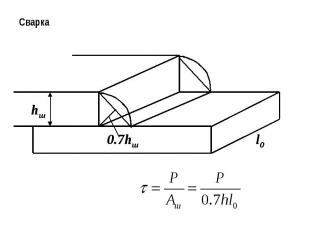
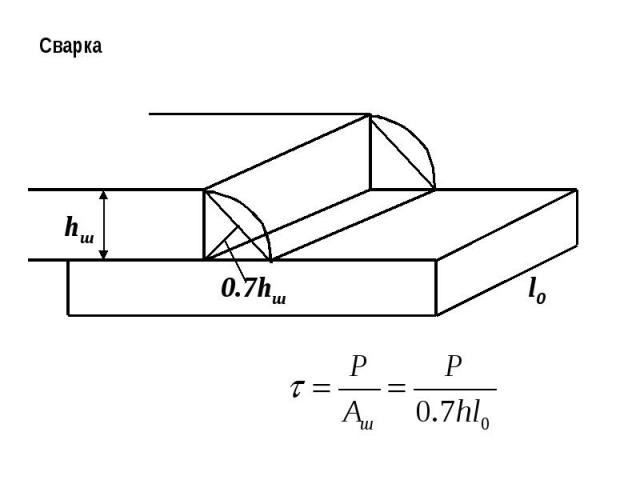
Сварка