Презентация на тему: Теорема Гаусса (закон Гаусса)

* Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.

* Суммарный электрический поток через произвольную замкнутую поверхность Закон Гаусса

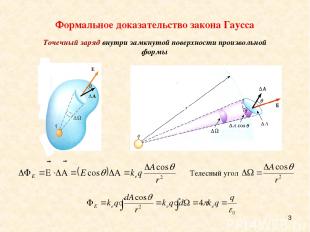
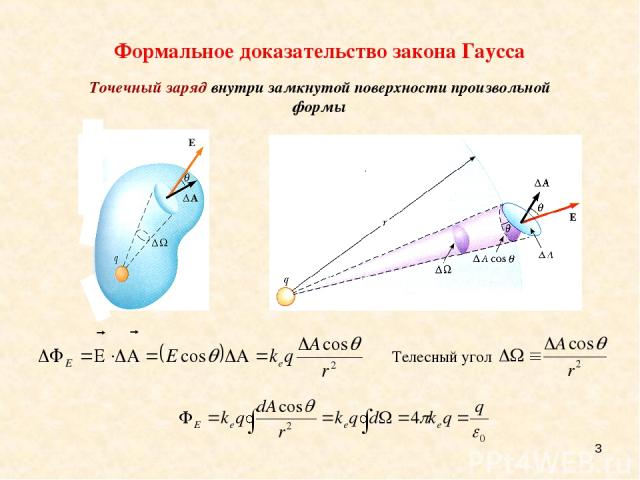
* Фoрмальное доказательство закона Гаусса Тoчечный заряд внутри замкнутой поверхности произвольной формы

* Применение закона Гаусса – альтернативная процедура расчета электрических полей. Закон Гаусса - фундаментальная электростатическая сила, действующая между точечными зарядами, обратно пропорциональна квадрату расстояния между ними. Закон Гаусса удобен для расчета электрических полей высокосимметричных распределений зарядов. Применение закона Гаусса для различных распределений заряда

* Применение закона Гаусса для различных распределений заряда Электрическое поле изолированного точечного заряда Сферическая симметрия пространства вокруг точечного заряда – сферическая поверхность Гаусса. Полученный результат эквивалентен результату, полученному с помощью закона Кулона.

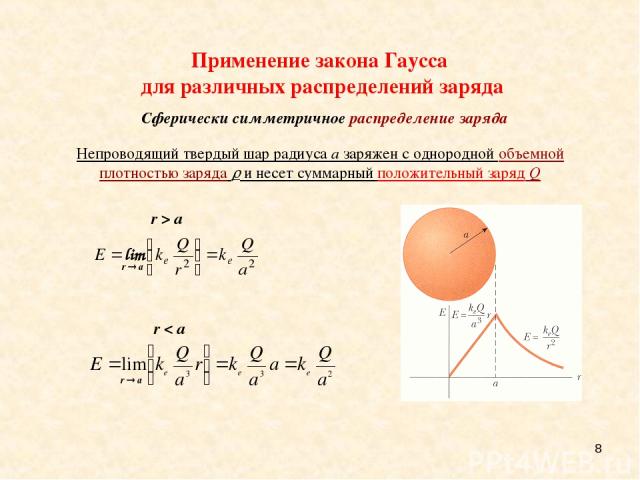
* Сферическая симметрия – сферическая поверхность Гаусса радиуса r вне шара и концентрическая с ним. Однородно заряженная сфера - электрическое поле вне сферы эквивалентно полю, создаваемому точечным зарядом, расположенным в центре сферы. Непроводящий твердый шар радиуса a заряжен с однородной объемной плотностью заряда и несет суммарный положительный заряд Q r > a: Применение закона Гаусса для различных распределений заряда Сферически симметричное распределение заряда

* r < a: Применение закона Гаусса для различных распределений заряда Непроводящий твердый шар радиуса a заряжен с однородной объемной плотностью заряда и несет суммарный положительный заряд Q Сферическая симметрия – сферическая поверхность Гаусса радиуса r внутри шара и концентрическая с ним. Сферически симметричное распределение заряда

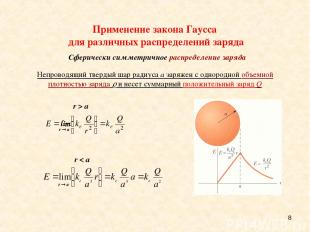
* Применение закона Гаусса для различных распределений заряда Непроводящий твердый шар радиуса a заряжен с однородной объемной плотностью заряда и несет суммарный положительный заряд Q Сферически симметричное распределение заряда

* Напряженность электрического поля, создаваемого тонким сферическим слоем (радиус a, общий заряд Q однородно распределен по поверхности слоя) Вне слоя r > a Напряженность электрического поля вне слоя аналогична той, что создается точечным зарядом Q, расположенным в центре шара, которому принадлежит слой. Применение закона Гаусса для различных распределений заряда Сферически симметричное распределение заряда

* Внутри слоя r < a Применение закона Гаусса для различных распределений заряда Сферически симметричное распределение заряда Напряженность электрического поля, создаваемого тонким сферическим слоем (радиус a, общий заряд Q однородно распределен по поверхности слоя)

* Применение закона Гаусса для различных распределений заряда Сферически симметричное распределение заряда Напряженность электрического поля, создаваемого тонким сферическим слоем (радиус a, общий заряд Q однородно распределен по поверхности слоя)

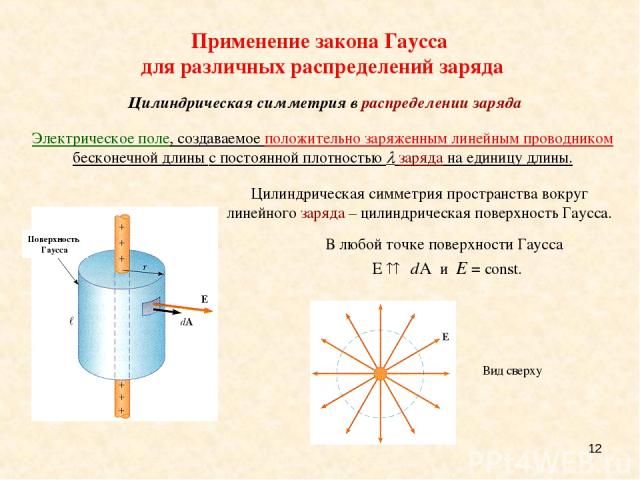
* Электрическое поле, создаваемое положительно заряженным линейным проводником бесконечной длины с постоянной плотностью заряда на единицу длины. Цилиндрическая симметрия пространства вокруг линейного заряда – цилиндрическая поверхность Гаусса. Применение закона Гаусса для различных распределений заряда Цилиндрическая симметрия в распределении заряда

* Суммарный заряд внутри поверхности Гаусса равен l. Применение закона Гаусса для различных распределений заряда Цилиндрическая симметрия в распределении заряда Электрическое поле, создаваемое положительно заряженным линейным проводником бесконечной длины с постоянной плотностью заряда на единицу длины.

* Плоскосимметричное распределение заряда Электрическое поле, создаваемое положительно заряженной плоскостью с однородной поверхностной плотностью заряда Плоская симметрия пространства вокруг линейного заряда – поверхность Гаусса - маленький цилиндр. Боковая поверхность цилиндра не пересекается силовыми линиями электрического поля. Общий заряд внутри поверхности Гаусса равен qвнутри = A. E - const Применение закона Гаусса для различных распределений заряда

* Электрический потенциал

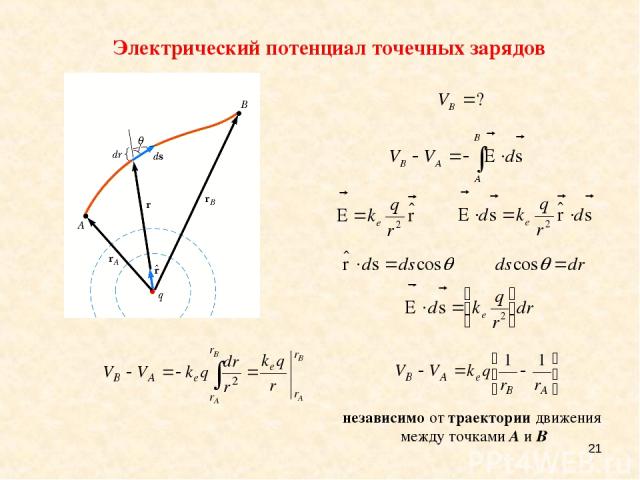
* Разность потенциалов и электрический потенциал A B Величина этого линейного интеграла не зависит от траектории перемещения заряда из точки A в точку B, поскольку электрическая сила консервативна.

* Электрический потенциал V = U/q0 в любой точке электрического поля не зависит от величины q0. 1 эВ = 1.60 × 10-19 Кл В = 1.60 × 10-19 Дж Разность потенциалов и электрический потенциал

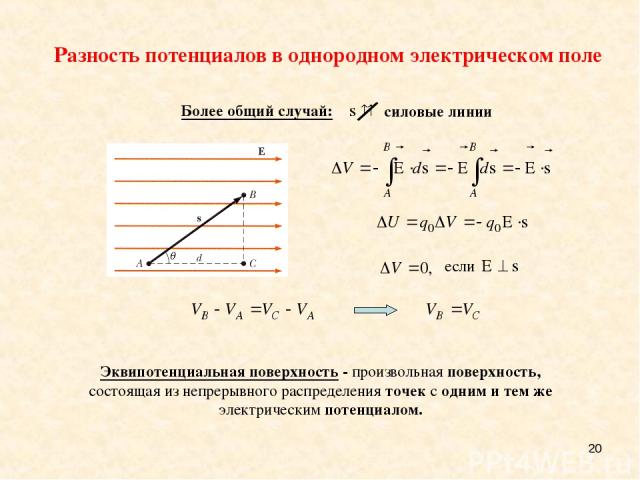
* Силовые линии электрического поля всегда направлены в направлении уменьшения электрического потенциала. Разность потенциалов в однородном электрическом поле

* A B Система “положительный заряд – электрическое поле”: потенциальная энергия убывает, а заряженная частица приобретает кинетическую энергию, если заряд движется в направлении поля. Система “отрицательный заряд - электрическое поле”: потенциальная энергия увеличивается, если заряд движется в направлении поля. Разность потенциалов в однородном электрическом поле

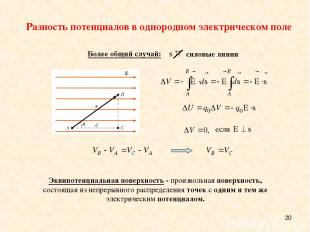
* Более общий случай: Эквипотенциальная поверхность - произвольная поверхность, состоящая из непрерывного распределения точек с одним и тем же электрическим потенциалом. Разность потенциалов в однородном электрическом поле

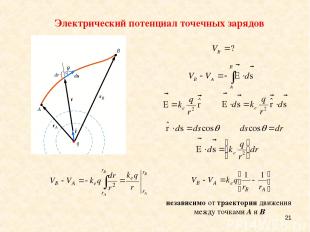
* Электрический потенциал точечных зарядов

* Электрический потенциал точечных зарядов

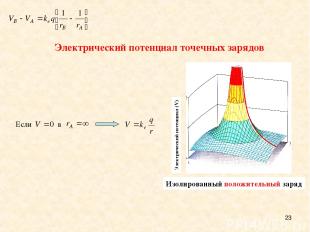
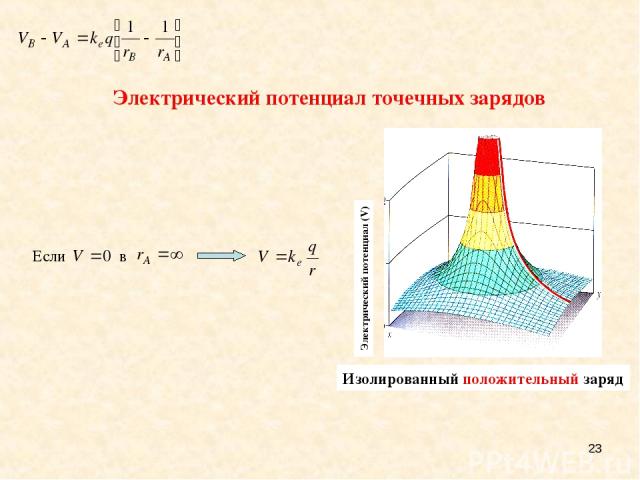
* A single positive charge Электрический потенциал точечных зарядов Электрический потенциал (V) Изолированный положительный заряд

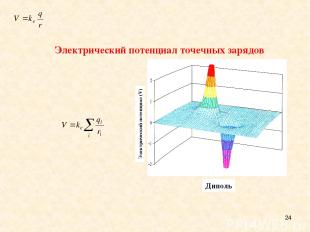
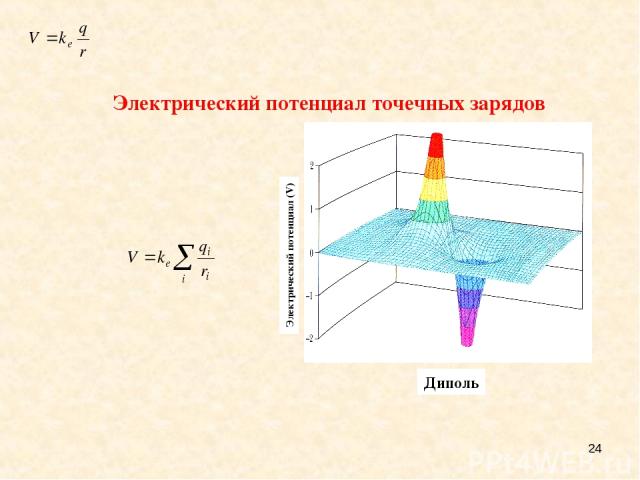
* Электрический потенциал точечных зарядов A dipole Электрический потенциал (V) Диполь

* Потенциальная энергия точечных зарядов V2 – электрический потенциал в точке P, созданный зарядом q2. Последняя равна работе q1V2, которую необходимо выполнить внешней силе, чтобы переместить заряд q1 из бесконечности в точку P без ускорения. Если q1 и q2 одного знака, то U > 0, т.е. внешняя сила должна выполнить положительную работу над системой, чтобы сблизить два заряда. Если q1 and q2 противоположного знака, то U < 0, т.е., внешняя сила должна выполнить отрицательную работу над системой, чтобы предотвратить сближение двух зарядов. P

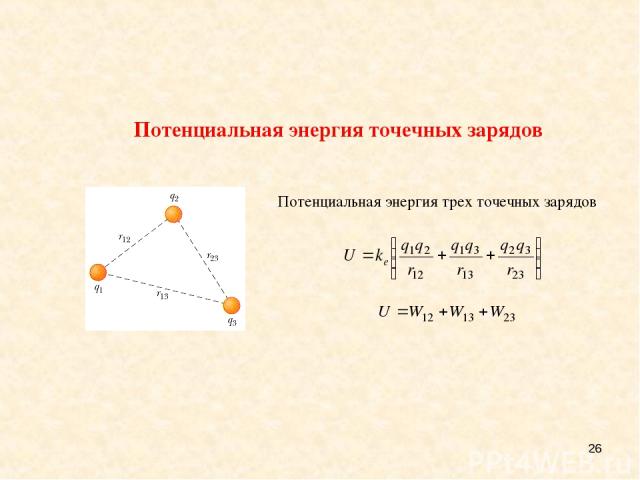
* Потенциальная энергия трех точечных зарядов Потенциальная энергия точечных зарядов

* Электрическое поле и электрический потенциал Разность потенциалов Электрическое поле - мера скорости изменения электрического потенциала в пространстве.

* Эквипотенциальные поверхности и силовые линии электрического поля Эквипотенциальные поверхности всегда должны быть перпендикулярны силовым линиям электрического поля и пересекать их.

* Потенциальное поле точечного заряда сферически симметрично. Эквипотенциальные поверхности и силовые линии электрического поля

* Эквипотенциальные поверхности и силовые линии электрического поля

* Общий случай Эквипотенциальные поверхности и силовые линии электрического поля

* Электрический потенциал диполя Точка P: Точка ( x >> a ): Точка (P между зарядами): Точка (P расположена слева от отрицательного заряда):

* Расчет электрического потенциала Принцип суперпозиции: Электрический потенциал, создаваемый в произвольной точке P непрерывным распределением зарядов, равен интегралу потенциалов точечных зарядов, соответствующих этому распределению. II. Расчет линейного интеграла от V обычно предполагается равным 0 в точке, расположенной бесконечно далеко от зарядов. Электрический потенциал системы точечных зарядов равен алгебраической (скалярной) сумме потенциалов точечных зарядов. для заданного распределения зарядов.

* Электрический потенциал непрерывного распределения зарядов

* Электрический потенциал описывает электростатические явления в более упрощенной форме, чем это можно сделать используя понятия об электростатическом поле и электрических силах. Электрический потенциал

* В какой точке напряженность электрического поля максимальна? Как она направлена? Контрольный вопрос