Презентация на тему: Свойства жидкостей

Свойства жидкостей. Поверхностное натяжение Урок в 10 классе

1. Молекулы вещества в жидком состоянии расположены почти вплотную друг к другу. 2. В отличие от твердых кристаллических тел, в которых молекулы образуют упорядоченные структуры во всем объеме кристалла и могут совершать тепловые колебания около фиксированных центров, молекулы жидкости обладают большей свободой. 3. Каждая молекула жидкости, также как и в твердом теле, «зажата» со всех сторон соседними молекулами и совершает тепловые колебания около некоторого положения равновесия.

4. Однако, время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах , и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. 5. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком (рис. 1).

Рисунок 1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед.

Рис. 2 иллюстрирует отличие газообразного вещества от жидкости на примере воды. Молекула воды H2O состоит из одного атома кислорода и двух атомов водорода, расположенных под углом 104°. Среднее расстояние между молекулами пара в десятки раз превышает среднее расстояние между молекулами воды. В отличие от рис. 1, где молекулы воды изображены в виде шариков, рис. 2 дает представление о структуре молекулы воды. Рисунок 2. Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·10(7) раз.

Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах.

Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Если молекула переместиться с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу.

Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), надо затратить положительную работу внешних сил ΔA внеш, пропорциональную изменению ΔS площади поверхности: ΔA внеш = σΔS.

Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу. В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2).

Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Ep поверхности жидкости пропорциональна ее площади: Ep = Aвнеш = σS.

Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.

Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости. Сечение сферической капли жидкости.

Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела.

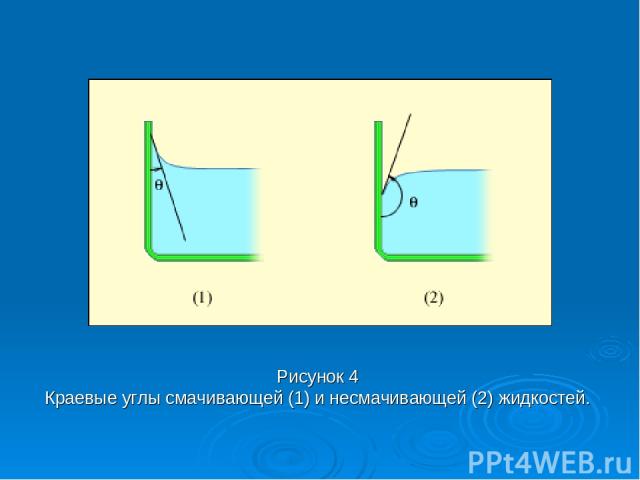
В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 4). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачивании θ = 0, при полном несмачивании θ = 180°.

Рисунок 4 Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.

Капиллярные явления Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.

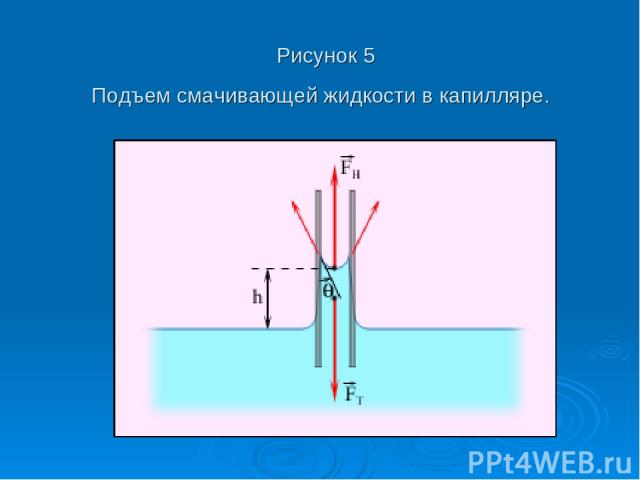
Рисунок 5 Подъем смачивающей жидкости в капилляре.

На рис. 5 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fн сил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.

Отсюда следует:

При полном смачивании θ = 0, cos θ = 1. В этом случае: При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.

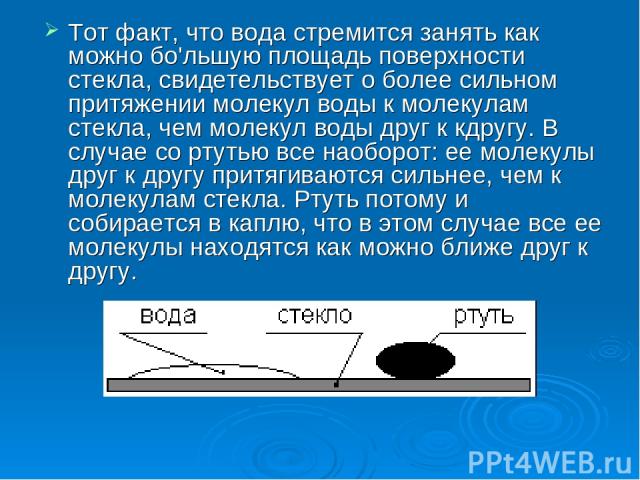
Явление смачивания - несмачивания. Мы привыкли, что чернила хорошо впитываются в бумагу, нас не удивляет, что вода хорошо пропитывает ткань. Так происходит потому, что эти жидкости хорошо смачивают большинство предметов. Но вода, к примеру, не смачивает жирные поверхности. Ртуть же, в противоположность воде, совсем не смачивает стекло. Она собирается на его поверхности в виде капелек, в то время когда вода растекается тонким слоем. В чем причина явления смачивания?

Тот факт, что вода стремится занять как можно бо'льшую площадь поверхности стекла, свидетельствует о более сильном притяжении молекул воды к молекулам стекла, чем молекул воды друг к кдругу. В случае со ртутью все наоборот: ее молекулы друг к другу притягиваются сильнее, чем к молекулам стекла. Ртуть потому и собирается в каплю, что в этом случае все ее молекулы находятся как можно ближе друг к другу.

Итак, явление смачивания-несмачивания объясняется различным взаимодействием молекул тела и жидкости. Если молекулы жидкости притягиваются к телу сильнее, чем друг к другу, то такая жидкость смачивает тело. Если же молекулы жидкости притягиваются друг к другу сильнее, чем к телу, то жидкость не будет смачивать данное тело.

Явление смачивания-несмачивания часто встречается в природе и быту. Например, водоплавающие птицы смазывают перья жиром, выделяющимся из специальных желез (внутренних органов птицы). Вода не смачивает жир и, поэтому, перья остаются сухими даже при нырянии (пословица "как с гуся вода"). Благодаря явлению смачивания мы можем вытираться полотенцами, мыть посуду, стирать белье. Благодаря явлению несмачивания мы можем ходить под зонтами и в плащах, не промокающих под дождем.

С явлением смачивания-несмачивания очень тесно связано явление капиллярности. Познакомимся с ним на опыте. Если стеклянную трубку опустить в чашу с водой, то внутри трубки вода поднимется на некоторую высоту (левый рисунок). Ртуть, напротив, опустится ниже уровня в чаше (правый рисунок). Это явление подъема или опускания уровня жидкости в тонких трубках по сравнению с уровнем жидкости в широком сосуде называется явлением капиллярности, а трубки для наблюдения этого явления – капиллярами (греч. "капиллус" – волос).

Из рассмотренных примеров нетрудно заметить, что жидкости, смачивающие материал, из которого сделан капилляр, будут в нем подниматься (вода и стекло). И наоборот: жидкости, не смачивающие капилляр, будут в нем опускаться (стекло и ртуть). Кроме того, высота подъема (опускания) жидкости зависит от толщины трубки: чем тоньше капилляр, тем больше высота поднятия (опускания) жидкости.

Объясним явление капиллярности. Рассмотрим следующий опыт. В сосуд с водой опустим две стеклянные пластинки. Поскольку стекло смачивается водой, то вблизи поверхности пластинок водная поверхность в сосуде искривится. Вода как бы "прильнет" к стеклам, пытаясь "всползти" по ним вверх (рис. 1). Вы видите, что искривление водной поверхности происходит как на внешней, так и на внутренней стороне пластинок. Приближая стекла друг к другу (см. рисунки 2, 3), мы сблизим искривившиеся водные поверхности, и нижние их части сомкнутся уже выше уровня воды в сосуде (см. рисунки 3, 4). Получается, что мы сконструировали "действующую модель" капилляра.