Презентация на тему: Реактор ИТЭР

Курс лекций: Физико-технические основы токамака-реактора ИТЭР Владимир Юрьевич Сергеев проф., д.ф.м.н., кафедра физики плазмы физико-технический факультет СПбГПУ 900igr.net

* Содержание лекции № 8-10 «Динамика и перенос в пьедестале» 8.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 8.2. Структура и характеристики пьедестала 8.3. L-H переходы 9.1. Теория и моделирование переноса в пьедестале 9.2. Моделирование структуры пьедестала 9.3. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 10.1. Альтернативы режиму «Type I ELMy H-mode» 10.2. Устойчивость пьедестала 10.3. Возможные сценарии управления пьедесталом

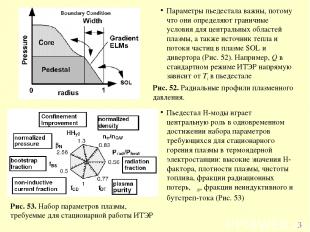
* Параметры пьедестала важны, потому что они определяют граничные условия для центральных областей плазмы, а также источник тепла и потоки частиц в плазме SOL и дивертора (Рис. 52). Например, Q в стандартном режиме ИТЭР напрямую зависит от Ti в пьедестале Рис. 52. Радиальные профили плазменного давления. Рис. 53. Набор параметров плазмы, требуемые для стационарной работы ИТЭР Пьедестал H-моды играет центральную роль в одновременном достижении набора параметров требующихся для стационарного горения плазмы в термоядерной электростанции: высокие значения H-фактора, плотности плазмы, чистоты топлива, фракции радиационных потерь, βN, фракции неиндуктивного и бутстреп-тока (Рис. 53)

* Поясним сказанное выше. Благодаря «жесткости» профиля температуры, удержание энергии и Q зависят от температуры пьедестала, которая уменьшается с ростом плотности пьедестала, потому что давление пьедестала примерно постоянно из-за ELMs. Поэтому, чтобы достичь хорошего удержания энергии при большей плотности, нужно как-то повышать давление. Для МГД устойчивости при больших βN нужно также увеличивать давление пьедестала, чтобы достичь широкого профиля давления в центре, так как умеренный градиент давления в центральных областях стабилизирует глобальные идеальные моды с малыми n и NTM. Для поддержания профиля тока с оптимальной для удержания и устойчивости формой, распределения граничного бустреп-тока также должно быть оптимальным. Температура, плотность пьедестала и ELMs определяют экранирование и накачку примесей, таким образом, играя ключевую роль в управлении частицами (чистоте) плазмы. С другой стороны, надо следить за минимальными тепловыми нагрузками ELM на диверторные пластины, которые растут в срывах Type I ELM с ростом давления пьедестала. Отсюда следует, что в зависимости от задач, давление в пьедестале надо оптимизовать.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* Одна из основных физических проблем, сформулированных в IPB (1999), это трудность поддержания Н-моды при больших плотностях плазмы, обеспечиваемых газовым напуском. Type I ELMy H-mode confinement database показывает, что τE~ nе0.41 при умеренных плотностях и насыщается, или даже снижается при приближении к операционному пределу (Гринвальда). Напомним: Фактор улучшенного удержания: HH98(y,2) = texp/ tH98,y2 ; texp = W/P ; где W - энергосодержание плазмы, а P – вкладываемая мощность Известный скейлинг для времени удержания: tH98,y2 ~ ne0.41 Подставив, получается HH98(y,2) = W/ (P × ne0.41)

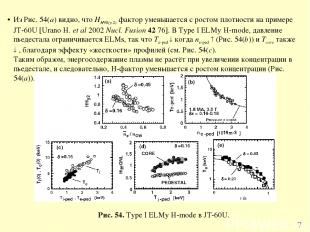
* Из Рис. 54(a) видно, что HH98(y,2) фактор уменьшается с ростом плотности на примере JT-60U [Urano H. et al 2002 Nucl. Fusion 42 76]. В Type I ELMy H-mode, давление пьедестала ограничивается ELMs, так что Tе-рed когда nе-рed (Рис. 54(b)) и Tcore также , благодаря эффекту «жесткости» профилей (см. Рис. 54(c). Таким образом, энергосодержание плазмы не растёт при увеличении концентрации в пьедестале, и следовательно, H-фактор уменьшается с ростом концентрации (Рис. 54(а)). Рис. 54. Type I ELMy H-mode в JT-60U.

* Таким образом, основные факторы определяющие деградацию удержания при больших ne – это ограничение давления пьедестала ELMs и жесткость профилей Несколько методов было обнаружено позволяющие сохранить H-моду с хорошим удержанием при плотностях близких, или даже выше предела Гринвальда: 1) увеличение треугольности [Saibene G. et al 1999 Nucl. Fusion 39 1133], 2) глубокое проникновение пеллетов, сильный газонапуск в экваториальной плоскости комбинированный с интенсивной откачкой дивертора [Mahdavi M.A. et al 2002 Nucl. Fusion 42 52], 3) небольшой постоянный газовый напуск ведущий к пикированию плотности [Valovic M. et al 2002 Plasma Phys. Control. Fusion 44 1911] 4) контролируемая инжекция примеси [Ongena J. et al 2004 Nucl. Fusion 44 124]. Рассмотрим первые 2 метода 4.1.1. Эффекты влияния формы плазмы на глобальное удержание и удержание в пьедестале При большой треугольности, δ, хороший фактор удержания может быть сохранен при большой плотности потому, что улучшается устойчивость по отношению к ELMs [Snyder P.B. and Wilson H.R. 2003 Plasma Phys. Control. Fusion 45 1671]. При δ, граничное давление выше, Tе-рed и Tcore при заданной плотности пьедестала (Рис. 54(е), и, соответственно, HH98(y,2) (Рис. 54(а)). Рис. 55 иллюстрирует поведение на JET и ASDEX Upgrade при различных фиксированных значениях δ. HH98(y,2) с при фиксированной δ и с δ при фиксированном . При высоких (δ = 0.35–0.45), HH98(y,2) достигает 1 при ______≈ 1.1 на обоих установках.

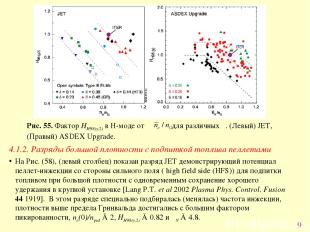
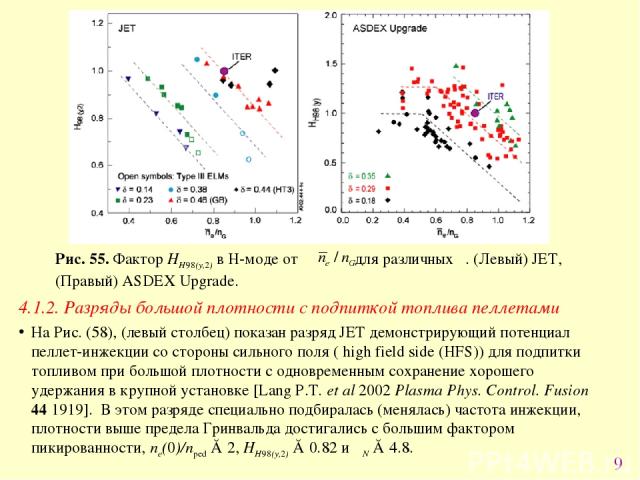
* 4.1.2. Разряды большой плотности с подпиткой топлива пеллетами На Рис. (58), (левый столбец) показан разряд JET демонстрирующий потенциал пеллет-инжекции со стороны сильного поля ( high field side (HFS)) для подпитки топливом при большой плотности с одновременным сохранение хорошего удержания в крупной установке [Lang P.T. et al 2002 Plasma Phys. Control. Fusion 44 1919]. В этом разряде специально подбиралась (менялась) частота инжекции, плотности выше предела Гринвальда достигались с большим фактором пикированности, ne(0)/nped ≈ 2, HH98(y,2) ≈ 0.82 и βN ≈ 4.8.

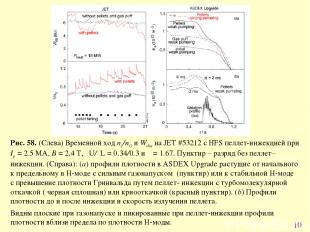
* Рис. 58. (Слева) Временной ход ne/nG и Wdia на JET #53212 с HFS пеллет-инжекцией при Ip = 2.5 MA, B = 2.4 T, δU/δL = 0.34/0.3 и κ = 1.67. Пунктир – разряд без пеллет–инжекции. (Справа): (a) профили плотности в ASDEX Upgrade растущие от начального к предельному в H-моде с сильным газонапуском (пунктир) или к стабильной H-моде с превышение плотности Гринвальда путем пеллет- инжекции с турбомолекулярной откачкой ( черная сплошная) или криооткачкой (красный пунктир). (b) Профили плотности до и после инжекции и скорость излучения пеллета. Видны плоские при газонапуске и пикированные при пеллет-инжекции профили плотности вблизи предела по плотности H-моды.

* 4.1.3. Процессы, ограничивающие плотность Есть несколько пределов по плотности в токамаках [Greenwald M. 2002 Plasma Phys. Control. Fusion 44 R27]. Два из них, H-mode density limit связанный с обратным переходом из H- в L-моду и собственно сам предел по плотности в L-моде приводящий к срыву, наиболее важны для реактора. Параметр определяющий предел по плотности в L-моде – плотность Гринвальда, nG=Ip/pa2 ≡ 1.59gBt/(q95R) (nG [1020 м -3], Ip [МА], Bt [T], a,R[м]), (12), где g = q95/qcyl – фактор формы плазмы с цилиндрическим qcyl = 5a2Bt/(RIp). Обычно, при работе в the Type I ELMy H-mode с газонапуском, увеличение плотности выше некого значения ведет к переходу от Type I к Type III ELMs сопровождающимся снижение на 15–40% запасенной в плазме тепловой энергии [Sartori R. et al 2002 Plasma Phys. Control. Fusion 44 1801]. Дальнейшее увеличение скорости ввода газа ведет к переходу в L-моду, с полным «отрывом» (detachment) дивертора и/или формированием MARFE в диверторной X-точке [ITER Physics Basis Editors et al 1999 Nucl. Fusion 39 2137]. При еще больших скоростях ввода топлива, случается срыв разряда по пределу плотности в L-моде. Для Н-моды наиболее известная модель Боррасса (Borrass) в которой разобрана модель SOL и определяется максимально допустимая там плотность ([1020 м-3, МВт/м2, T, м]), (13), где nBLS = nped ≈ , q = (Pheat − Ptotrad)/Ssep, где Ssep – площадь сепаратрисы

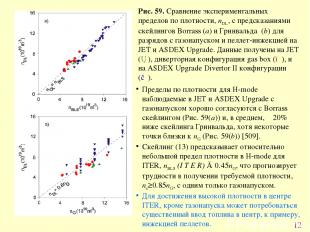
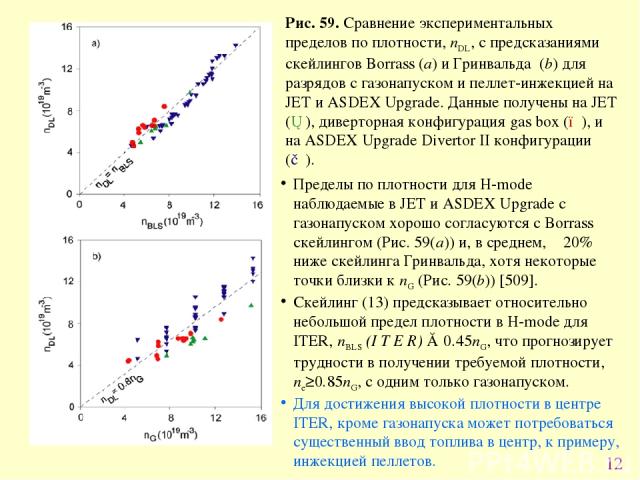
* Рис. 59. Сравнение экспериментальных пределов по плотности, nDL, с предсказаниями скейлингов Borrass (a) и Гринвальда (b) для разрядов с газонапуском и пеллет-инжекцией на JET и ASDEX Upgrade. Данные получены на JET (▲), диверторная конфигурация gas box (●), и на ASDEX Upgrade Divertor II конфигурации (▼). Пределы по плотности для H-mode наблюдаемые в JET и ASDEX Upgrade с газонапуском хорошо согласуются с Borrass скейлингом (Рис. 59(a)) и, в среднем, ∼20% ниже скейлинга Гринвальда, хотя некоторые точки близки к nG (Рис. 59(b)) [509]. Скейлинг (13) предсказывает относительно небольшой предел плотности в H-mode для ITER, nBLS (I T E R) ≈ 0.45nG, что прогнозирует трудности в получении требуемой плотности, ne≥0.85nG, с одним только газонапуском. Для достижения высокой плотности в центре ITER, кроме газонапуска может потребоваться существенный ввод топлива в центр, к примеру, инжекцией пеллетов.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* 4.2.1. Важность характеристик пьедестала в H-mode ITER будет функционировать вблизи предела по плотности, чтобы достичь максимального термоядерного выхода, Pfus~n2 , а так же для преодоления значения мощности, необходимого для перехода в H-mode, Pfus/PLH ~ nx , где 1 < x < 1.4. Кроме того, как отмечалось ранее, наблюдается улучшение удержания с ростом температуры при постоянной плотности. Таким образом, для максимизации эффективности требуется повышать давление в пьедестале. К сожалению, с ростом давления увеличиваются потери энергии за счёт ELM и вмести с ними нагрузка на дивертор. Приемлемый уровень потерь грубо оценивается 5–10% энергосодержания в пьедестале Wped = (3/2)×pped×V . В современных токамаках так и происходит, для ITER может потребоваться подавление Type I ELM или нахождение иного режима функционирования с высоким давлением. 4.2.2. Требования и прогнозирование для ширины транспортного барьера в H-mode. Согласно модели peeling–ballooning mode [Snyder P.B. et al 2004 Nucl. Fusion 44 320] существует пороговое значение градиента давления в пьедестале при котором начинается развитие ELM. Для достижения необходимой для зажигания температуры пьедестала 2÷4 кэВ при ограниченной величине градиента давления требуется ширина 1 %

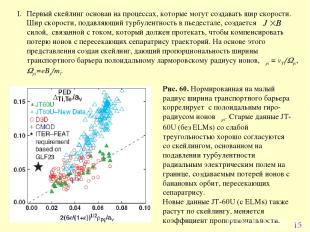
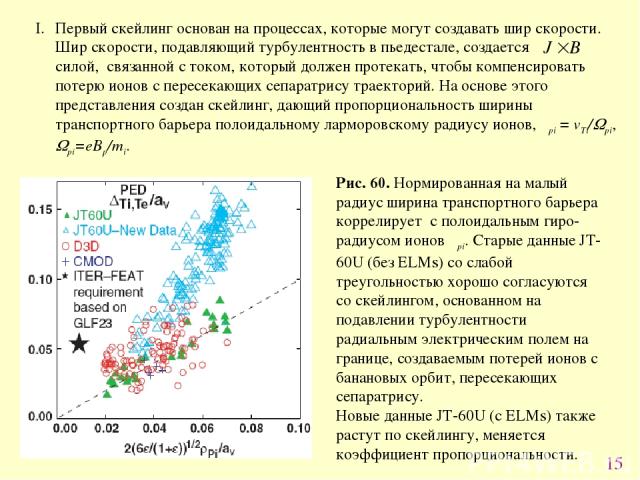
* Рис. 60. Нормированная на малый радиус ширина транспортного барьера коррелирует с полоидальным гиро-радиусом ионов ρpi. Старые данные JT-60U (без ELMs) со слабой треугольностью хорошо согласуются со скейлингом, основанном на подавлении турбулентности радиальным электрическим полем на границе, создаваемым потерей ионов с банановых орбит, пересекающих сепаратрису. Новые данные JT-60U (с ELMs) также растут по скейлингу, меняется коэффициент пропорциональности. Первый скейлинг основан на процессах, которые могут создавать шир скорости. Шир скорости, подавляющий турбулентность в пьедестале, создается силой, связанной с током, который должен протекать, чтобы компенсировать потерю ионов с пересекающих сепаратрису траекторий. На основе этого представления создан скейлинг, дающий пропорциональность ширины транспортного барьера полоидальному ларморовскому радиусу ионов, ρpi = vTi/Wpi, Wpi=еBp/mi.

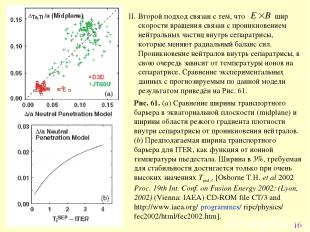
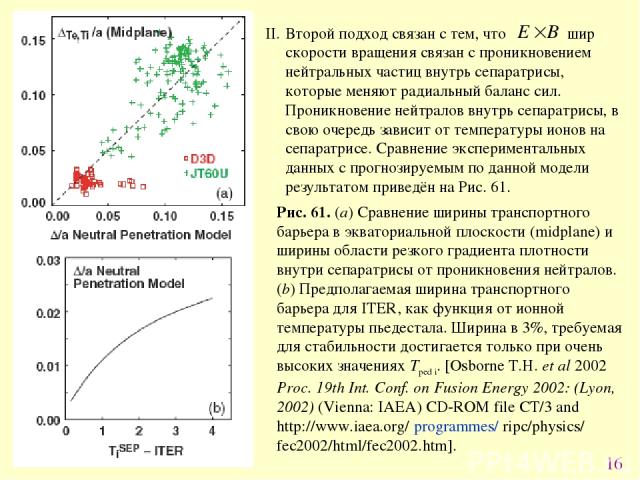
* Рис. 61. (a) Сравнение ширины транспортного барьера в экваториальной плоскости (midplane) и ширины области резкого градиента плотности внутри сепаратрисы от проникновения нейтралов. (b) Предполагаемая ширина транспортного барьера для ITER, как функция от ионной температуры пьедестала. Ширина в 3%, требуемая для стабильности достигается только при очень высоких значениях Tped i. [Osborne T.H. et al 2002 Proc. 19th Int. Conf. on Fusion Energy 2002: (Lyon, 2002) (Vienna: IAEA) CD-ROM file CT/3 and http://www.iaea.org/ programmes/ ripc/physics/ fec2002/html/fec2002.htm].

* цчAnother approach to determining the barrier width is based on the idea that the inner edge of the barrier is defined by the point at which the velocity shear is sufficient to quench the turbulence [523]. В итоге, на основе этих подходов был создан несколько скейлингов, учитывающих основные обнаруженные закономерности. the required pedestal width for ITER is met. 2÷4 кэВ при ограниченной величине градиента давления требуется ширина 1 %

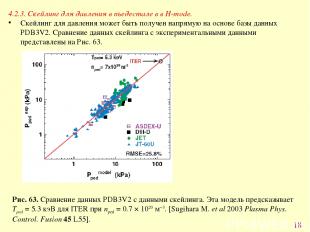
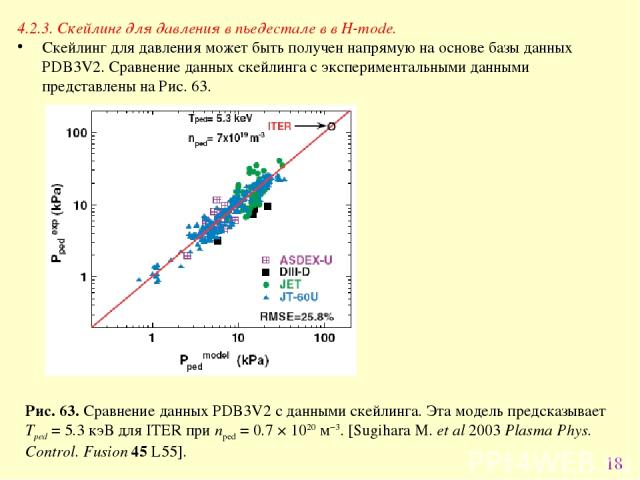
* 4.2.3. Скейлинг для давления в пьедестале в в H-mode. Скейлинг для давления может быть получен напрямую на основе базы данных PDB3V2. Сравнение данных скейлинга с экспериментальными данными представлены на Рис. 63. Рис. 63. Сравнение данных PDB3V2 с данными скейлинга. Эта модель предсказывает Tped = 5.3 кэВ для ITER при nped = 0.7 × 1020 м−3. [Sugihara M. et al 2003 Plasma Phys. Control. Fusion 45 L55].

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* В этом разделе приводится ряд экспериментально установленных фактов по переходу разряда из L-mode в H-mode (L-H переход). На основе обширной базы данных создан скейлинг для пороговой мощности PLH = 0.042×n200.73×Bt0.74 ×S0.98 , где S – площадь сепаратрисы (26) PLH = 0.072×n200.7×Bt0.7 ×S0.9×(Zeff/2)0.7×F(A)γ (27) Видно, что процессе L-H перехода основные параметры играющие роль - плотность плазмы, магнитное поле и размеры плазмы. Последние исследования позволили учесть роль аспектного отношения и эффективного заряда плазмы при оценке пороговой мощности. Здесь F(A) =0.1×А/f (A), f (A)=1-[2/(1+А)]0.5, γ=0.5. Используя это выражение с Zeff=2, пороговая мощность для ITER оценивается в 40-50 МВт, что реализуемо.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* Среди всех теорий (см. обзор [Connor J.W. and Wilson H.R. 2000 Plasma Phys. Control.Fusion 42 R1]) экспериментальное подтверждение получили те, в основе которых лежит гипотеза о подавлении турбулентности электрическим полем с широм. Тем не менее, механизм генерации этого поля и механизм запуска остаются неясными. В разных условиях могут быть разные механизмы и не существует единой теории описывающей весь спектр наблюдаемых явлений. В подавлении турбулентности кроме основных потоков могут участвовать ещё и зональные потоки, которые генерируются турбулентностью. Они, как бы, забирают часть энергии у турбулентности, распределяя её в осесимметричных модах, которые не оказывают влияние на радиальный перенос. Учёт зональных потоков приводит к снижению порога L-H перехода.

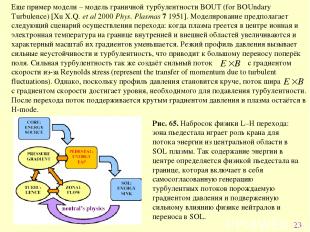
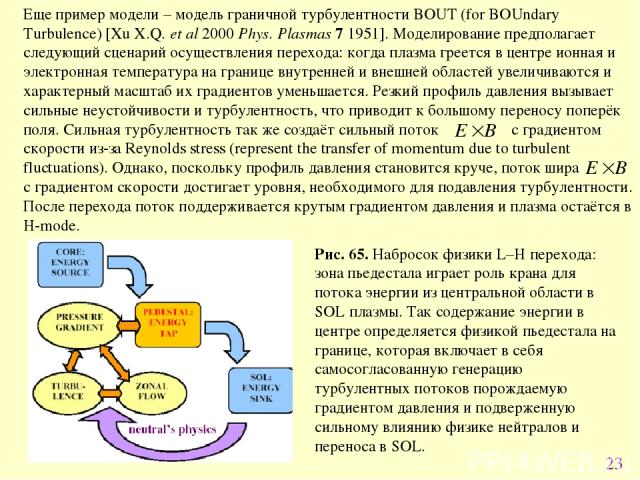
* Рис. 65. Набросок физики L–H перехода: зона пьедестала играет роль крана для потока энергии из центральной области в SOL плазмы. Так содержание энергии в центре определяется физикой пьедестала на границе, которая включает в себя самосогласованную генерацию турбулентных потоков порождаемую градиентом давления и подверженную сильному влиянию физике нейтралов и переноса в SOL.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

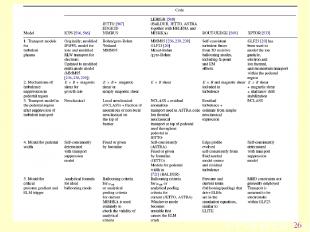
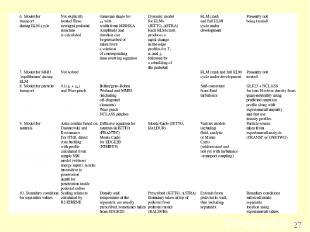
* Основная цель моделирования структуры пьедестала понять и предсказать изменение во времени его ширины и высоты для температуры и концентрации плазмы. Так же она может пониматься как граничные условия для внутренней и внешней областей плазмы. Но на параметры пьедестала оказывают влияние как внешние так и внутренние области плазмы, так что моделирование пьедестала требует интеграции с моделированием центра и внешней области. Пока при моделировании на сепаратрисе ставятся граничные условия по результатам моделирования SOL/divertor кодов. Одной из главных сложностей моделирования является наличие процессов с существенно разными временными масштабами от времени переноса до быстрых МГД процессов. Большинство кодов основано на транспортном коде с дополнительным описанием турбулентного переноса и переноса за счёт МГД процессов. МГД процессы могут моделироваться, а могут оцениваться градиент давления и сравниваться с критическим значением, определяемым по простой аналитической формуле. Могут меняться закладываемые в код особенности механизма подавления турбулентности и влияния нейтралов. Основные параметры различных моделей сведены в Таблице 2.

*

*

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

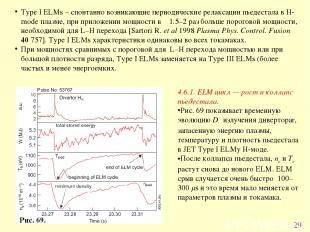
* Type I ELMs – спонтанно возникающие периодические релаксации пьедестала в H-mode плазме, при приложении мощности в ∼1.5–2 раз больше пороговой мощности, необходимой для L–H перехода [Sartori R. et al 1998 Plasma Phys. Control. Fusion 40 757]. Type I ELMs характеристики одинаковы во всех токамаках. При мощностях сравнимых с пороговой для L–H перехода мощностью или при большой плотности разряда, Type I ELMs заменяется на Type III ELMs (более частых и менее энергоемких. 4.6.1. ELM цикл — рост и коллапс пьедестала. Рис. 69 показывает временную эволюцию Dα излучения дивертораr, запасенную энергию плазмы, температуру и плотность пьедестала в JET Type I ELMy H-моде. После коллапса пьедестала, ne и Te растут снова до нового ELM. ELM срыв случается очень быстро 100–300 μs и это время мало меняется от параметров плазмы и токамака. Рис. 69.

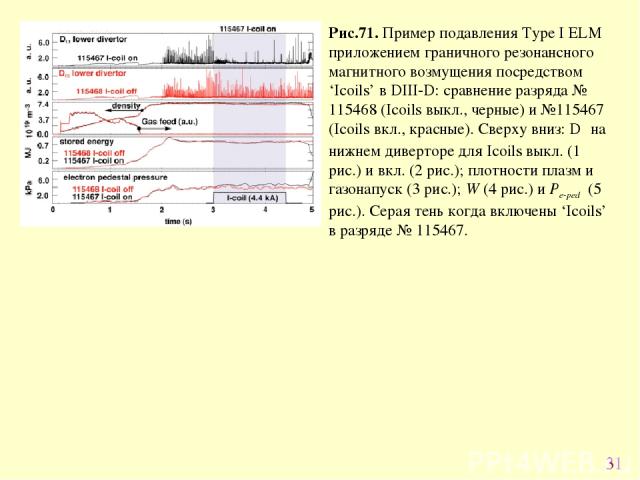
* После срыва, восстановление верха пьедестала более долгое, сопровождающееся перестройкой профилей в пьедестале. ELM срыв вызывает уширение профилей, которые затем пикируются до наступления следующего ELM. ELM срыв сначала происходит со стороны слабого магнитного поля токамака, затем возмущение плотности распространяется на внутреннею сторону приблизительно со скоростью ионного звука, что согласуется с МГД интерпретацией ELM событий как неустойчивости баллонного типа. Выяснено, что потери энергии в ELM происходят в основном за счет конвективного переноса (filaments or blobs). 4.6.2. Техники смягчения (mitigation ) Type I ELM. Время жизни диверторных пластин в ITER за счет эрозии и сублимации во время Type I ELMs значительно снижается. Поэтому развиваются техники сохранения свойств общего переноса плазмы и уменьшения загрузки ELM-мами диверторных элементов. Внешние возмущения – управление пограничным током, пограничным магнитным полем (Рис. 71) и индицирование ELM небольшими пеллетами (Будет обсуждено в последующих лекциях) – придумано на данный момент и обсуждены здесь, а в следующем параграфе 4.7. обсуждены режимы плазмы без Type I ELMs. Важно эту работу распространить на токамаки с широким изменением параметров плазмы, а также продемонстрировать совместимость этих техник с MHD устойчивостью плазмы.

* Рис.71. Пример подавления Type I ELM приложением граничного резонансного магнитного возмущения посредством ‘Icoils’ в DIII-D: сравнение разряда № 115468 (Icoils выкл., черные) и №115467 (Icoils вкл., красные). Сверху вниз: Dα на нижнем диверторе для Icoils выкл. (1 рис.) и вкл. (2 рис.); плотности плазм и газонапуск (3 рис.); W (4 рис.) и Pe-ped (5 рис.). Серая тень когда включены ‘Icoils’ в разряде № 115467.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* 4.7. Альтернативы режиму Type I ELMy H-mode H-моды with Type I ELMs наиболее часто реализуемые и относительно хорошо изученные режимы улучшенного удержания в современных токамаках. Именно он выбран как базовый сценарий для ИТЭР Они, однако, сокращают время жизни диверторных пластин и могут сорвать или прекратить ITB через МГД процессы в центре, связанные с модификацией периферийных профилей [Becoulet M. et al 2003 Plasma Phys. Control. Fusion 45 A93, Polevoi A.R. et al 2003 Nucl. Fusion 43 1072, Turnbull A.D. et al 2003 Plasma Phys. Control. Fusion 45 1845]. Было понято, что нужен механизм для увеличения переноса частиц на границе плазмы с H-модой, иначе частицы и примеси имеют тенденцию к аккумулированию. Чтобы исключить эти потенциальные опасности изучают новые режимы, в которых удержание хорошее, примесь не аккумулируется и при этом нет совсем или есть маленькие ELMs или непрерывные флуктуации на периферии. 4.7.1. Type III ELMs. Type III ELMy H-modes по сравнению с Type I ELMy режимом, имеют выше ELM частоту, меньше потерь энергии на 1 ELM, WELM, но зато сниженное 10–30% время удержание энергии. В отличии от Type I ELMs, Type III ELMs часто наблюдаются в плазмах с ITB, что делает их, в принципе, интересными для будущих приложений

* 4.7.2. Enhanced D-alpha and similar regimes. ‘Enhanced Dα’ (EDA) H-mode режим впервые увиден на Alcator C-Mod в 1996. Глобальное удержание как и в Type I ELMy режиме, HITER89P значениями до 2, в то время как плотность и излучающаяся мощность стационарны по сравнению с обычно свободной от ELM H-модой. Они получаются при q95 > 3.5 и δ > 0.35 и отличаются ELM-free по столкновительности и градиенту давления в периферийной области. 4.7.3. ‘Quiescent’ H-mode. Спокойная ‘quiescent H-mode’ (QH режим) впервые обнаружен на DIII-D в 1999 и потом воспроизведен на ASDEX Upgrade. Подобно EDA режиму, он демонстрирует хорошее удержание, похожее на тот что в Type I ELMy режиме, и имеет достаточный перенос частиц, чтобы остановить аккумуляцию частиц и примесей. 4.7.4. Type II ELMs. Первый переход от Type I ELMs к малым ELMs с хорошим удержанием плазмы был обнаружен DIII-D в 1990 в single-null разряде с повышением вытянутости и треугольности плазмы и малым током (κ = 1.8, δ ∼ 0.5, q95 ∼ 7), и объяснялся изменением МГД устойчивости на границе плазмы. Особенность режима – совместное сосуществование большого давления пьедестала и иррегулярных с высокой частотой очень маленьких ELMs. 4.7.5. ‘Grassy’ ELMs. Небольшие ELMs с хорошим удержанием плазмы были достигнуты на JT-60U с высокой треугольностью, βp и слабым обратным широм (т.е. в плазмах имеющих как ITB так и ETB).

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* 4.8.1. МГД неустойчивости в пьедестале Есть 2 идеальные МГД неустойчивости связанные с пьедесталом. Балонные моды с большим тороидальным числом моды, n, могут быть неустойчиво если градиент давления превышает определенное критическое значение. Однако, достаточным управлением формой шнура и в присутствии достаточной плотности тока, эти баллонные моды могут стабилизироваться, обеспечивая доступ к более высоким значения градиента давления, к так называемой второй зоне стабильности. Дестабилизирующий эффект градиента давления возникает вследствие того факта, что мода локализована на внешнем обводе тора с неблагоприятной кривизной магнитного поля. Вторая идеальная МГД неустойчивость – пиллинг-мода (the peeling mode), которая как думают есть локализованная на границе кинк-мода [Manickam J. 1992 Phys. Fluids B 4 1901]. Источником неустойчивости является плотность тока (или ее градиент) в области пьедестала. Увеличивая треугольность и вытянутость, можно регулировать плотность тока для стабилизации моды. Когда оба дестабилизирующих источника для 2 МГД неустойчивостей имеются в наличии, обычно при промежуточных значениях n ∼ 6–12, моды известны как связанные пиллинг-баллонные моды the (coupled) peeling–ballooning modes [Snyder P.B. et al 2002 Phys. Plasmas 9 2037]. Развиты несколько кодов для расчета МГД устойчивости в пьедестале. Пример приведен на Рис. 81.

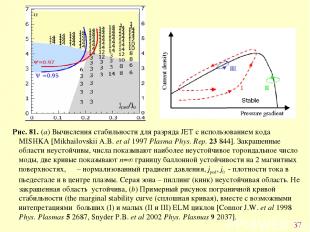
* Рис. 81. (a) Вычисления стабильности для разряда JET с использованием кода MISHKA [Mikhailovskii A.B. et al 1997 Plasma Phys. Rep. 23 844]. Закрашенные области неустойчивы, числа показывают наиболее неустойчивое тороидальное число моды, две кривые показывают n=∞ границу баллонной устойчивости на 2 магнитных поверхностях, α – нормализованный градиент давления, jped, j0 - плотности тока в пьедестале и в центре плазмы. Серая зона – пиллинг (кинк) неустойчивая область. Не закрашенная область устойчива, (b) Примерный рисунок пограничной кривой стабильности (the marginal stability curve (сплошная кривая), вместе с возможными интепретациями больших (I) и малых (II и III) ELM циклов [Connor J.W. et al 1998 Phys. Plasmas 5 2687, Snyder P.B. et al 2002 Phys. Plasmas 9 2037].

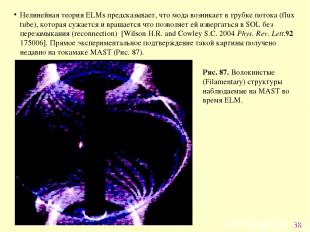
* Нелинейная теория ELMs предсказывает, что мода возникает в трубке потока (flux tube), которая сужается и вращается что позволяет ей извергаться в SOL без перезамыкания (reconnection) [Wilson H.R. and Cowley S.C. 2004 Phys. Rev. Lett.92 175006]. Прямое экспериментальное подтверждение такой картины получено недавно на токамаке MAST (Рис. 87). Рис. 87. Волокнистые (Filamentary) структуры наблюдаемые на MAST во время ELM.

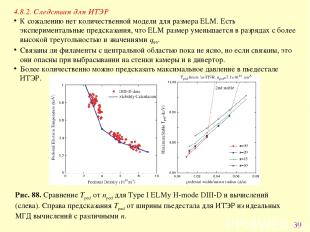
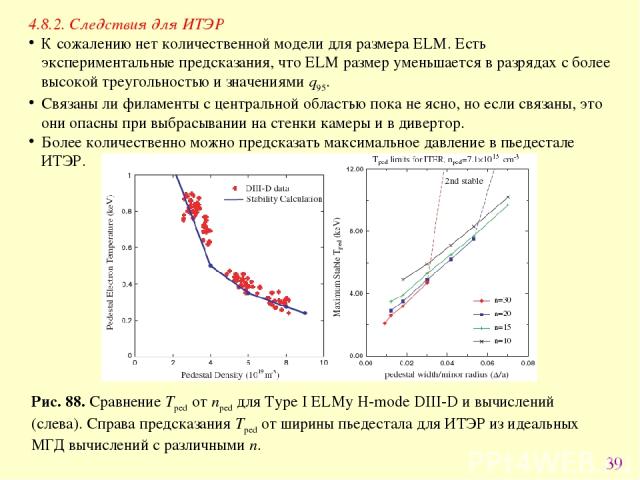
* 4.8.2. Следствия для ИТЭР К сожалению нет количественной модели для размера ELM. Есть экспериментальные предсказания, что ELM размер уменьшается в разрядах с более высокой треугольностью и значениями q95. Связаны ли филаменты с центральной областью пока не ясно, но если связаны, это они опасны при выбрасывании на стенки камеры и в дивертор. Более количественно можно предсказать максимальное давление в пьедестале ИТЭР. Рис. 88. Сравнение Tped от nped для Type I ELMy H-mode DIII-D и вычислений (слева). Справа предсказания Tped от ширины пьедестала для ИТЭР из идеальных МГД вычислений с различными n.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* При управлении пьедесталом (‘pedestal control’), т.е. управлении структурой/профилями параметров пьедестала и активностью ELM, возможные подходы основываются на модификации переноса, распределения нейтралов и МГД устойчивости 4.9.1. Управление высотой и структурой пьедестала С целью максимизировать параметр QDT, согласно современным знаниям, первым шагом надо добиться равновесия с большими значениями вытянутости и треугольности. Мощности для нагрева и поддержания тока нужно прикладывать к центральным областям (не к области пьедестала) также для максимизации QDT. Что касается ввода топлива, пеллет-инжекция кажется благоприятным методом для хорошего удержания при большой плотности, так как снижает число нейтралов окружающих плазму и минимизирует рециркуляцию топлива. Небольшой газонапуск в диверторной области может потребоваться для поддержания условия «отрыва» этой зоны от центра (detached condition). Откачка с внутренний точки соединения диверторной пластины с плазмой (the inner strike point) будет оптимизироваться для получения требуемой треугольности 4.9.2. Управление ELM В ИТЭР, управление в реальном времени сценарием ELM необходимо для смягчения их последствий (снижение тепловых нагрузок на дивертор и совместимость с ITB), управления примесями и топливом при этом сохраняя Wped для обеспечения горения плазмы. Два способа контроля ELM видны. Первый – это перевод ELM больших в маленькие, второй увеличить другие каналы потерь.

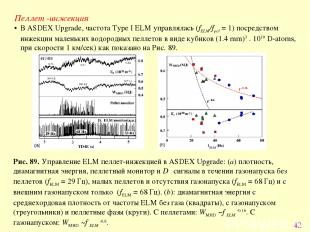
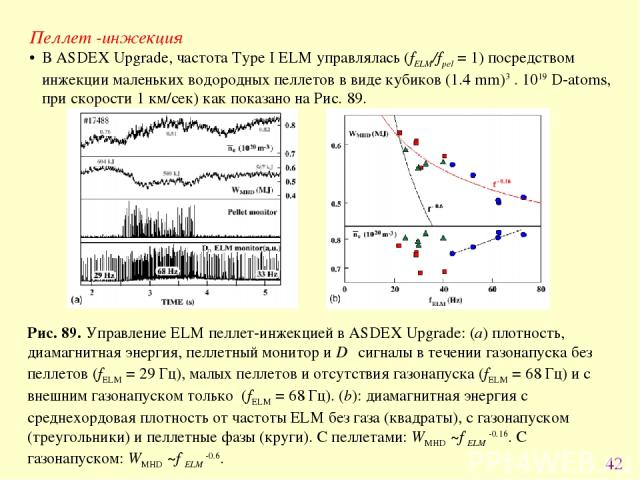
* Пеллет -инжекция В ASDEX Upgrade, частота Type I ELM управлялась (fELM/fpel = 1) посредством инжекции маленьких водородных пеллетов в виде кубиков (1.4 mm)3 . 1019 D-atoms, при скорости 1 км/сек) как показано на Рис. 89. Рис. 89. Управление ЕLM пеллет-инжекцией в ASDEX Upgrade: (a) плотность, диамагнитная энергия, пеллетный монитор и Dα сигналы в течении газонапуска без пеллетов (fELM = 29 Гц), малых пеллетов и отсутствия газонапуска (fELM = 68 Гц) и с внешним газонапуском только (fELM = 68 Гц). (b): диамагнитная энергия с среднехордовая плотность от частоты ELM без газа (квадраты), с газонапуском (треугольники) и пеллетные фазы (круги). С пеллетами: WMHD ~f ELM -0.16. С газонапуском: WMHD ~f ELM -0.6.

* Контроль граничного тока Изменение периферийного тока может модифицировать условия устойчивости и характеристики ELM как это предсказывается теорией the peeling–ballooning mode. На токамаке COMPASS-D, Type I ELMs тригеррировались когда ток пограничный увеличивался. В TCV, с использованием генерации положительного (вверх для LSN) тока при вертикальном смещении плазмы, ELMs тригеррировались также. Для приложения к ИТЭР такого способа, надо оценить эффекты ограниченных возможностей подвода мощности локально на периферию для создания дополнительного тока. Применение внешнего поля В JFT-2M, ELM-free H-mode делалась попытка ее перевода в стационарную ELMy H-mode путем прикладывания эргодического магнитного поля [Miura Y. et al 1991 Proc. 13th Int. Conf. on Plasma Physics and Controlled Nuclear Fusion Research (Washington, D.C., 1990) (Vienna: IAEA) vol 1 p 325]. Обнаружено, что компонента винтового поля с n = 4 эффективна для инициирования ELMs [687]. COMPASS-D также демонстрировал такой переход прикладывая радиальное магнитное возмущение на периферии плазмы. С другой стороны, на DIII-D [Evans T.E. et al 2004 Phys. Rev. Lett. 92 235003], Type I ELMs подавлялись почти полностью с внешними винтовыми магнитными возмущениями (в основном с n = 3 гармоникой при q95 = 3–4), при этом сохраняя свойства удержания плазмы. Для того, чтобы схему пограничной эргодизации применить к ИТЭР, необходимо изучение влияния такого способа на пьедестал, а также на стабильность low-n global mode при высоких бетта.

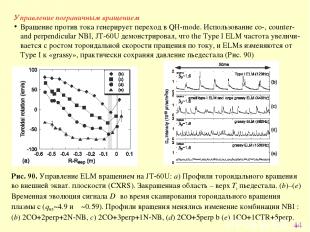
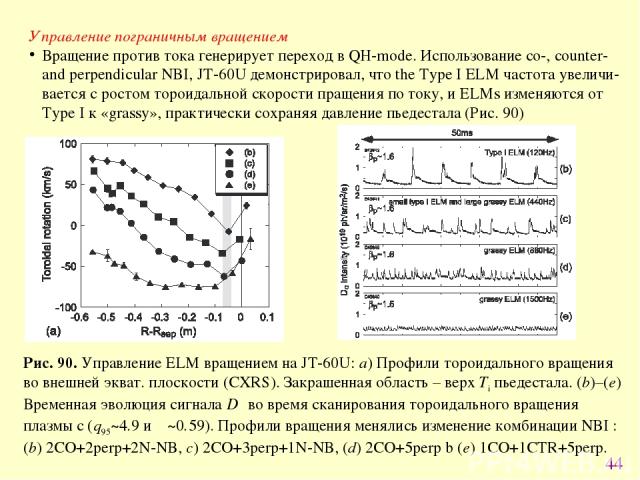
* Управление пограничным вращением Вращение против тока генерирует переход в QH-mode. Использование co-, counter- and perpendicular NBI, JT-60U демонстрировал, что the Type I ELM частота увеличи-вается с ростом тороидальной скорости пращения по току, и ELMs изменяются от Type I к «grassy», практически сохраняя давление пьедестала (Рис. 90) Рис. 90. Управление ЕLM вращением на JT-60U: a) Профили тороидального вращения во внешней экват. плоскости (CXRS). Закрашенная область – верх Ti пьедестала. (b)–(e) Временная эволюция сигнала Dα во время сканирования тороидального вращения плазмы с (q95~4.9 и δ ~0.59). Профили вращения менялись изменение комбинации NBI : (b) 2CO+2perp+2N-NB, c) 2CO+3perp+1N-NB, (d) 2CO+5perp b (e) 1CO+1CTR+5perp.

* Содержание лекции №4 «Динамика и перенос в пьедестале» 4.1. Режимы улучшенного удержания в Н-моде при высоких плотностях и операционных пределах 4.2. Структура и характеристики пьедестала 4.3. L-H переходы 4.4. Теория и моделирование переноса в пьедестале 4.5. Моделирование структуры пьедестала 4.6. Структура Type I ELM, эффекты на профилях пьедестала и техники смягчения 4.7. Альтернативы режиму «Type I ELMy H-mode» 4.8. Устойчивость пьедестала 4.9. Возможные сценарии управления пьедесталом 4.10. Выводы по теме «Динамика и перенос в пьедестале»

* Граничный пьедестал является ключевой областью, определяющей функционирование горящей стационарной плазмы. В ITER Physics Basis были идентифицированы следующие физические проблемы: (i) распространение режима улучшенного удержания для больших плотностей (~ nG); (ii) создание предсказательных возможностей для давления и радиальной структуры пьедестала в горящей плазме; (iii) смягчение амплитуд гигантских (Type I) ELM; (iv) разработка техники управления давлением пьедестала и ELMs. В решении этих задач был сделан существенный прогресс: (i) Режим улучшенного удержания для больших плотностей (~ nG) был реализован с помощью большой треугольности плазмы; (ii) Теория peeling–ballooning mode объяснила градиента давления в пьедестале в режиме «Type I ELM » и его вариации с изменением формы плазмы. Детальная структура ELM срыва (полоидальная ассиметрия, радиальное распределение и др.) были экспериментально выяснены; (iii)- (iv) Были открыты режимы без ELM и с малыми ELM и некоторые из них демонстрировались при низкой столкновительности. Было найдено, что треугольность формы, запас устойчивости, граничное вращение, столкновительность и гармонические осцилляции играют ключевую роль в этих режимах. Экспериментально показано наличие быстрых изменений в радиальном электрическом поле и порога в температурах и их градиентах для L–H перехода.

* Наконец, перечислим оставшиеся важные вопросы: Наиболее важной является проблема неопределенности в ширине граничного транспортного барьера. Несмотря на наличие мульти-машинной базы данных по структуре пьедестала, скейлинг для ширины не установлен. Для профиля плотности, эффекты нейтралов моделировались, но необходимо их более систематическое подтверждение Как это было сделано для работы вблизи предела Гринвальда по плотности, распространения в область малой столкновительнсти также необходимо. Для понимания динамики ELM срыва (их периода, например), нелинейная эволюция МГД неустойчивостей должна быть выяснена, также как и эволюция граничного профиля плотности тока и перенос во время ELM. Важны попытки распространить режимы без ELM и с малыми ELM для условий, соответствующих реактору. Важнейшим инструментом для решения вышеперечисленных проблем видится развитие диагностик периферийных профилей плотности тока.