Презентация на тему: Постулаты специальной теории относительности

СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (СТО) 1. Принцип относительности Галилея. Закон сложения скоростей 2. Постулаты Эйнштейна 3. Преобразования Лоренца 4. Следствия из преобразований Лоренца 5. Релятивистская механика 6. Взаимосвязь массы и энергии покоя 900igr.net

Принцип относительности Галилея. Закон сложения скоростей При изложении механики предполагалось, что механические явления происходят одинаково в двух системах отсчета, движущихся равномерно и прямолинейно относительно друг друга. Это есть принцип относительности Галилея

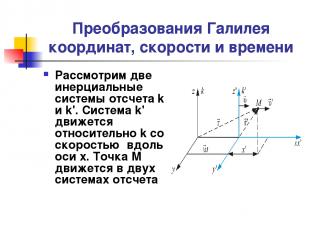
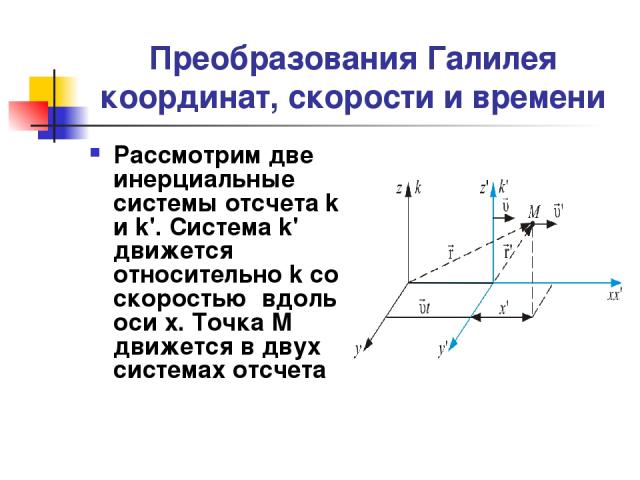
Преобразования Галилея координат, скорости и времени Рассмотрим две инерциальные системы отсчета k и k'. Система k' движется относительно k со скоростью вдоль оси x. Точка М движется в двух системах отсчета

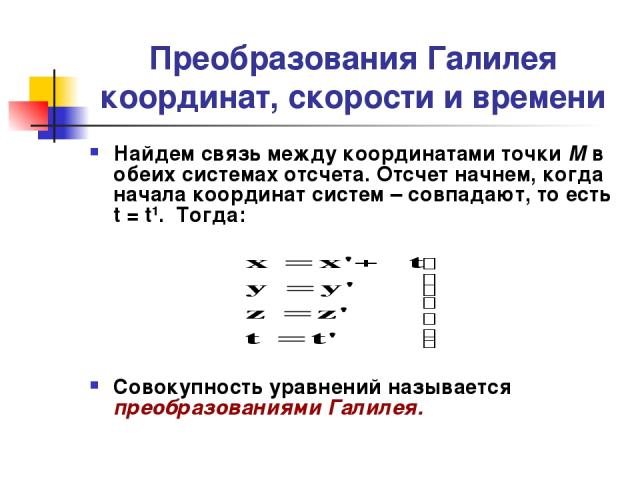
Преобразования Галилея координат, скорости и времени Найдем связь между координатами точки M в обеих системах отсчета. Отсчет начнем, когда начала координат систем – совпадают, то есть t = t1. Тогда: Совокупность уравнений называется преобразованиями Галилея.

Преобразования Галилея координат, скорости и времени В векторной форме преобразования Галилея можно записать так: Продифференцируем это выражение по времени, получим: Или Это выражение определяет закон сложения скоростей в классической механике.

Специальная теория относительности В 1905 г. в журнале «Анналы физики» вышла знаменитая статья А. Эйнштейна «К электродинамике движущихся тел», в которой была изложена специальная теория относительности (СТО). В основе СТО лежат два постулата выдвинутых Эйнштейном. 1. Все законы природы одинаковы во всех инерциальных системах отсчета. 2. Скорость света в пустоте одинакова во всех инерциальных системах отсчета и не зависит от скорости источника и приемника света.

Преобразования Лоренца Формулы преобразования при переходе из одной инерциальной системы в другую с учетом постулатов Эйнштейна предложил Лоренц в 1904 г. Лоренц Хендрик Антон (1853 – 1928) – нидерландский физик-теоретик, член многих академий наук, в том числе и АН СССР, лауреат Нобелевской премии.

Преобразования Лоренца Лоренц установил связь между координатами и временем события в системах отсчета k и k' основываясь на тех экспериментальных фактах, что: все инерциальные системы отсчета физически эквивалентны; скорость света в вакууме постоянна и конечна, во всех инерциальных системах отсчета и не зависит от скорости движения источника и наблюдателя.

Преобразования Лоренца Таким образом, при больших скоростях движения сравнимых со скоростью света, Лоренц получил: y = y, y, = y z = z, z, = z

Преобразования Лоренца Истинный физический смысл этих формул был впервые установлен Эйнштейном в 1905 г. в СТО. В теории относительности время иногда называют четвертым измерением. Точнее говоря, величина ct, имеющая ту же размерность, что и x, y, z ведет себя как четвертая пространственная координата. В теории относительности ct и x проявляют себя с математической точки зрения сходным образом.

Преобразования Лоренца При малых скоростях движения или при бесконечной скорости распространения взаимодействий ( теория дальнодействия) преобразования Лоренца переходят в преобразования Галилея (принцип соответствия).

Следствия из преобразований Лоренца Одновременность событий в СТО По Ньютону, если два события происходят одновременно, то это будет одновременно для любой системы отсчета (время абсолютно). Эйнштейн задумался, как доказать одновременность?

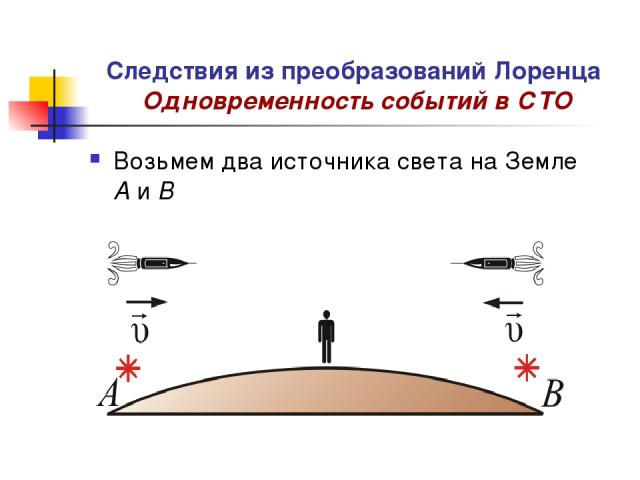
Следствия из преобразований Лоренца Одновременность событий в СТО Возьмем два источника света на Земле А и В

Следствия из преобразований Лоренца Одновременность событий в СТО Если свет встретится на середине АВ, то вспышки для человека находящегося на Земле, будут одновременны. Но со стороны пролетающих мимо космонавтов со скоростью υ вспышки не будут казаться одновременными, т.к. c=const . Рассмотрим это более подробно.

Следствия из преобразований Лоренца Одновременность событий в СТО Пусть в системе k (на Земле) в точках x1 и x2 происходят одновременно два события в момент времени t1=t2=t. Будут ли эти события одновременны в k' (в пролетающей мимо ракете)? Для определения координат в k' воспользуемся преобразованиями Лоренца.

Следствия из преобразований Лоренца Одновременность событий в СТО Получим:

Следствия из преобразований Лоренца Одновременность событий в СТО Если события в системе k происходят одновременно в одном и том же месте, то и т.е. и для k' эти события тоже одновременны.

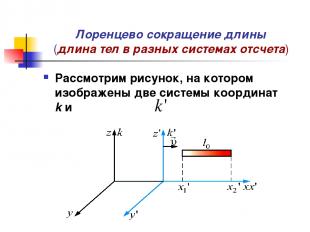
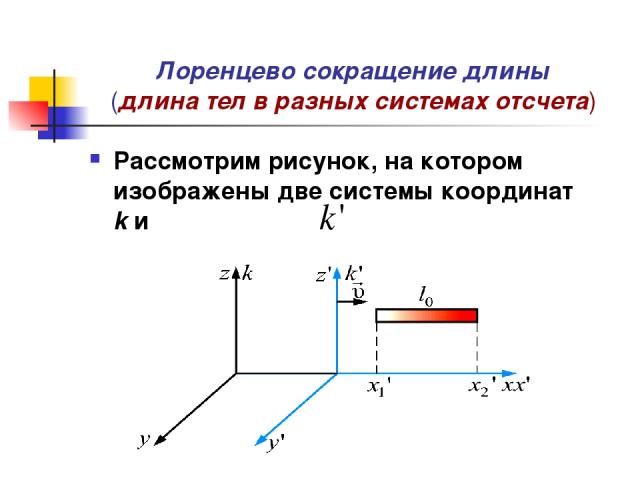
Лоренцево сокращение длины (длина тел в разных системах отсчета) Рассмотрим рисунок, на котором изображены две системы координат k и

Лоренцево сокращение длины (длина тел в разных системах отсчета) Пусть – собственная длина тела в системе, относительно которого тело неподвижно (например: в ракете движущейся со скоростью мимо неподвижной системы отсчета k (Земля)). Измерение координат x1 и x2 производим одновременно в системе k, т.е.

Лоренцево сокращение длины (длина тел в разных системах отсчета) Используя преобразования Лоренца, для координат получим: т.е. Формула называется Лоренцевым сокращением длины. Собственная длина тела, есть максимальная длина. Длина движущегося тела короче, чем покоящегося. Причем, сокращается только проекция на ось x, т.е. размер тела вдоль направления движения.

Замедление времени (длительность событий в разных системах отсчета) Пусть вспышка лампы на ракете длится , где -собственное время, измеренное наблюдателем, движущимся вместе с часами. Чему равна длительность вспышки ( ) с точки зрения человека находящегося на Земле, мимо которого пролетает ракета?

Замедление времени (длительность событий в разных системах отсчета) Из преобразований Лоренца имеем: или Из этого уравнения следует, что собственное время – минимально (движущиеся часы идут медленнее покоящихся). Таким образом, вспышка на Земле будет казаться длиннее. Этот вывод имеет множество экспериментальных подтверждений.

Сложение скоростей в релятивистской механике Пусть тело внутри космического корабля движется со скоростью Сам корабль движется с такой же скоростью . Чему равна скорость тела относительно Земли ?

Сложение скоростей в релятивистской механике Классическая механика Но скорость света является предельной скоростью переноса информации, вещества и взаимодействий: Оценим скорость тела, используя преобразования Лоренца.

Сложение скоростей в релятивистской механике Внутри корабля перемещение dx' за время dt' равно Найдем dx и dt с точки зрения наблюдателя на Земле, исходя из преобразований Лоренца: dy = dy'; dz = dz';

Сложение скоростей в релятивистской механике Так как , то: Эта формула выражает правило сложения скоростей в релятивистской кинематике для х – вой компоненты.

Сложение скоростей в релятивистской механике Для у – вой компоненты скорости, если движение частицы происходит не параллельно оси х, правило преобразования для и следующее: Тогда скорость частицы в системе К:

Релятивистская динамика Релятивистский импульс В векторной форме Релятивистское выражение для полной энергии

Релятивистская динамика При , в системе координат, где частица покоится, полная энергия равна энергии покоя: Полная энергия складывается из энергии покоя и кинетической энергии (К). Тогда

Релятивистская динамика Соотношение, связывающее полную энергию с импульсом частицы. Это выражение, связывающее энергию и импульс является инвариантом. Закон взаимосвязи массы и энергии покоя и стало символом современной физики.

Релятивистская динамика Основное уравнение динамики в релятивистском случае: Из этого уравнения следует, что вектор ускорения частицы, в общем случае, не совпадает по направлению с вектором силы.