Презентация на тему: Оптические свойства линз

Тема: «Оптические свойства системы линз, сложенных вплотную». Цель: Провести экспериментальное и теоретическое исследование оптических свойств линз, сложенных вплотную. 900igr.net

Вопросы для повторения. Какие характеристики сферической линзы Вы знаете? (устно) Сформулируйте уравнение Гаусса и величины, в него входящие. (устно) Нарисуйте номограмму для собирающей линзы и объясните, как ей пользоваться. (на доске) Нарисуйте номограмму для рассеивающей линзы и объясните, как ей пользоваться. (на доске) Как и какие стандартные лучи используют для построения изображения в собирающей линзе? (устно) Как и какие стандартные лучи используют для построения изображения в рассеивающей линзе? (устно) Нарисуйте прохождение произвольного луча через собирающую линзу. (на доске) Нарисуйте прохождение произвольного луча через рассеивающую линзу. (на доске) Как найти фокусное расстояние собирающей линзы с помощью линейки?

Оборудование. Шесть линз на подставках: две серого цвета – собирающие; две зеленого цвета – собирающие; две серого цвета – рассеивающие; Трибометр, используемый как поставка и как измерительная линейка; Металлический экран белого цвета.

Экспериментальное исследование. Измерьте фокусные расстояния F1 серых линз и F2 зеленых линз. Найдите их оптические силы D1 и D2. Запишите результат в тетради. Сложите вместе две серые линзы, измерьте их общее фокусное расстояние F11, найдите общую оптическую силу D11, запишите результаты в тетради. Какой можно сделать вывод? Сложите вместе две зеленые линзы, измерьте их общее фокусное расстояние F22, найдите общую оптическую силу D22, запишите результаты в тетради. Какой можно сделать вывод? Сложите вместе серую и зеленую линзы, измерьте их общее фокусное расстояние F12 и F21, найдите общую оптическую силу D12 и D21, запишите результаты в тетради. Какой можно сделать вывод?

Выводы: Фокусное расстояние системы двух одинаковых линз уменьшилось вдвое, а их оптическая сила увеличилась вдвое. Фокусное расстояние системы двух разных линз не зависит от порядка расположения линз и оказалось меньше наименьшего, а оптическая сила системы равна сумме оптических сил линз, составляющих систему. 1/F1 + 1/F2 = 1/F12 = 1/F21 D12 = D21 = D1 + D2

Обсуждение вывода Является ли этот вывод абсолютно верным? Мы не можем однозначно ответить на этот вопрос, так как точность наших вычислений невелика, и не потому, что мы пользовались сантиметровыми делениями, а потому, что наши линзы не идеально тонкие. Как можно проверить наш результат? Получить его теоретически для идеальных объектов – абсолютно тонких линз, каковые мы и изучаем.

Теоретическое исследование. Проверка с помощью номограмм. До сих пор мы рисовали номограммы для одной линзы. Как применить их к системе линз? Сделать это просто, если учесть, что f1 для первой линзы является d2 для второй, причем если f1 > 0, то d2 < 0 и наоборот. Найдя с помощью номограммы f1 мы перенесем её на ось 0d с помощью линии, направленной под углом 45о. Найдем f2 и соединим её с d1. Если под получившуюся линию подрисовать квадрат, одна вершина которого находится в начале координат, то его сторона и даст фокусное расстояние системы.

Проверка верности построения Как можно проверить верность построения? Посмотрим внимательно на уравнение связывающее фокусные расстояния линз: 1/F1 + 1/F2 = 1/F12 Какое уравнение оно напоминает? Уравнение Гаусса, в котором роль d играет F1, а роль f – F2. Каков физический смысл этого выражения? Если мы поместим источник в фокус первой линзы, то после прохождения пучка через неё он станет параллельным ГОО и, следовательно, сойдется в фокусе второй линзы. Поэтому, если провести линию, соединяющую фокусы, лежащие на разных осях, то она должна пройти через вершину квадрата, соответствующего общему фокусу.

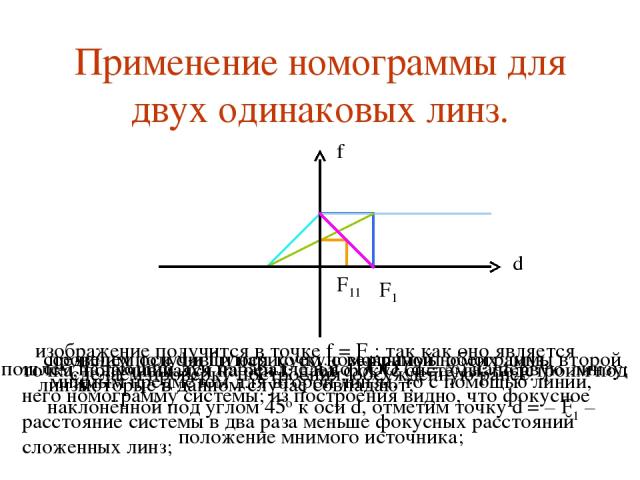
проведем оси d и f и нарисуем номограммы обеих линз, которые в данном случае совпадают; Применение номограммы для двух одинаковых линз. изображение получится в точке f = F1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы второй линзы; точка, получившаяся на оси f, даёт фокус системы; подстроим под него номограмму системы; из построения видно, что фокусное расстояние системы в два раза меньше фокусных расстояний сложенных линз; сделаем проверку построения, обсужденную ранее.
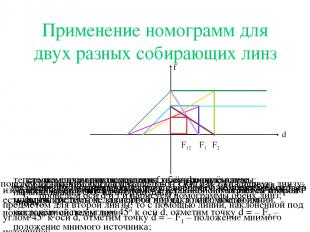
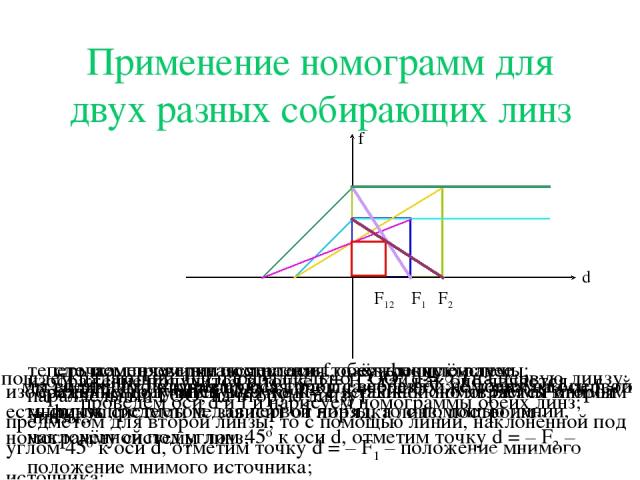
Применение номограмм для двух разных собирающих линз проведем оси d и f и нарисуем номограммы обеих линз; изображение получится в точке f = F1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы второй линзы; точка, получившаяся на оси f, даёт фокус системы; теперь поменяем линзы местами, то есть пошлём луч, параллельный ГОО, на вторую линзу; изображение получится в точке f = F2; так как оно является мнимым предметом для первой линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F2 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы первой линзы; сделаем проверку построения, обсужденную ранее. мы видим, что вторая прямая прошла через ту же точку на оси f, то есть фокус системы не зависит от порядка линз; построим номограмму системы линз;
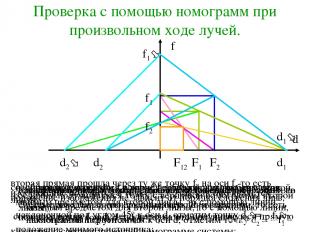
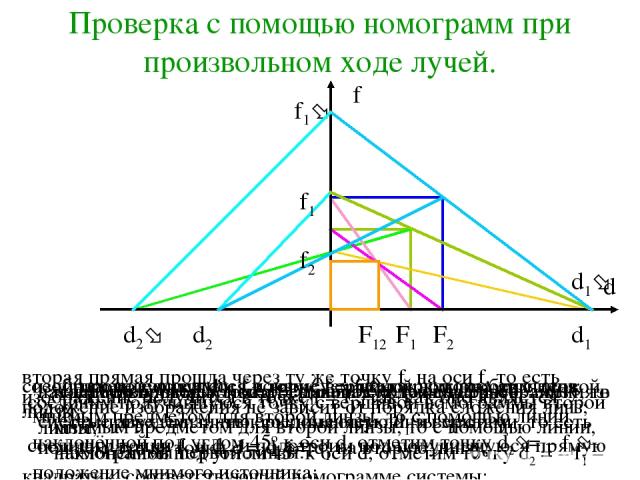
Проверка с помощью номограмм при произвольном ходе лучей. проведем оси d и f и нарисуем номограммы обеих линз; из произвольной точки d = d1 пошлём луч на первую линзу, то есть проведем линию, соединяющую d1 и вершину номограммы первой линзы. изображение получится в точке f = f1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d2 = – f1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы второй линзы; на оси f получилась точка f2, дающая положение изображения в системе двух линз; теперь поменяем линзы местами, то есть пошлём луч из точки d = d1 = d1 на вторую линзу; изображение получится в точке f = f1 ; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d2 = – f1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы первой линзы; вторая прямая прошла через ту же точку f2 на оси f, то есть положение изображения не зависит от порядка сложения линз; соединим точки f1 и d1, и подстроим под получившуюся прямую квадратик, соответствующий номограмме системы; сделаем проверку построения, обсужденную ранее.
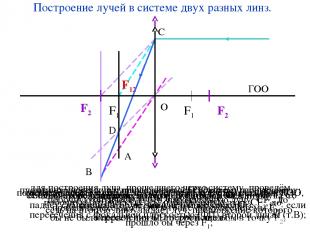
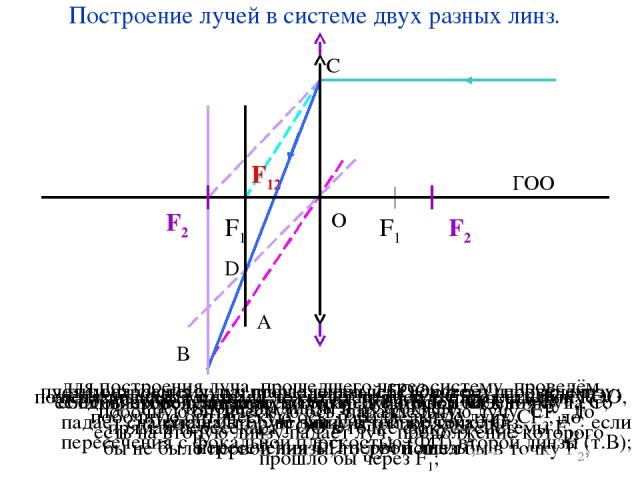
Построение лучей в системе двух разных линз. проведём главную оптическую ось (ГОО); изобразим линзы и их фокусы; пустим на систему луч, параллельный ГОО, через первую линзу; если бы второй линзы не было, то луч пошел бы в точку F1, то есть на вторую линзу падает луч, продолжение которого прошло бы через F1; для построения луча, прошедшего через систему, проведём побочную оптическую ось, параллельную лучу CF1, до пересечения с фокальной плоскостью (ФП) второй линзы (т.В); соединяем получившуюся точку B с точкой падения луча C; прямая пересекает ГОО в точке фокуса системы F12; поменяем линзы местами, то есть теперь луч, параллельный ГОО, падает сначала на вторую линзу в той же точке C; если бы не было первой линзы, то луч пошел бы в точку F2; для построения луча, прошедшего через систему, проведём побочную оптическую ось, параллельную лучу CF2, до пересечения ФП первой линзы; получившаяся точка D лежит на прямой BC, то есть фокус системы F12 не зависит от порядка линз.

Аналитический вывод оптической силы системы линз, сложенных вплотную. Выведем соотношение для общей оптической силы системы из уравнения Гаусса. Запишем его для первой линзы: 1/d1 + 1/f1 = D1 отсюда: 1/f1 = D1 – 1/d1 . Но d2 = – f1,, следовательно, уравнение Гаусса для второй линзы 1/d2 + 1/f2 = D2 примет вид: 1/d1 – D1 +1/f2 = D2 или: 1/d1 +1/f2 = D2 + D1 Так как d1 это d для всей системы, а f2 это f для всей системы, то мы получаем: 1/d +1/f = D2 + D1 = D, ч.т.д.

Обсуждение аналитического вывода Так как уравнение Гаусса справедливо для любых линз, то и полученное соотношение тоже справедливо для комбинации любых линз – как собирающих, так и рассеивающих. Поэтому, перейдем к рассмотрению рассеивающих линз.

Нахождение фокусного расстояния рассеивающей линзы Можно ли, опираясь на полученное соотношение, найти фокусное расстояние для рассеивающей линзы? Да, если сложить её с собирающей линзой большей оптической силы. Давайте с помощью номограмм проверим его справедливость для трех случаев: 1. Оптическая сила собирающей линзы больше оптической силы рассеивающей; 2. Меньше; 3. Равна.
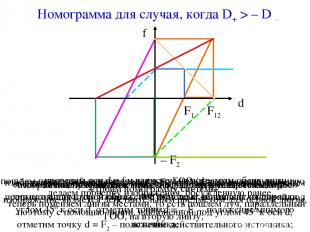
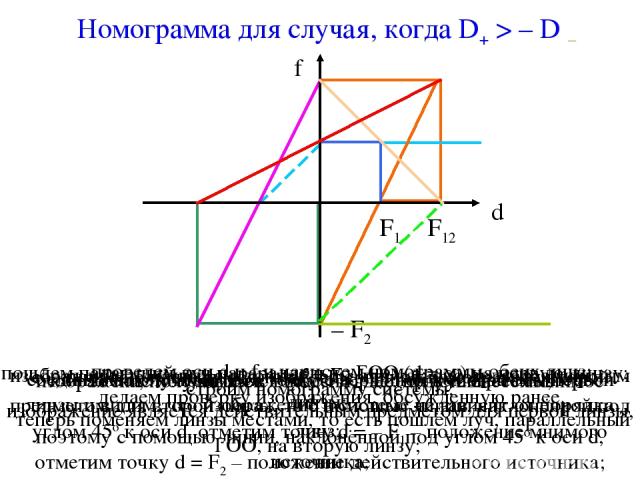
Номограмма для случая, когда D+ > – D – проведем оси d и f и нарисуем номограммы обеих линз; изображение получится в точке f = F1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы второй линзы; точка, получившаяся на оси f, даёт фокус системы; теперь поменяем линзы местами, то есть пошлём луч, параллельный ГОО, на вторую линзу; изображение получится в точке f = – F2; получившееся мнимое изображение является действительным предметом для первой линзы, поэтому с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = F2 – положение действительного источника; соединяем получившуюся точку с вершиной номограммы первой линзы и видим, что изображение в системе не зависит от порядка линз; строим номограмму системы; делаем проверку изображения, обсужденную ранее.
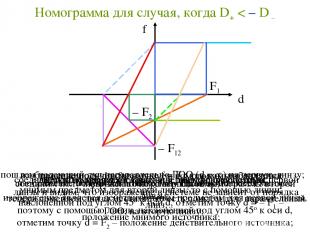
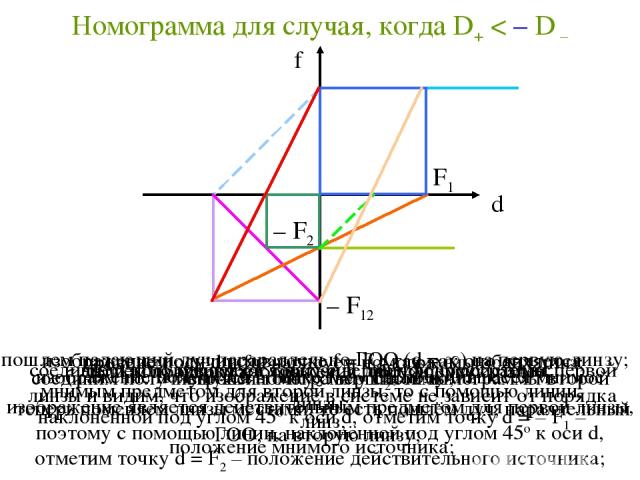
Номограмма для случая, когда D+ < – D – проведем оси d и f и нарисуем номограммы обеих линз; изображение получится в точке f = F1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F1 – положение мнимого источника; соединим получившуюся точку с вершиной номограммы второй линзы; точка, получившаяся на оси f, даёт фокус системы; теперь поменяем линзы местами, то есть пошлём луч, параллельный ГОО, на вторую линзу; изображение получится в точке f = – F2; получившееся мнимое изображение является действительным предметом для первой линзы, поэтому с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = F2 – положение действительного источника; соединяем получившуюся точку с вершиной номограммы первой линзы и видим, что изображение в системе не зависит от порядка линз; строим номограмму системы; делаем проверку изображения, обсужденную ранее.

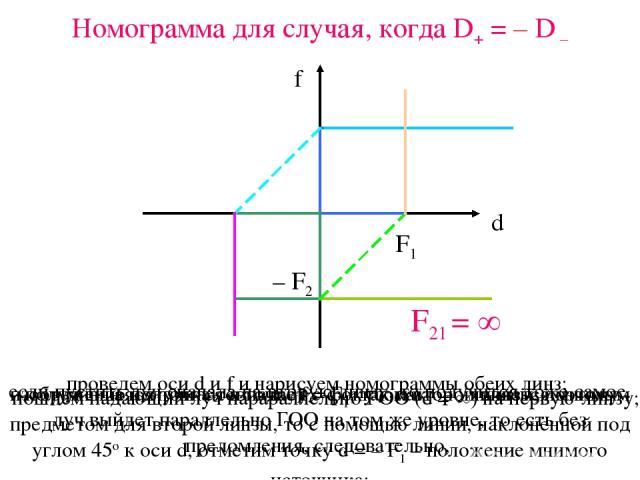
Номограмма для случая, когда D+ = – D – F21 = проведем оси d и f и нарисуем номограммы обеих линз; изображение получится в точке f = F1; так как оно является мнимым предметом для второй линзы, то с помощью линии, наклонённой под углом 45о к оси d, отметим точку d = – F1 – положение мнимого источника; получившаяся точка совпадает с фокусом второй линзы, поэтому луч выйдет параллельно ГОО на том же уровне, то есть без преломления, следовательно, если пустить луч сначала на вторую линзу, то получится тоже самое.

Выводы из построения номограмм В случае, когда D+ > – D– , мы получили систему с фокусным расстоянием > 0. В случае, когда D+ < – D– , мы получили систему с фокусным расстоянием < 0. В случае, когда D+ = – D– ,мы получили систему с фокусным расстоянием = , так как в систему вошел луч, параллельный ГОО, и на том же уровне снова вышел луч, параллельный ГОО.

Экспериментальное определение фокусного расстояния рассеивающей линзы. Давайте визуально сравним оптические силы имеющихся у нас собирающих линз с оптической силой рассеивающей линзы. Соединим вместе рассеивающую линзу с серой собирающей. Получается уменьшенное изображение, следовательно, – D– > D+. Соединим вместе рассеивающую линзу с зеленой собирающей. Получается какое-то искаженное, примерно равное изображение. По-видимому, их оптические силы почти равны. Как же экспериментально найти D– ? Надо соединить вместе две собирающие линзы и одну рассеивающую. Здесь возможны три комбинации: все серые линзы, две серые и одна зеленая, две зеленые и одна серая. Сейчас вы проделаете все измерения, а дома оформите это как лабораторную работу, включив в неё и предыдущие измерения.

Итоги. В результате нашего достаточно фундаментального исследования оптических свойств системы линз, сложенных вплотную, мы обнаружили, что оптическая сила системы равна алгебраической сумме оптических сил линз, входящих в систему: D = Di ; 1/F = 1/Fi Но, опираясь на высказывание Рене Декарта: «Главное метод, а не результат», можно считать, что главным результатом нашего урока, было приобретение навыков проведения научного исследования.

Домашнее задание. Оформить лабораторную работу. Сделать построение хода лучей для случаев собирающей и рассеивающей линз, разобранных на номограммах. Опираясь на чертеж построения лучей для двух разных собирающих линз, получить формулу 1/F1 + 1/F2 = 1/F12

Задачи. Точечный источник света помещен в фокусе рассеивающей линзы. Собирающая линза, приставленная вплотную к рассеивающей, превращает падающий на неё пучок лучей в параллельный. Найти отношение фокусных расстояний линз. Предмет расположен на расстоянии d = 18 см от плоско-выпуклой линзы с фокусным расстоянием F = 12 см. Выпуклая поверхность линзы обращена к предмету, плоская поверхность линзы посеребрена. На каком расстоянии f от линзы находится изображение предмета? Ученик привык читать книгу, держа её на расстоянии d = 20 см от глаза. Какова должна быть оптическая сила DОЧК очков, чтобы читать книгу, держа её на расстоянии наилучшего зрения d0 = 25 см? Дальнозоркий человек может читать книгу, держа её на расстоянии не менее d = 80 см от глаза. Какова должна быть оптическая сила DОЧК очков, чтобы читать книгу, держа её на расстоянии наилучшего зрения d0 = 25 см?

Получение соотношения 1/F12 = 1/F1 + 1/F2 из чертежа построения хода лучей в системе линз.