Презентация на тему: ксе

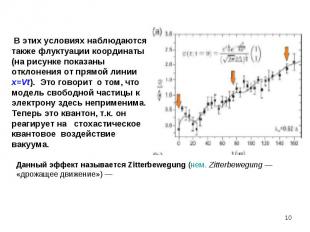
учет стохастических воздействий и вызываемых ими флуктуаций требует использования вероятностного описания природы. Это означает отказ от детерминистского взгляда на природу, который несовместим с понятием случайности.

Быть может, эти электроны – Миры, где пять материков, Искусства, знанья, войны, троны И память сорока веков. Еще, быть может, каждый атом – Вселенная, где сто планет; Там все, что здесь, в объеме сжатом, Но также то, чего здесь нет…. В. Брюсов. Мир ЭЛЕКТРОНА. Собр.соч. в 7-и тт. Т. 3. С. 172. М.: Худ. лит., 1974.

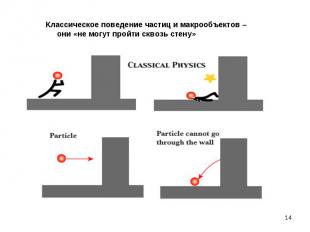
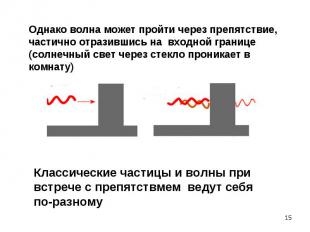
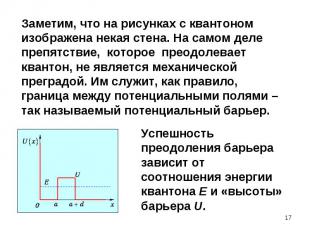
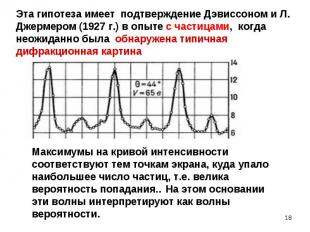
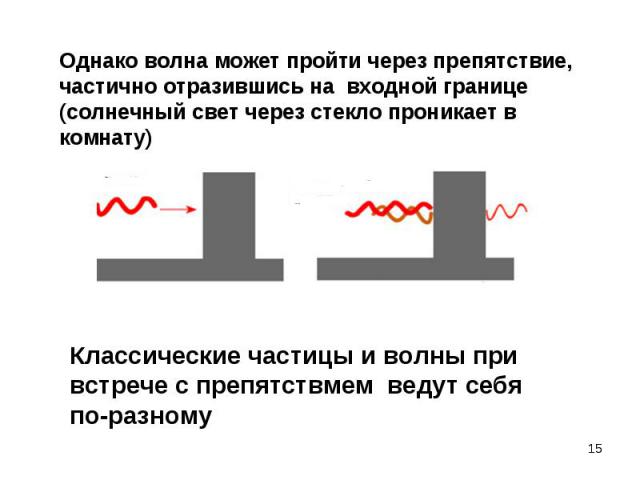
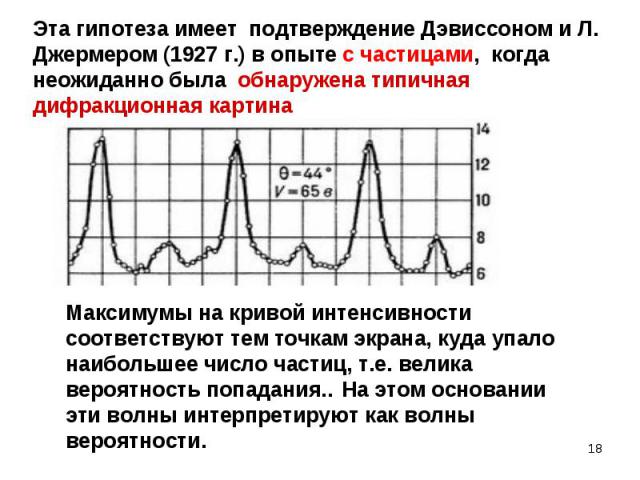
Дифракция - свидетельство особого волнового процесса, который в данном случае порождается движущимися частицами (напр., электронами) Дифракция - свидетельство особого волнового процесса, который в данном случае порождается движущимися частицами (напр., электронами) Природа этого процесса необычна (противоречивое сочетание волны и частицы, что невозможно в классике). Для интерпретации природы этих волн необходимо обсудить их особенности

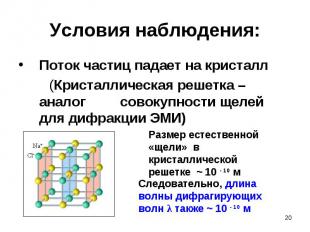
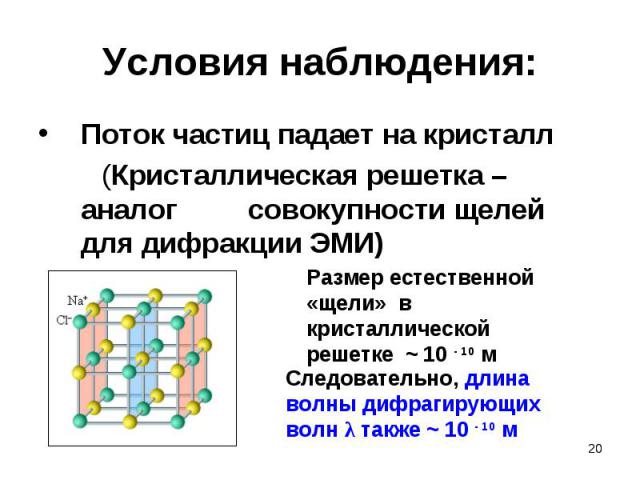
Поток частиц падает на кристалл Поток частиц падает на кристалл (Кристаллическая решетка – аналог совокупности щелей для дифракции ЭМИ)

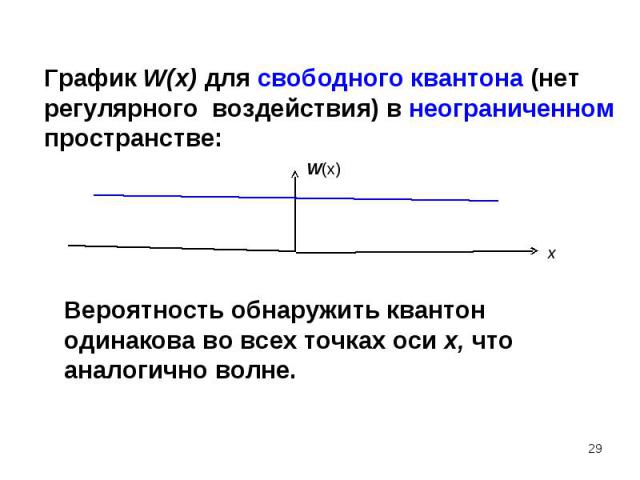
Эффект наблюдается для любых микрочастиц (с зарядом и нейтральных) Эффект наблюдается для любых микрочастиц (с зарядом и нейтральных) След., природа этого процесса не связана с электромагнитными волнами. Волновые свойства проявляются и у свободных (в классическом смысле) микрочастиц. След., природа этого процесса не связана с механическими волнами, т.е. с процессами, вызванными механическими возмущениями. Итак, экспериментально доказано, что при движении любых микрочастиц проявляются волновые свойства.

Волновые свойства возникают только в коллективе N одинаковых событий, происходящих в одних и тех же условиях Волновые свойства возникают только в коллективе N одинаковых событий, происходящих в одних и тех же условиях Этот коллектив называется неклассическим статистическим ансамблем Корректно использовать теорию вероятностей можно только в случае, когда N ∞.

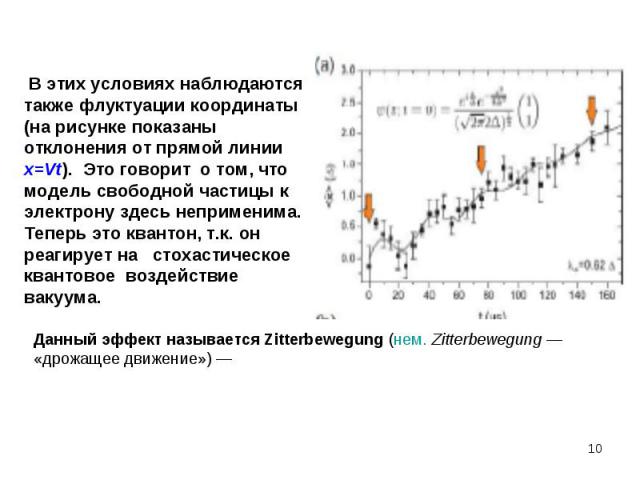
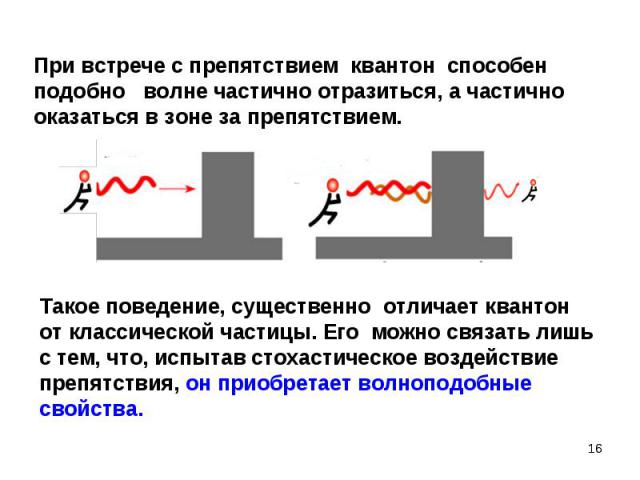
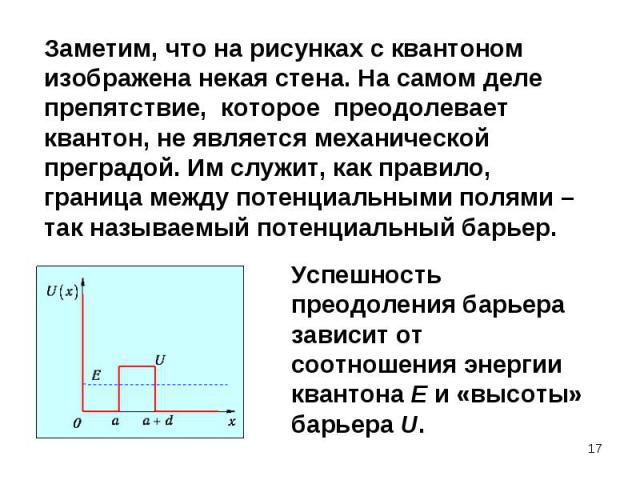
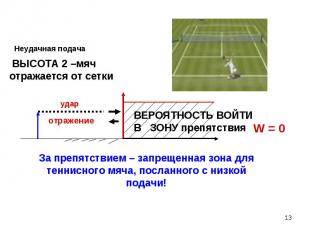
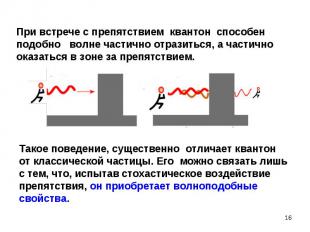
В момент прохождения условной «щели» частицы испытывают стохастическое квантовое воздействие В момент прохождения условной «щели» частицы испытывают стохастическое квантовое воздействие Возникает ансамбль квантонов и образуется дифракционная картина. Направление импульса (и скорости) квантона становится случайным. В случае ансамбля квантонов возникает устойчивая дифракционная картина

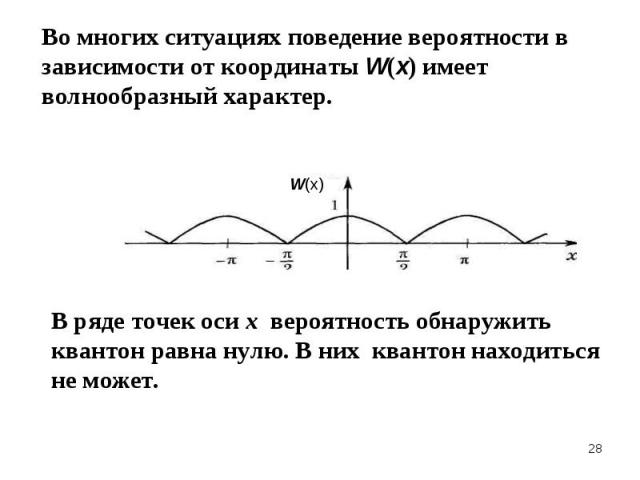
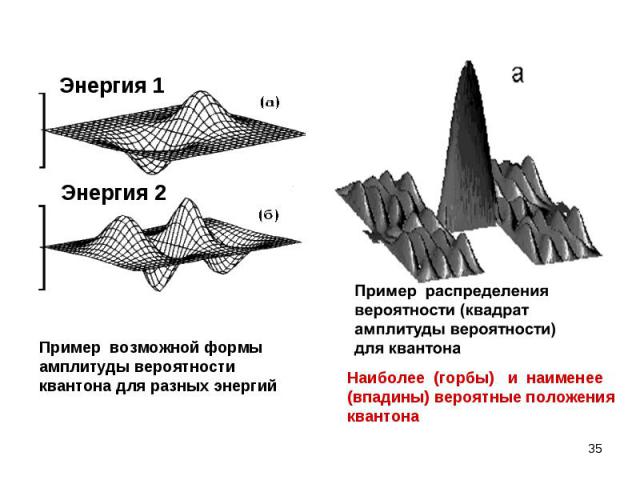
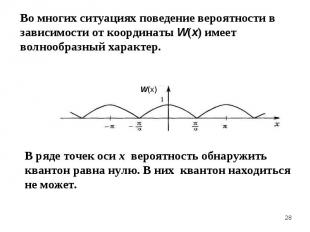
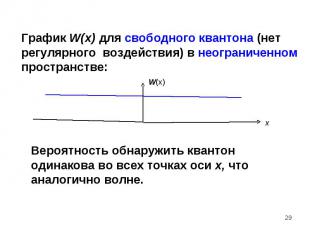
В опыте по дифракции одиночной микрочастицы на щели нельзя однозначно предсказать координату квантона х после прохождения щели. Это случайная характеристика. В опыте по дифракции одиночной микрочастицы на щели нельзя однозначно предсказать координату квантона х после прохождения щели. Это случайная характеристика. Координату квантона x после щели можно предсказать только через указание вероятности W(x) ее попадания в определенную точку экрана x , С помощью теории вероятностей для случайных величин находят средние значения характеристик и отклонения от них. Импульс и скорость способны испытывать флуктуации, характеризуемые дисперсией

Ансамбль квантонов описывается вероятностным образом через величину Ψ(x), называемую амплитудой вероятности, или волновой функцией. Она может быть комплекской функцией. Ансамбль квантонов описывается вероятностным образом через величину Ψ(x), называемую амплитудой вероятности, или волновой функцией. Она может быть комплекской функцией. Вероятность события W(х) , при котором одиночный квантон попадет в точку экрана с координатой х связана с амплитудой вероятности Ψ(x)| следующим соотношением: W(х) = |Ψ(x)|2 . Так как вероятность – действительная и сугубо положительная величина, в этой формуле амплитуда вероятности берётся по модулю: |Ψ(x)|2 = Ψ*(x) Ψ(x), где символ * означает комплексное сопряжение

1. Определить из опыта; 1. Определить из опыта; 2. Вычислить теоретически, решая знаменитое уравнение, предложенное Э.Шредингером.

позволяет непосредственно найти волновую функцию Ψ(x) квантона, а через нее и вероятность W(x) для целого ряда конкретных ситуаций позволяет непосредственно найти волновую функцию Ψ(x) квантона, а через нее и вероятность W(x) для целого ряда конкретных ситуаций Для квантовых состояний уравнение Шредингера играет роль, аналогичную роли уравнения второго закона Ньютона в классической физике.

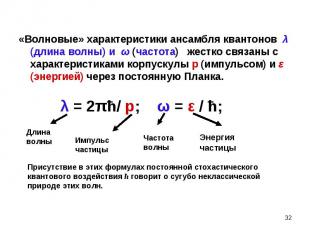
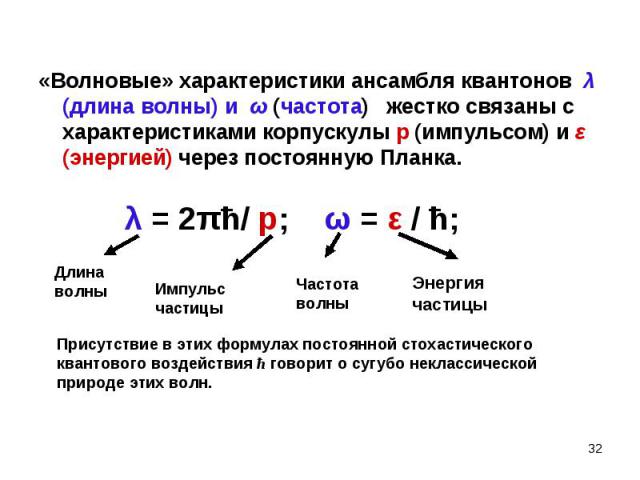
«Волновые» характеристики ансамбля квантонов λ (длина волны) и ω (частота) жестко связаны с характеристиками корпускулы р (импульсом) и ε (энергией) через постоянную Планка. «Волновые» характеристики ансамбля квантонов λ (длина волны) и ω (частота) жестко связаны с характеристиками корпускулы р (импульсом) и ε (энергией) через постоянную Планка.

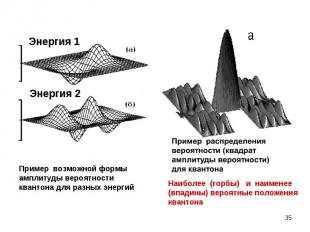
Квантон может одновременно находиться в нескольких квантовых состояниях: и в состоянии |1› и в состоянии |2›: состояние |3› = C1 |1› + C2 |2›; Квантон может одновременно находиться в нескольких квантовых состояниях: и в состоянии |1› и в состоянии |2›: состояние |3› = C1 |1› + C2 |2›; возникает «смесь» (суперпозиция) состояний, осуществляемых с разными вероятностями: W1 =|C1|2 ; W2 =|C2|2

квантон может одновременно находиться в разных точках пространства : и здесь, и там, и сям. квантон может одновременно находиться в разных точках пространства : и здесь, и там, и сям. Одновременное сочетание нескольких альтернативных возможностей – признак неклассической логики Логика «и-и» (идея дополнительности!)

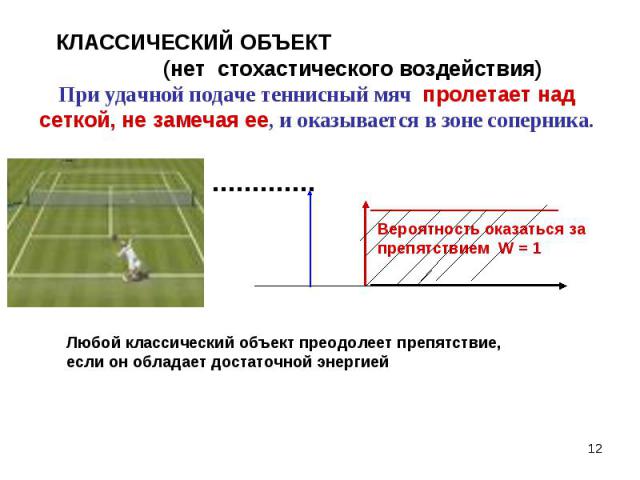
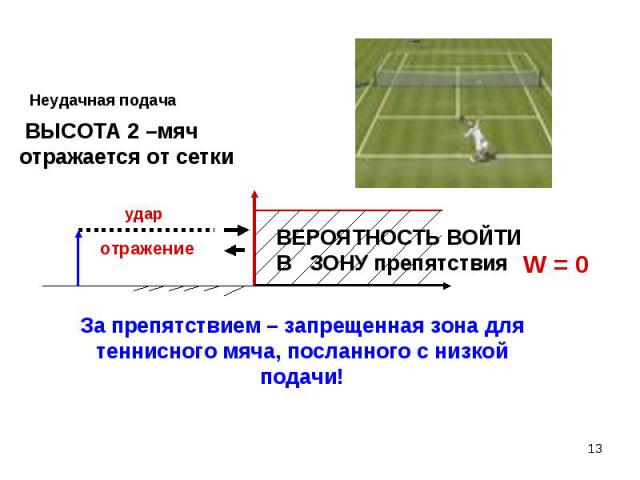
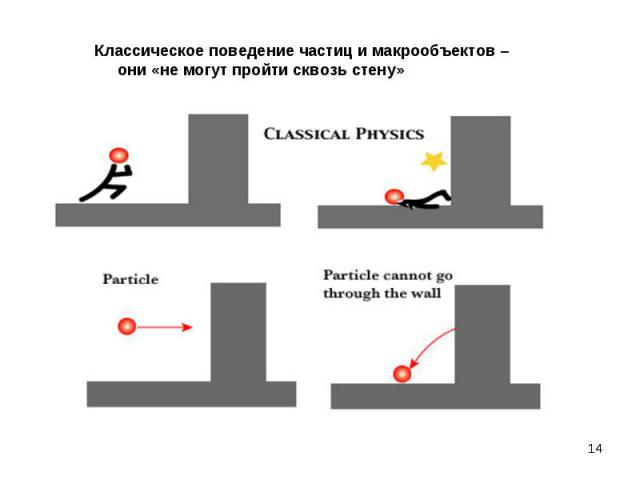
Всегда есть альтернатива: Всегда есть альтернатива: или здесь, или там Классическая логика основана на выборе одной из альтернативных возможностей. Это логика или-или

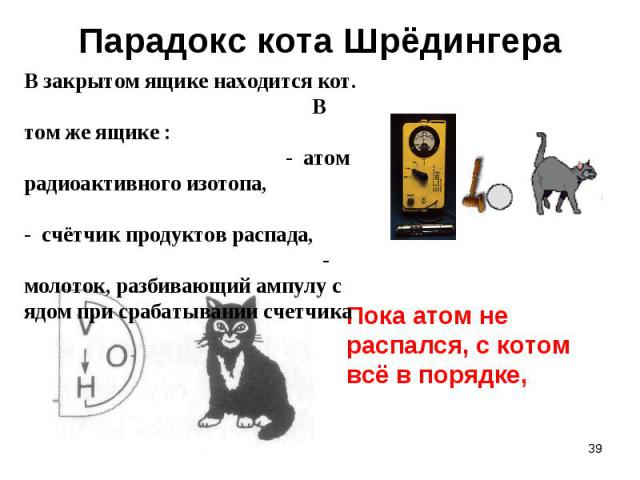
Неизвестно, когда атом распадётся. В каждый данный момент имеется лишь определённая вероятность его распада. Неизвестно, когда атом распадётся. В каждый данный момент имеется лишь определённая вероятность его распада. В каждый данный момент атом находится в суперпозиции двух квантовых состояний: состояния, когда он ещё не распался, и состояния, когда он уже распался.

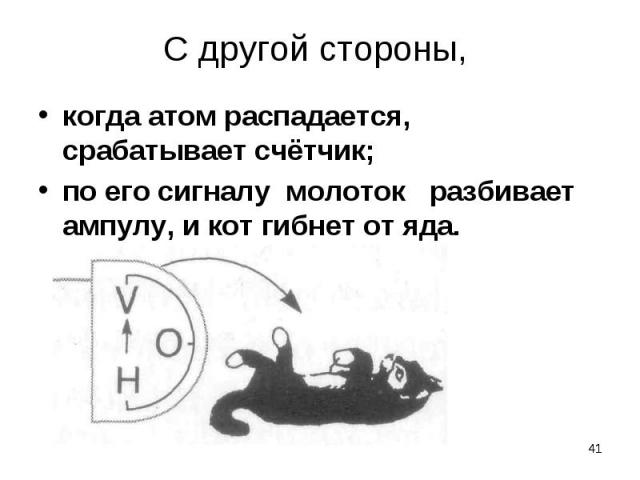
когда атом распадается, срабатывает счётчик; когда атом распадается, срабатывает счётчик; по его сигналу молоток разбивает ампулу, и кот гибнет от яда.

подходя к закрытому ящику, мы должны считать, что система (атом- кот) находится в суперпозиции двух состояний: подходя к закрытому ящику, мы должны считать, что система (атом- кот) находится в суперпозиции двух состояний:

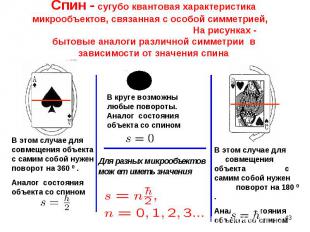
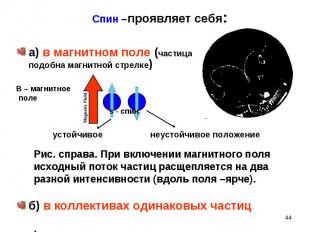
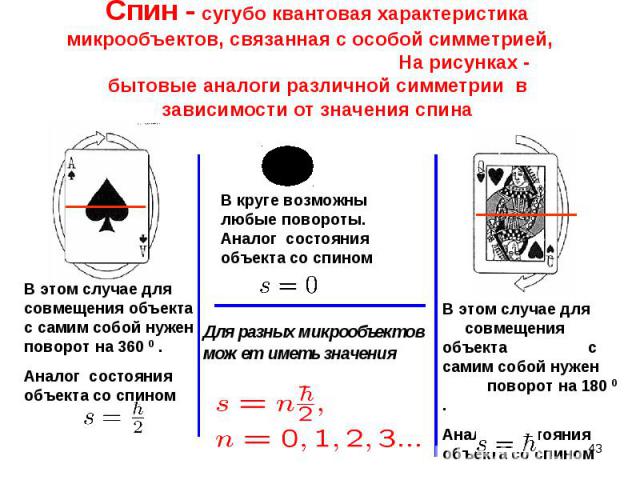
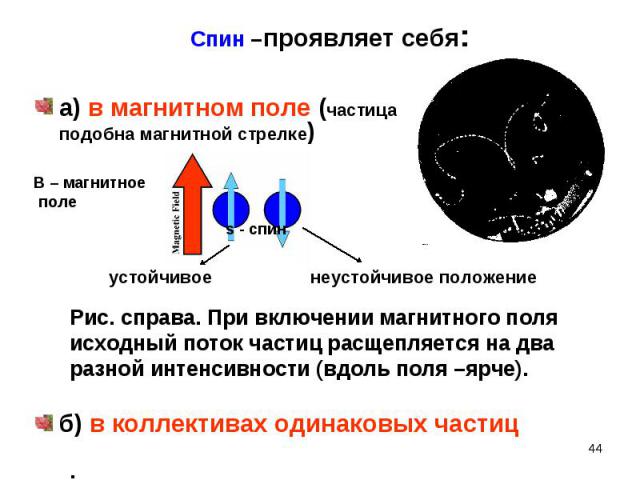
а) в магнитном поле (частица подобна магнитной стрелке) а) в магнитном поле (частица подобна магнитной стрелке) устойчивое неустойчивое положение б) в коллективах одинаковых частиц

бозоны (фотоны и другие переносчики фунламентальных взаимодействий с нулевой массой): бозоны (фотоны и другие переносчики фунламентальных взаимодействий с нулевой массой): s = 0, 1ħ, 2ħ, любое чётное число ħ/2 . фермионы (электроны, протоны, нейтроны и другие частицы с ненулевой массой): s = ½ ħ, 3/2 ħ, 5/2 ħ, …. (любое нечётное число ħ/2) - Различие между фермионами и бозонами проявляется в коллективном поведении тождественных квантонов.

Два и более фермиона с полностью идентичными характеристиками не могут одновременно находиться в одном квантовом состоянии! – принцип запрета Паули Два и более фермиона с полностью идентичными характеристиками не могут одновременно находиться в одном квантовом состоянии! – принцип запрета Паули

Если всё-таки все известные характеристики фермионов в одном состоянии совпадают, необходимо вводить новую характеристику, по которой между фермионами будет отличие! Если всё-таки все известные характеристики фермионов в одном состоянии совпадают, необходимо вводить новую характеристику, по которой между фермионами будет отличие! Пример 1. Для различения в нуклоне практически идентичных состояний трех кварков (фермионов) вводится новая трёхзначная характеристика – «цвет» (красный, синий, зелёный) (см. модель нуклона) Пример 2. Для различения в ядре дейтрона идентичных состояний протона и нейтрона (двух фермионов) вводится новая двузначная характеристика изоспин (±). Это позволяет глубже проникнуть в свойства микромира

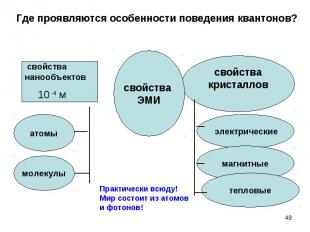
свойства свойства нанообъектов 10 - 9 м

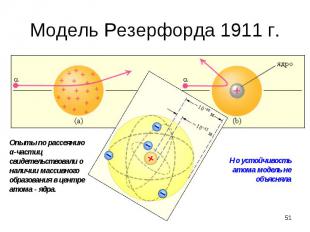
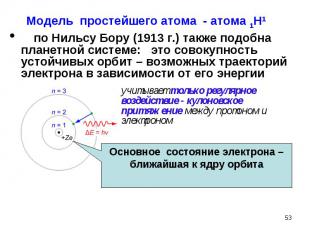
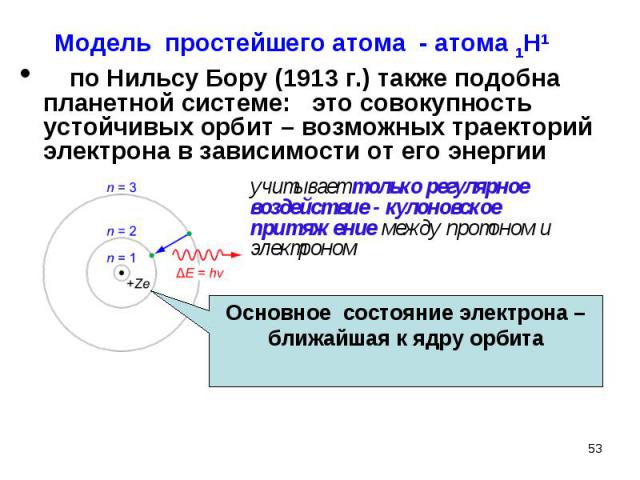
по Нильсу Бору (1913 г.) также подобна планетной системе: это совокупность устойчивых орбит – возможных траекторий электрона в зависимости от его энергии по Нильсу Бору (1913 г.) также подобна планетной системе: это совокупность устойчивых орбит – возможных траекторий электрона в зависимости от его энергии

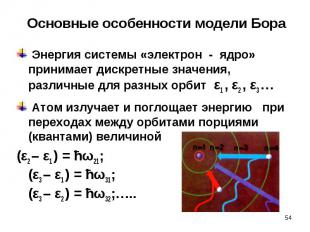
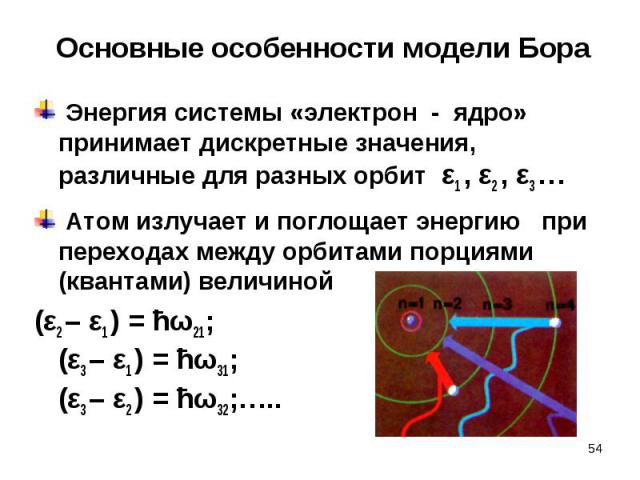
Энергия системы «электрон - ядро» принимает дискретные значения, различные для разных орбит ε1 , ε2 , ε3 … Энергия системы «электрон - ядро» принимает дискретные значения, различные для разных орбит ε1 , ε2 , ε3 … Атом излучает и поглощает энергию при переходах между орбитами порциями (квантами) величиной (ε2 – ε1 ) = ћω21; (ε3 – ε1 ) = ћω31; (ε3 – ε2 ) = ћω32;…..

– использует понятие электронной орбиты (определенной траектории) с постоянной энергией. – использует понятие электронной орбиты (определенной траектории) с постоянной энергией. но движение по ней должно сопровождаться потерей энергии на излучение, однако модель этого не учитывает - модель непоследовательна Волновые свойства электрона учитывает только косвенно - на орбите укладывается целое число стоячих волн де Бройля, однако рассматривается только дискретная совокупность разрешенных орбит

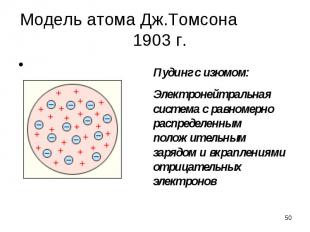
- учитывает только регулярное воздействие - кулоновское притяжение между протоном и электроном (классический подход), - учитывает только регулярное воздействие - кулоновское притяжение между протоном и электроном (классический подход), приписывает электрону дискретные значения энергии (противоречит классике!) не объясняет многие свойства атомов, наблюдаемые на опыте (в том числе – разнообразие геометрии и наличие объема).

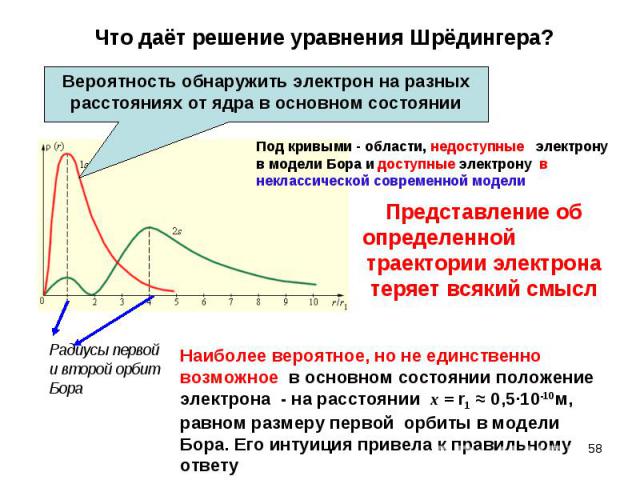
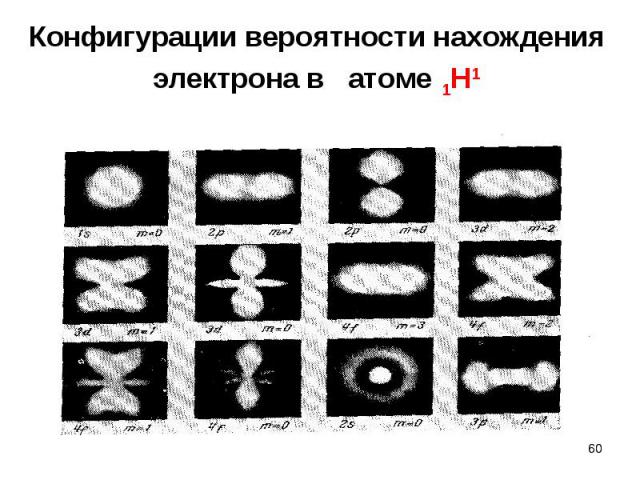
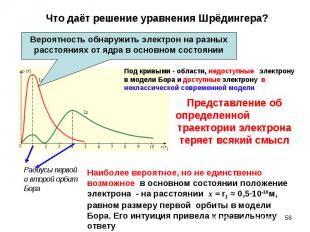
ОСОБЕННОСТИ: ОСОБЕННОСТИ: Учитывает стохастическое воздействие на электрон со стороны ядра Электрон - квантон даже в основном состоянии, он адекватно описывается волновой функцией Электрон может быть обнаружен практически на любом расстоянии от ядра, но с разной вероятностью

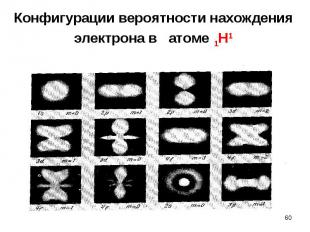
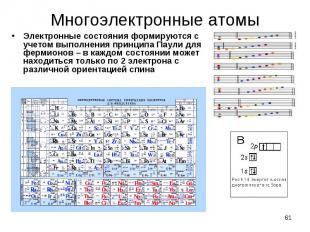
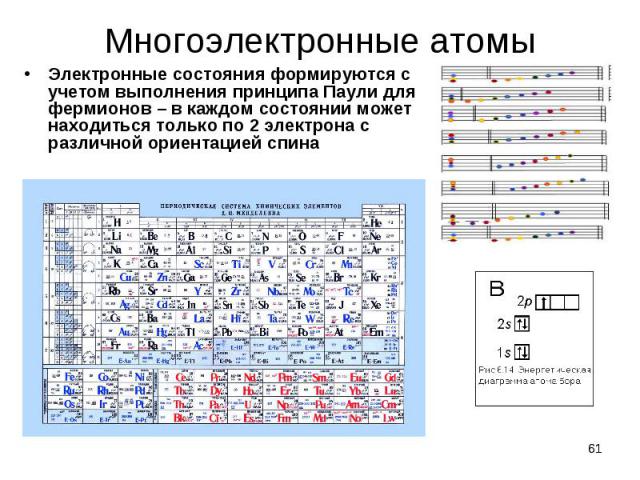
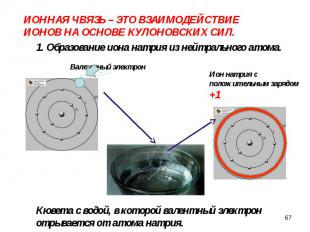
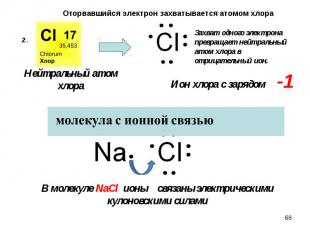
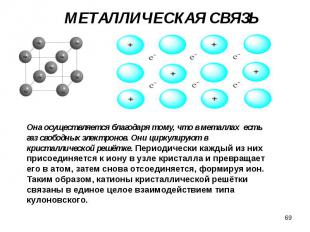
Электронные состояния формируются с учетом выполнения принципа Паули для фермионов – в каждом состоянии может находиться только по 2 электрона с различной ориентацией спина Электронные состояния формируются с учетом выполнения принципа Паули для фермионов – в каждом состоянии может находиться только по 2 электрона с различной ориентацией спина

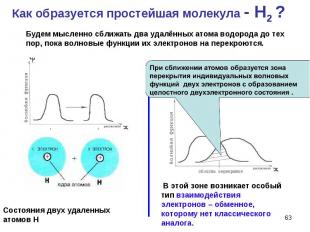
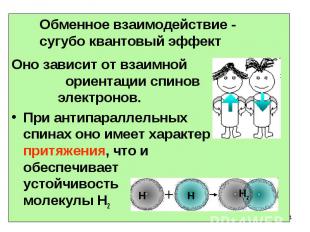
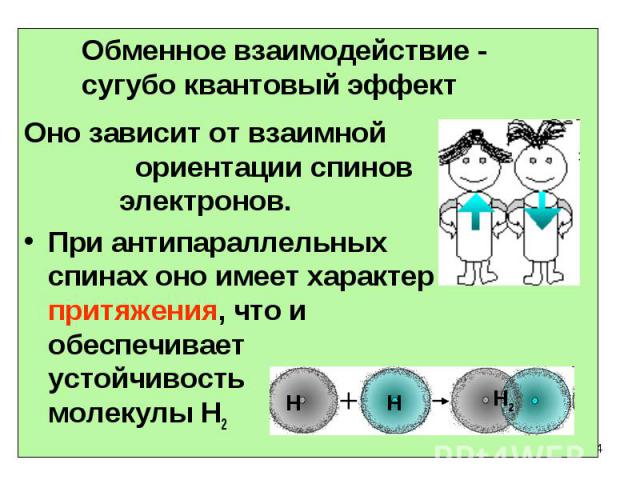
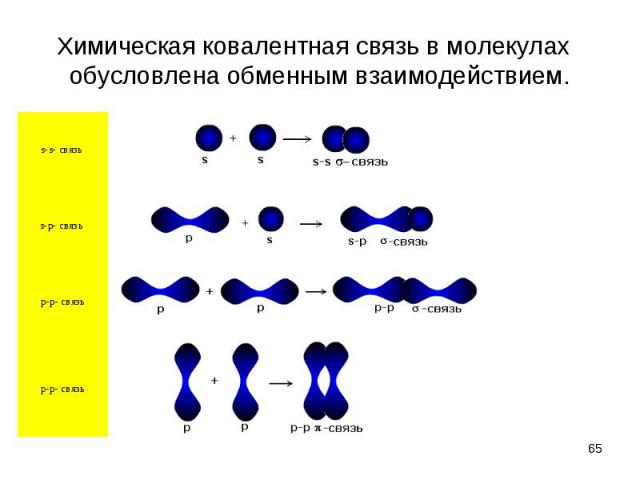
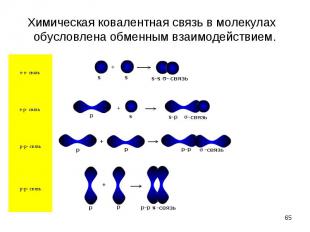
Оно зависит от взаимной ориентации спинов электронов. При антипараллельных спинах оно имеет характер притяжения, что и обеспечивает устойчивость молекулы Н2

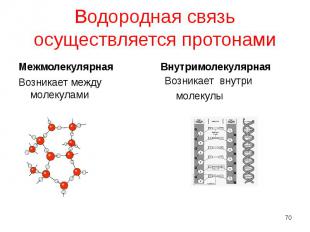
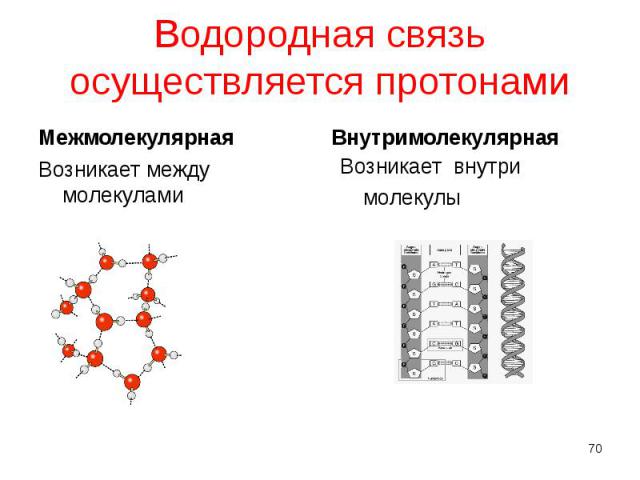
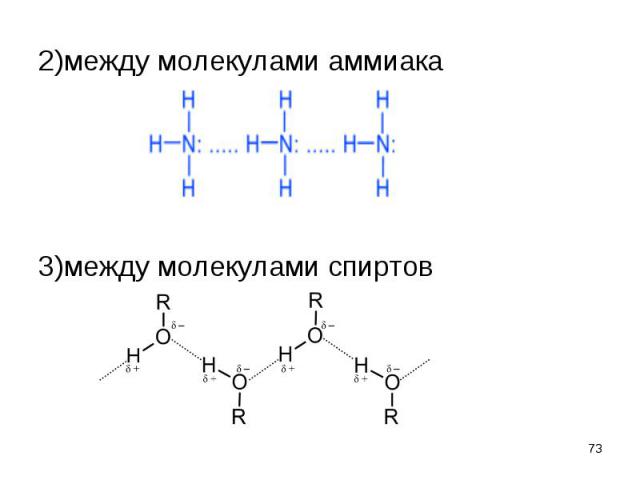
Межмолекулярная Межмолекулярная

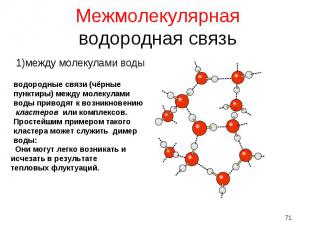
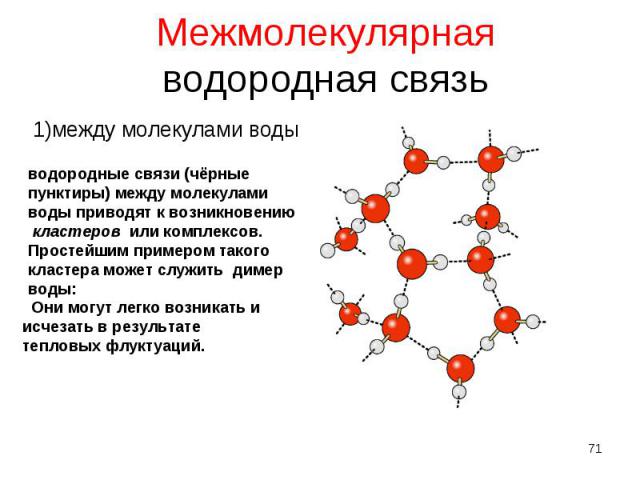
1)между молекулами воды 1)между молекулами воды

Межмолекулярные водородные связи способствуют образованию кристаллов в виде снежинок или измороси Межмолекулярные водородные связи способствуют образованию кристаллов в виде снежинок или измороси

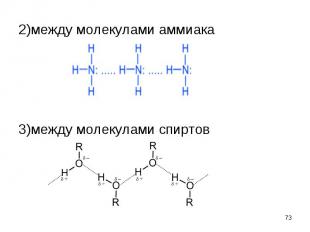
возникает возникает 1)внутри молекул белков (водородная связь удерживает витки спирали пептидной молекулы)