Презентация на тему: Компьютерные модели

Применение компьютерных моделей на уроке физики Из опыта работы И.В. Алешиной учителя физики МОУ СОШ № 17 г. Саров 2007 900igr.net

Компьютерные программы обучающие программы; демонстрационные программы; компьютерные модели; компьютерные лаборатории; лабораторные работы; пакеты задач; контролирующие программы; компьютерные дидактические материалы.

А нужен ли компьютер на уроке? Применение компьютерных технологий в образовании оправдано только в тех случаях, в которых возникает существенное преимущество по сравнению с традиционными формами обучения. Одним из таких случаев является преподавание физики с использование компьютерных моделей.

Компьютерные модели в школьном курсе

КОМПЬЮТЕРНАЯ МОДЕЛЬ – программа, которая позволяет имитировать физические явления, эксперименты или идеализировать ситуации, встречающиеся в задачах

В чем преимущества компьютерной модели перед натурным экспериментом ?

Воспроизведение тонких деталей; Не реальное явление, а его модель; Включение поэтапных факторов, усложняющих модель; Варьирование временного масштаба событий; Моделирование ситуаций, не реализуемых в реальном эксперименте

Современные программно-педагогические средства обучения физике развиваются с калейдоскопической быстротой

Нетрадиционные виды учебной деятельности учащихся Урок решения задач с последующей компьютерной проверкой. Урок - исследование. Урок - компьютерная лабораторная работа.

Методика использования компьютерных моделей на уроках

Максимальный учебный эффект, если: Составить план работы с выбранной для изучения компьютерной моделью; Сформулировать вопросы и задачи, согласованные с функциональными возможностями модели; Предупредить учащихся, что им в конце урока будет необходимо ответить на вопросы; Раздать индивидуальные задания в распечатанном виде .

Ознакомительные Компьютерные эксперименты Экспериментальные задачи Расчётные задачи с последующей компьютерной проверкой Неоднозначные задачи Задачи с недостающими данными Творческие задания Исследовательские задания Проблемные задания Качественные задачи Виды заданий

Как начинать работать с компьютерным курсом

Как проводить первые уроки в компьютерном классе на первых уроках в компьютерном классе желательно присутствие, особенно в течении первых 10-15 минут, учителя информатики; начинать с фрагмента урока длительностью не более 10-15 минут; вопросы и задания к моделям заранее распечатать и раздать учащимся в начале урока; длительность работы за компьютерами не должна превышать 30 минут, так как они обязательно должны в конце урока оформить небольшой отчёт; на первых уроках, возможно, следует выделять учащимся время на не запланированные вами эксперименты; Обсудите вопросы: · Какие модели с их точки зрения самые интересные? · Что они узнали нового, поработав с той или иной моделью? · Какие опыты они поставили и какие получили результаты?

Если вы смелый и решительный учитель, то можете сразу попытаться провести целый урок в компьютерном классе. Но…

Как составлять задания к компьютерным моделям

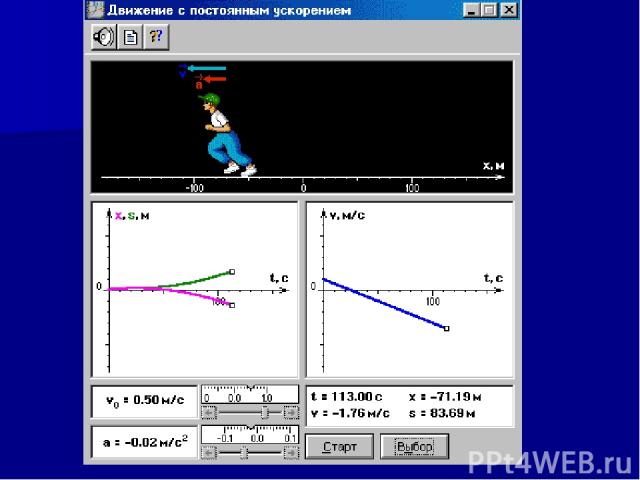
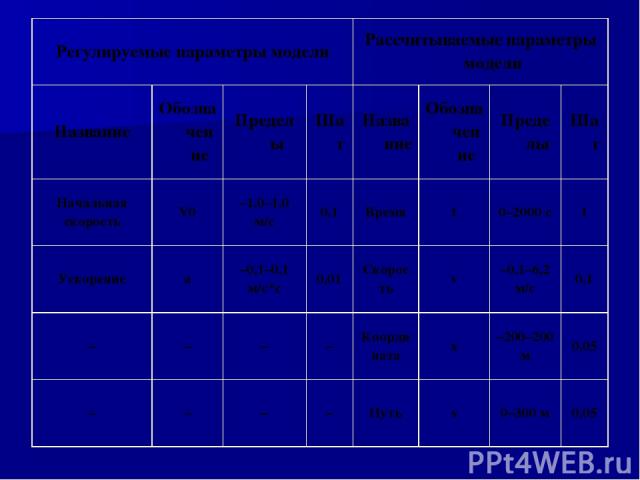
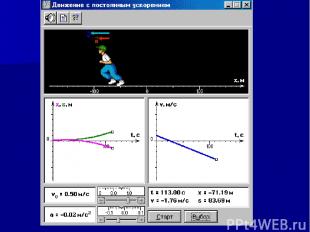
Таблица 1. Параметры модели "Движение с постоянным ускорением". Составьте таблицу для параметров модели: Регулируемые и расчитываемые. Для каждого параметра определите: Название; Обозначение; Пределы; Шаг.

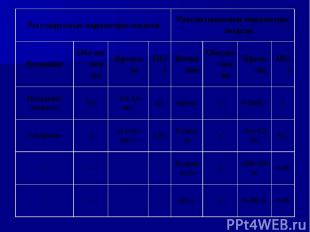
Регулируемые параметры модели Рассчитываемые параметры модели Название Обозначение Пределы Шаг Название Обозначение Пределы Шаг Начальная скорость V0 –1,0–1,0 м/с 0,1 Время t 0–2000 с 1 Ускорение a –0,1–0,1 м/c*c 0,01 Скорость v –0,1–6,2 м/c 0,1 – – – – Координата x –200–200 м 0,05 – – – – Путь s 0–300 м 0,05

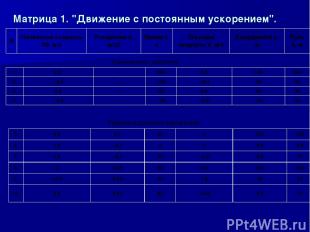
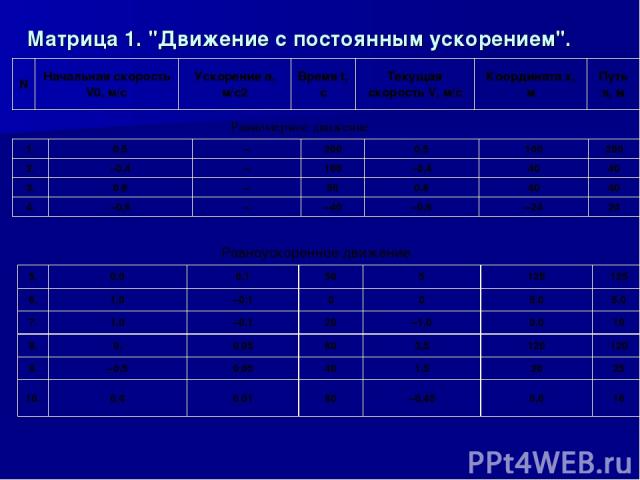
Матрица 1. "Движение с постоянным ускорением". Равномерное движение Равноускоренное движение N Начальная скорость V0, м/с Ускорение a, м/с2 Время t, с Текущая скорость V, м/с Координата x, м Путь s, м 1. 0,5 – 200 0,5 100 200 2. –0.4 – 100 –0,4 40 40 3. 0,8 – 50 0,8 40 40 4. –0,6 – –40 –0,6 –24 24 5. 0,0 0,1 50 5 125 125 6. 1,0 –0,1 0 0 5,0 5,0 7. 1,0 –0,1 20 –1,0 0,0 10 8. 0, 0,05 60 3,5 120 120 9. –0,5 0,05 40 1,5 20 25 10. 0,4 0,01 80 –0,45 0,0 16

Задания к модели «Движение с постоянным ускорением»

Задание N1. Откройте в разделе "Механика" тему "Равноускоренное движение". Установите параметр а = 0 м/с2. Нажмите кнопку "Начальн. Скорость" и установите величину скорости человечка. Нажмите кнопку "Старт" и посмотрите, что происходит на экране. Какие графики строит компьютер? Выясните, что означает знак " – " перед значением скорости. Что происходит при изменении знака скорости? Какие графики Вы наблюдали на экране компьютера?

Задание N2. Выполните компьютерный эксперимент. Установите V = –0,25 м/с, проведите эксперимент и ответьте на вопросы: Как выглядит график координаты? Какова координата человечка при t = 0? Какова координата человечка через 4 с? Какова координата человечка через 8 с? Как выглядит график пути? Как выглядит график скорости? Изменяется ли скорость при движении человечка? Как называется такое движение?

Задание N3. Постройте графики скорости, координаты и пути человечка, если он начинает движение из начала координат, а скорость его движения составляет –0.5 м/с. Проведите компьютерный эксперимент и проверьте Ваши ответы.

Задание N4. Придумайте задачу, решите её, поставьте компьютерный эксперимент и проверьте полученные результаты.

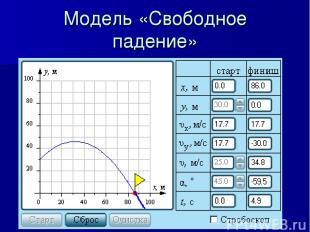
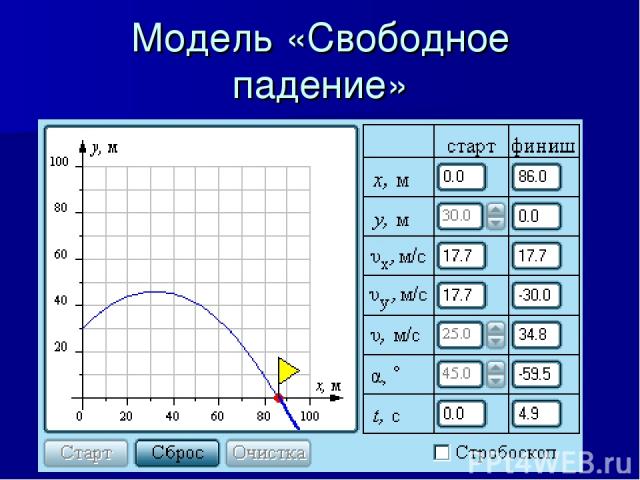
Модель «Свободное падение»

Таблица 2. Параметры модели "Свободное падение тел". Регулируемые параметры модели Рассчитываемые параметры модели Название Обозначение Пределы Шаг Название Обозначение Пределы Шаг Начальная скорость V0 0–25 м/с 0,1 Время t 0–7 с 0,1 Угол a 0–90 град. 1 Горизонт. координата x 0–100 м 0,1 Высота H 0–60 м 1,0 Верт. координата y 0–100 м 0,1 – – – – Горизонт. скорость Vx 0–25 м.c 0,1 – – – – Верт. скорость Vy 0–42 м.c 0,1

Данную модель можно применять при изучении следующих видов движения: свободное падение тела без начальной скорости, движение тела, брошенного вертикально вверх, движение тела, брошенного горизонтально, движение тела, брошенного под произвольным углом к горизонту (как с поверхности земли, так и с некоторой высоты).

Выяснить характер зависимости дальности полета l от величины начальной скорости v0. Задания: Выбрать определенное значение угла α. Получить экспериментально траектории движения тела при заданном угле α, если значения начальной скорости изменяются с шагом 5 м/с (все траектории получить на одном рисунке). Заполнить таблицу 1. α = ____ V0      l Построить график зависимости l = l (v0). Объяснить характер зависимости l = l (v0) с помощью формулы для нахождения дальности полета l.

Выяснить характер зависимости дальности полета l от угла бросания α. Задания: Выбрать определенное значение начальной скорости v0. С помощью компьютерного эксперимента получить на одном рисунке траектории движения тела при заданном значении начальной скорости v0 в зависимости от угла бросания α. Шаг изменения угла α = 5° ÷ 10°. Заполнить таблицу 2. v0=_____ а    l   Какому значению угла α соответствует максимальная дальность полета? Получить экспериментальные данные и объяснить их. Определить при каких значениях угла α дальность полета одинакова. Почему? Чем отличаются движения тела в данных случаях? При каком значении угла α высота подъема тела наибольшая? Подтвердить формулой.

С помощью компьютерного эксперимента выяснить: Как изменится время и дальность полета тела брошенного горизонтально с некоторой высоты, если начальную скорость бросания увеличить в 2 раза? Как и во сколько раз надо изменить скорость тела, брошенного горизонтально, чтобы при высоте, в 2 раза меньшей, получить прежнюю дальность полета.? Сделать вывод: от чего зависит дальность полета тела, брошенного под углом к горизонту. Подтвердить словесный вывод формулой.

Решим задачу: 209 (192). Стрела, выпущенная из лука вертикально вверх, упала на землю через 6 с. Какова начальная скорость стрелы и максимальная высота подъёма?

Решим задачу: 211 (194). Во сколько раз надо увеличить начальную скорость брошенного вверх тела, чтобы высота подъёма увеличилась в 4 раза?

Решим задачу: 221 (203). Мальчик бросил горизонтально мяч из окна, находящегося на высоте 20 м. Сколько времени летел мяч до земли и с какой скоростью он был брошен, если он упал на расстоянии 6 м от основания дома?

Решим задачу: 222 (204). Как изменится время и дальность полёта тела, брошенного горизонтально с некоторой высоты, если скорость бросания увеличить вдвое?

Решим задачу: 223 (205). Как и во сколько раз надо изменить скорость тела, брошенного горизонтально, чтобы при высоте, вдвое меньшей, получить прежнюю дальность полёта?

Решим задачу: 229. Вратарь, выбивая мяч от ворот (с земли), сообщает ему скорость 20 м/с, направленную под углом 50° к горизонту. Найти время полёта мяча, максимальную высоту поднятия и горизонтальную дальность полёта.

Решим задачу: 234 (214) С балкона, расположенного на высоте 20 м, бросили мяч под углом 30° вверх от горизонта со скоростью 10 м/с. Найти: а) координату мяча через 2 с; б) через какой промежуток времени мяч упадёт на землю; в) горизонтальную дальность полёта.

Примеры заданий проблемного и исследовательского характера

При изучении движения тела, брошенного горизонтально, можно предложить учащимся следующий вопрос: два тела падают с одной и той же высоты, причём первое тело падает без начальной скорости, а второе - с начальной скоростью, направленной горизонтально; какое тело упадёт на землю раньше? Наверняка в классе найдутся ребята, которые считают, что первое тело упадёт раньше. Вот здесь то и пригодится компьютерный эксперимент.

Изучение движения тела, брошенного под углом к горизонту можно начать со следующих вопросов: Как изменится дальность полёта горизонтально брошенного тела при увеличении его начальной скорости в 2 раза? А как изменится дальность полёта тела, брошенного под углом к горизонту, при увеличении его начальной скорости в 2 раза? При каком угле бросания дальность полёта тела максимальна? Этот вопрос можно рассматривать как исследовательское задание.

Компьютерная модель "Упругие и неупругие соударения"

Проведите необходимые компьютерные эксперименты и определите: при каком соотношении масс тележек относительные потери механической энергии при неупругом соударении максимальны. Как должны быть направлены скорости тележек. Задание 1

Задание 2 Проведите необходимые компьютерные эксперименты и определите: при каком соотношении масс тележек относительные потери механической энергии при неупругом соударении минимальны. Рассмотрите следующие случаи: а) одна из тележек до соударения покоится; б) тележки движутся навстречу друг другу; в) одна тележка догоняет другую. Возможно ли, чтобы в результате упругого соударения одна из тележек остановилась. Если да, то при каком условии?

Задание 3 Возможно ли, чтобы в результате упругого соударения одна из тележек остановилась. Если да, то при каком условии?

Как подготовить компьютерную лабораторную работу Выполнение компьютерных лабораторных работ требует определенных навыков, характерных и для реального эксперимента - выбор условий эксперимента, установка параметров опыта и т.д.

Выполнение компьютерных лабораторных работ требует определенных навыков, характерных и для реального эксперимента - выбор условий эксперимента, установка параметров опыта и т.д.

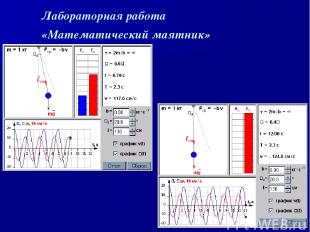
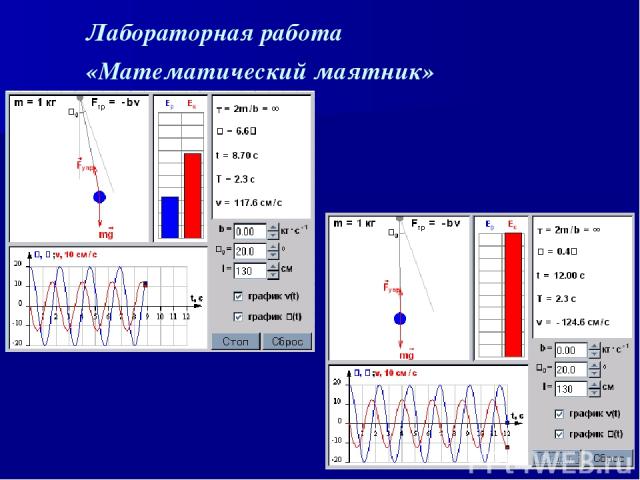
Лабораторная работа «Математический маятник»

Задания к лабораторной работе 1. Математический маятник за 13 с совершил 6,5 полных колебаний. Найти период колебаний. Проведите компьютерный эксперимент и проверьте Ваш ответ. 2. Тело, прикрепленное к нити, совершает гармонические колебания с частотой 0,5 Гц. Определите минимальное время, за которое тело проходит расстояние между положениями, соответствующими максимальным смещениям из положения равновесия. Проведите компьютерный эксперимент и проверьте Ваш ответ.

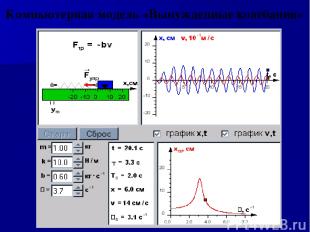
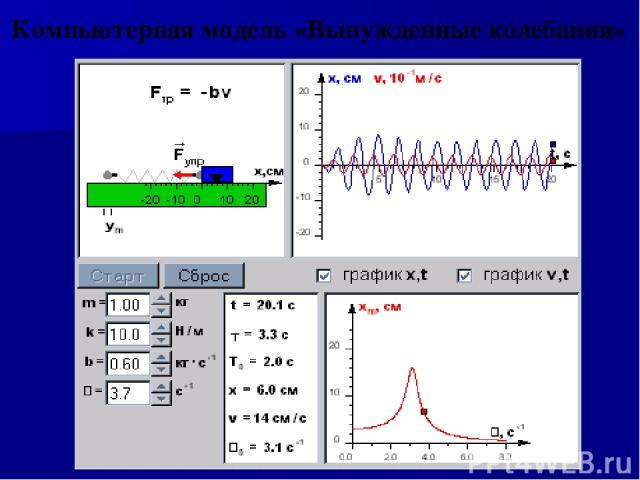
Компьютерная модель «Вынужденные колебания»

Компьютерная модель «Вынужденные колебания» демонстрирует вынужденные колебания груза на пружине. Изменяющаяся по гармоническому закону внешняя сила приложена к свободному концу пружины. В модели можно изменять массу груза m, жесткость пружины k и коэффициент вязкого трения b. Можно одновременно вывести графики зависимости от времени координаты и скорости груза и другие параметры колебаний, рядом расположена резонансная кривая.

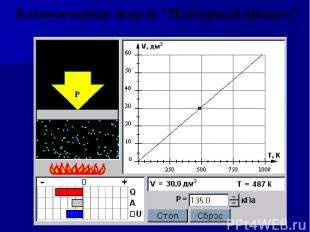
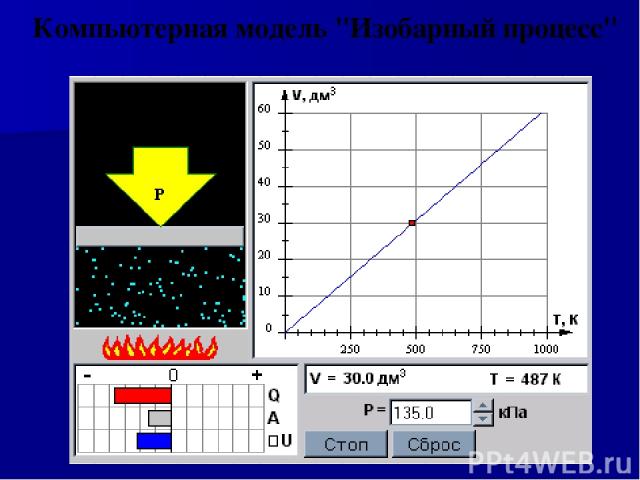
Компьютерная модель "Изобарный процесс"

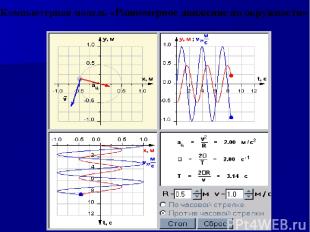
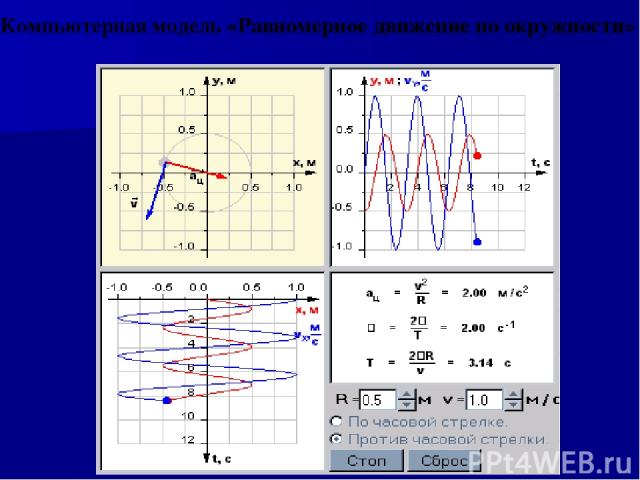
Компьютерная модель «Равномерное движение по окружности»

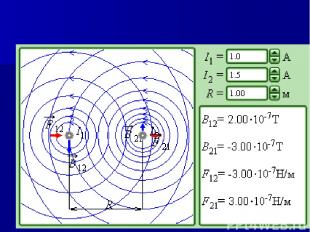
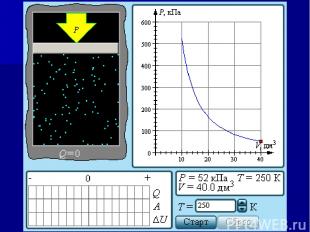
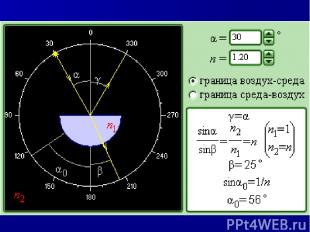
В развитии школьного физического образования на современном этапе играют серьезную роль такие тенденции, как индивидуализация обучения, применение компьютера в обучении. Обучающие компьютерные программы и имитационные программы, моделирующие физические эксперименты: расширяют, углубляют и закрепляют знания о физических явлениях и способах научного познания развивают у школьников исследовательское мышление повышают учебную мотивацию школьников и развивают интерес к физике влияют на профессиональные намерения учащихся