Презентация на тему: Фотоны

Фотоны Лекция 6

§§ Введение 02 1900, гипотеза Планка Излучение и поглощение света веществом происходит не непрерывно, а конечными порциями или квантами Для согласия с классической термодинамикой и электродинамикой: Проблему равновесного излучения с классических позиций решить не удается.

03 при распространении свет ведет себя подобно совокупности частиц (световых квантов – фотонов) 1905, гипотеза Эйнштейна λ = 623 нм (He-Ne лазер) Пример. = 3,19·10–19 Дж ≈ 2 эВ Масса фотона в движении: Энергия фотона: = 3,55·10–36 кг

04 Импульс фотона = 1,06·10–27 кг·м/с При взаимодействии с веществом фотоны могут рассеиваться, испускаться и поглощаться. Число фотонов не сохраняется, зато должны выполняться законы сохранения импульса и энергии.

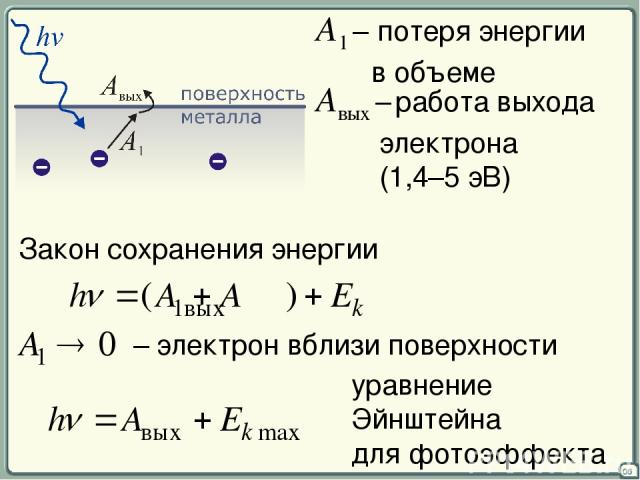
§§ Внешний фотоэффект 05 Фотоэффект – испускание электронов веществом под действием света. 1905, А.Эйнштейн Пусть поверхность металла освещается монохроматическим светом с частотой ν Электрон не может «поглотить» фотон из-за закона сохранения МИ (спина).

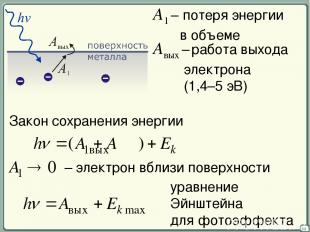
06 A1 – потеря энергии в объеме Aвых – работа выхода электрона (1,4–5 эВ) Закон сохранения энергии уравнение Эйнштейна для фотоэффекта

07 Существование красной границы: Металл λmax, нм Cs 686 K 560 Na 540 Li 521 Hg 273,5 Fe 262 Ag 261 Au 265 п/п λmax, нм Ge 260 Si 258 УФ Работа выхода, эВ Cs 1,81 K,Na,Li 2,22–2,38 Hg…Au 4,55–4,75

08 Для прекращения эмиссии электронов необходимо приложить задерживающую разность потенциалов Приложение ускоряющей разности потенциалов используется в фотоэлектронном умножителе Ускоренные электроны могут вызвать и свечение люминофора (приборы ночного видения, тепловизоры) KУ~106–108

Применение 09 1) Приёмники и усилители сигналов ЭМВ в электрические сигналы (R, U, I) 2) Преобразователи ЭМВ ИК и УФ в излучение видимого диапазона

10 Наблюдение объекта через тепловизор позволяет выявить утечки, слабые места, избежать аварии.

§§ Внутренний фотоэффект 11 В диэлектриках и полупроводниках электрон изменяет свою энергию не выходя на поверхность. У вещества изменяется проводимость (фоторезисторы). В неоднородных полупроводниках также наблюдается фотогальванический эффект – образование разности потенциалов под действием света.

Фотоэлементы (солнечные батареи) в настоящее время используют как источники электроэнергии 1) основа – кремний (Si) 2) КПД от 10 до 20% 3) Фото-ЭДС: 1–2 В 4) Фототок: ~0,01 А с площади в 1 см2 (сотни ватт с 1 м2) 12

13 Фотоэффект применяют в науке (измерения) в технике: усилители и преобразователи организация электропитания связь контроль и управление

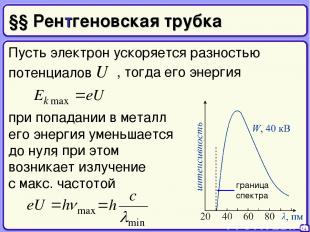
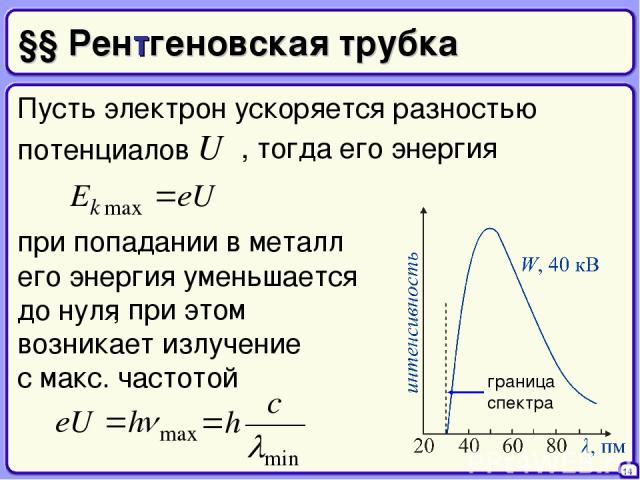
§§ Рентгеновская трубка Пусть электрон ускоряется разностью потенциалов U 14 , тогда его энергия при попадании в металл его энергия уменьшается до нуля , при этом возникает излучение с макс. частотой

§§ Эффект Комптона 15 1922–23 г., Артур Комптон исследовал рассеяние рентгеновского излучения на телах, состоящих из легких атомов (графит, парафин). Оказалось, что в рассеянном излучении содержится две линии: λ и λ+Δλ и не зависит от состава тела и длины волны λ Смещение

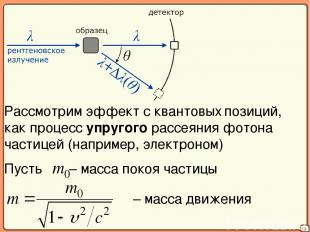
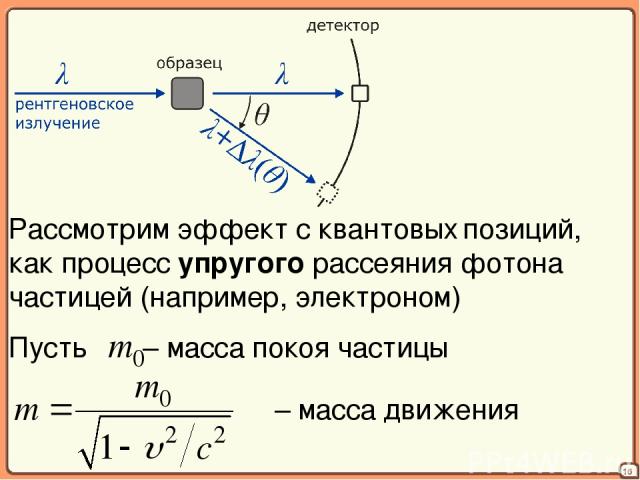
16 Рассмотрим эффект с квантовых позиций, как процесс упругого рассеяния фотона частицей (например, электроном)

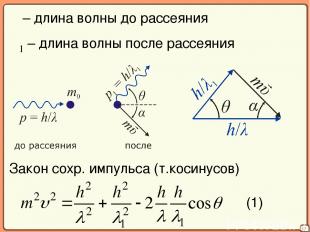
17 λ – длина волны до рассеяния λ1 – длина волны после рассеяния Закон сохр. импульса (т.косинусов) (1)

18 Закон сохранения энергии (2) Возведем в квадрат:

19 Вычтем: (1)–(2)

20 Если рассеяние происходит на электроне – комптоновская длина волны электрона Рассеяние происходит на случайный угол. Если электрон не оторвется от атома, то смещения по длине волны не будет. Иногда наблюдается и обратный эффект Комптона – уменьшение длины волны у рассеянного излучения.

§§ Гипотеза Де Бройля 21 В оптических явлениях наблюдается дуализм. 1924, Луи Де Бройль (Louis De Broglie) гипотеза о всеобщем характере корпускулярно-волнового дуализма Это универсальное свойство природы – всем микрообъектам присущи одновременно и корпускулярные и волновые свойства

Если двигается частица массой m со скоростью υ 22 Энергия фотона: Импульс фотона: , то с частицей можно ассоциировать волну с длиной – длина волны Де Бройля Пример: электрон, ускоренный разностью потенциалов в 12 кВ E = 12 кэВ = 1,92·10–15 Дж λ = 10–10 м

23 Дифракция микрочастиц (электронов, атомов и молекул) наблюдается аналогично дифракции рентгеновского излучения Для того, чтобы интерпретировать явления интерференции и дифракции микрочастиц принимают, что Интенсивность сопоставляемой волны пропорциональна вероятности обнаружения частицы в этой точке

Соотношение неопределённостей 24 В классической механике у каждой частицы были свои координаты и импульс в каждый момент времени. следует принцип неопределенности Из формулы де Бройля

25 Пусть импульс частицы p нам известен точно (Δp = 0) , тогда волна, ассоциированная с частицей – строго монохроматическая Это бесконечная sin волна, занимающая все пространство (Δx = ∞) Пусть частица локализована в области пространства Δx = L. Тогда ей соответствует волновой пакет (набор волн, импульсов), т.е. Δp ≠ 0

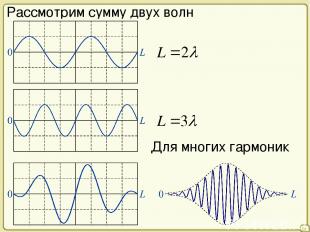
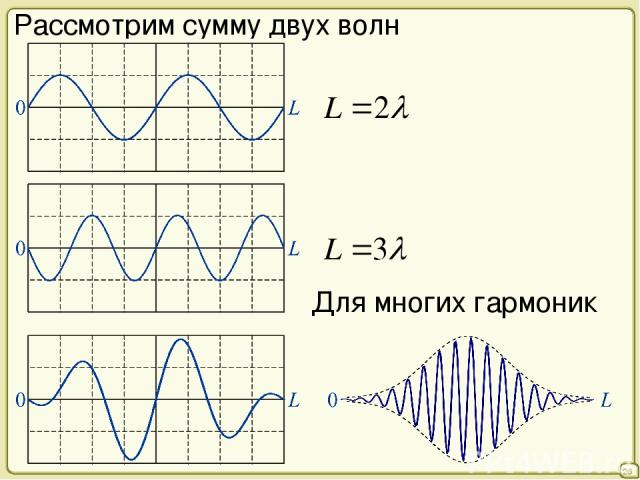
26 Рассмотрим сумму двух волн Для многих гармоник

27 Пусть и тогда или

28 Более строгое выражение называется соотношением неопределенностей Гейзенберга Это означает, что в квантовой механике нет (не применимо) понятие траектории частицы Можно говорить лишь о вероятности нахождения частицы в данной области пространства.

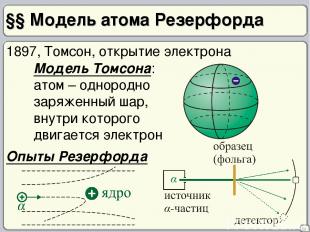
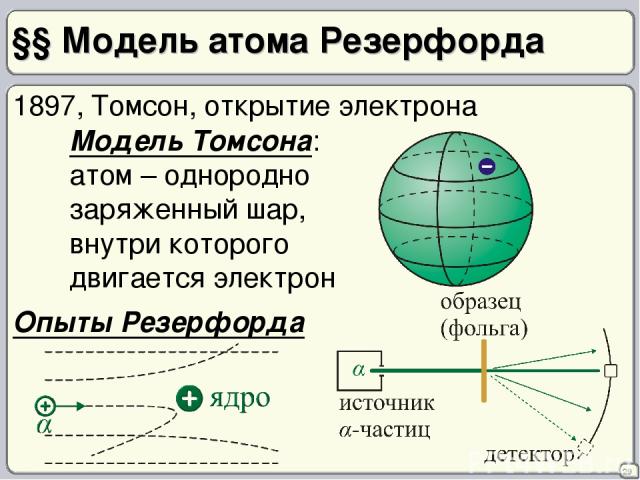
§§ Модель атома Резерфорда 29 1897, Томсон, открытие электрона Модель Томсона: атом – однородно заряженный шар, внутри которого двигается электрон Опыты Резерфорда

30 Ядерная модель атома 1) Атом – система зарядов, в центре которой располагается тяжелое положительно заряженное ядро Q = Z|e| dя ~ 10–14 – 10–15 м 2) вокруг ядра – Z электронов dA ~ 10–10 м (несколько Å) Трудности: 1) Система зарядов либо непрерывно излучает энергию, либо неустойчива 3) Тождественность атомов 2) Линейчатый спектр

§§ Теория Бора 31 Пусть электрон двигается по круговой орбите С электроном свяжем волну Де Бройля:

32 Пусть на длине окружности укладывается целое число длин волн (условие max): т.е. момент импульса электрона на орбите принимает только дискретные значения (т.е. «квантуется»): n = 1,2,3...– главное квантовое число

33 Заряд ядра атома: Z – порядковый номер элемента e = –1,6·10–19 Кл – заряд электрона Сила, действующая на электрон , k = 9·10–9 Н·м/Кл2 по II-му закону Ньютона

34 Получаем систему ее решение – скорость электрона – радиус орбиты

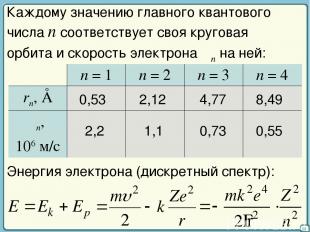
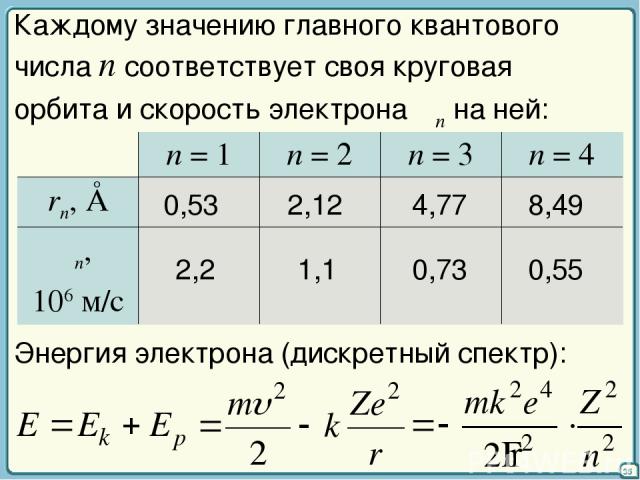
35 Каждому значению главного квантового числа n соответствует своя круговая орбита и скорость электрона υn на ней: 0,53 2,12 4,77 8,49 2,2 1,1 0,73 0,55 Энергия электрона (дискретный спектр): n = 1 n = 2 n = 3 n = 4 rn, Å υn, 106 м/с

36 При переходе атома (Z = 1) из состояния с главным квантовым числом n в состояние с m испускается или поглощается квант с энергией: 13,54 эВ = 2,2·10–18 Дж , R = 2,06·1016 рад/с

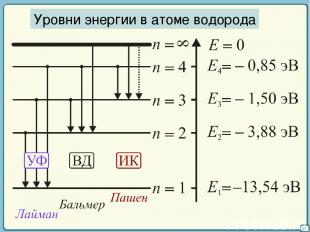
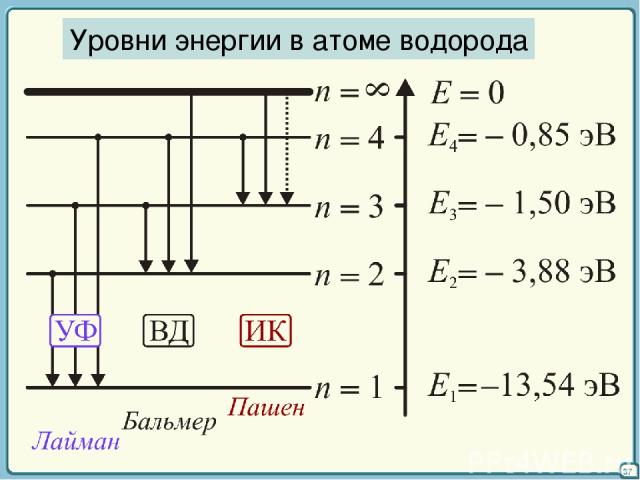
37 Уровни энергии в атоме водорода

37 Теория Бора для атома водорода (а также He+, Li++, Be+++, …) позволила объяснить сложное строение спектра излучения с высокой точностью. Уточнение теории – учет поправок, связанных с движением электрона и ядра относительно общего центра масс. Недостатки: 1) она не квантовая и не классическая 2) нельзя построить теорию атома гелия