Презентация на тему: Интерференция света

Лекция №2

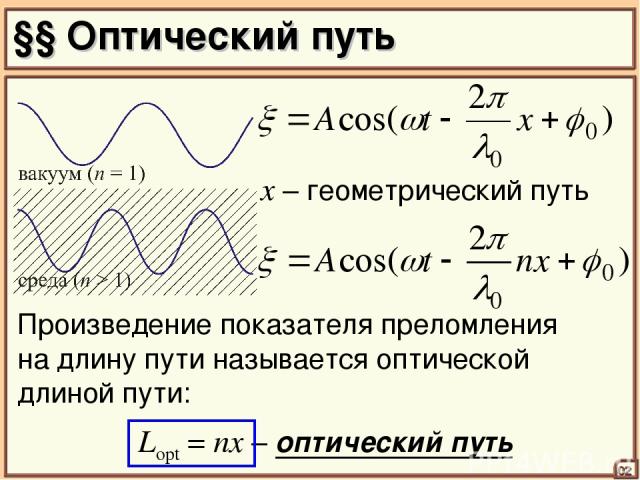
§§ Оптический путь 02 x – геометрический путь Lopt = nx – оптический путь Произведение показателя преломления на длину пути называется оптической длиной пути:

Пример 1: прохождение света через прозрачную пластинку 03 Пример 2: Оптическая разность хода двух волн Если первая волна прошла путь L1 в среде с n1, а вторая – путь L2 в среде с n2 то и

Пример 3: Отражение от границы раздела двух сред 04 т.е. возникает дополнительный набег фазы при отражении от оптически более плотной среды

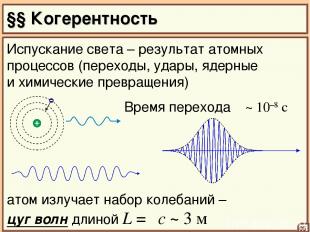
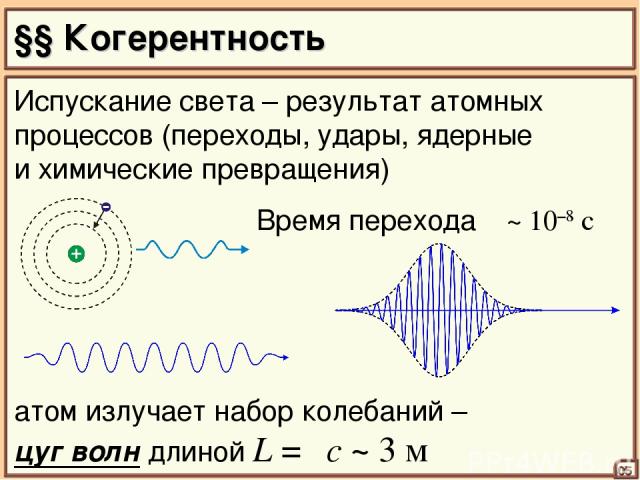
§§ Когерентность 05 Испускание света – результат атомных процессов (переходы, удары, ядерные и химические превращения) Время перехода τ ~ 10–8 c атом излучает набор колебаний – цуг волн длиной L = τc ~ 3 м

06 Излучение отдельного атома – немонохроматично, а излучение разных атомов – некогерентно. Свет от источника состоит из быстро сменяющих друг друга цугов со случайным значением начальной фазы. Если в одну точку приходит свет от разных источников (или частей одного тела), то результат различается в каждый момент времени.

07 Устойчивая интерференционная картина наблюдается только для когерентных (согласованных) колебаний. Временем когерентности называют промежуток времени, в течение которого случайное изменение фазы (или разности фаз) достигает π. Если время разрешения прибора больше времени когерентности или разность хода больше длины когерентности, то регистрируются значения согласно закону сложения интенсивностей.

08 Для получения двух потоков когерентного излучения необходимо использовать излучение одного атома Для этого, с помощью отражения или преломления, нужно разделить волну и позволить потокам, прошедшим разное расстояние, встретиться. Разность пройденных расстояний не должна превышать длины цуга или длины когерентности. или группы атомов, излучающих согласованно.

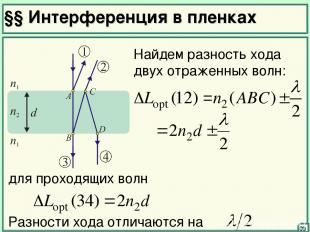
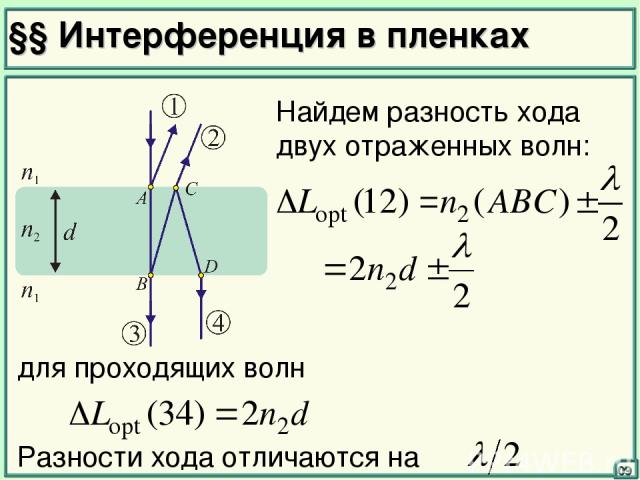
§§ Интерференция в пленках 09 Найдем разность хода двух отраженных волн: для проходящих волн Разности хода отличаются на

10 Следовательно, максимум на отражение соответствует минимуму на пропускание Максимум при пропускании будет наблюдаться, если и соответствующая толщина пленки:

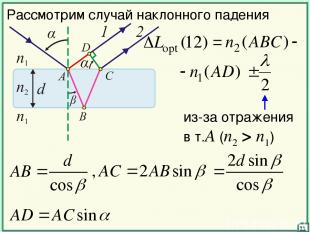
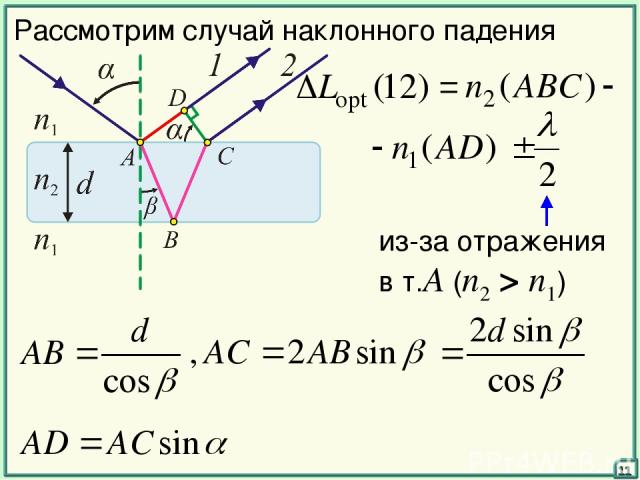
11 Рассмотрим случай наклонного падения из-за отражения в т.А (n2 > n1)

12 При падении белого света будут наблю-даться min и max под разными углами, которые соответствуют различным λ

§§ Кольца Ньютона 13 наблюдаются в месте контакта линзы и, например, стеклянной пластины

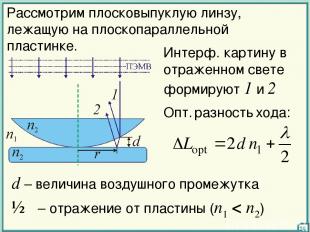
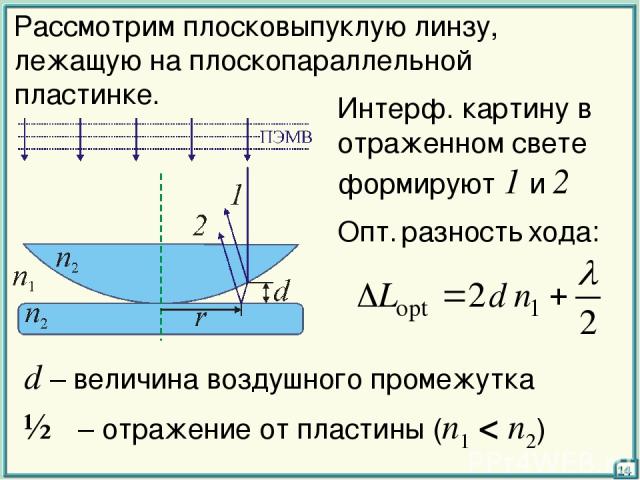
Рассмотрим плосковыпуклую линзу, лежащую на плоскопараллельной пластинке. 14 Интерф. картину в отраженном свете формируют 1 и 2 Опт. разность хода: d – величина воздушного промежутка ½λ – отражение от пластины (n1 < n2)

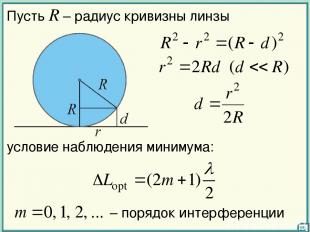
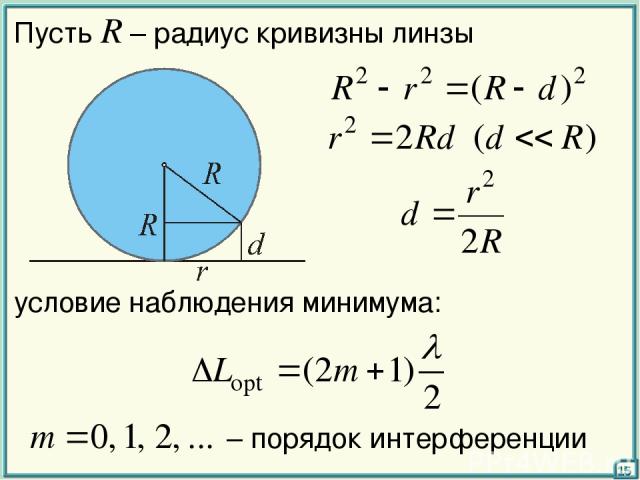
Пусть R – радиус кривизны линзы 15 условие наблюдения минимума:

16 – радиус m-го темного кольца Ньютона – радиус m-го светлого кольца

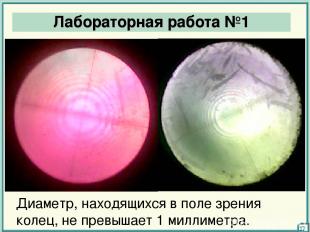
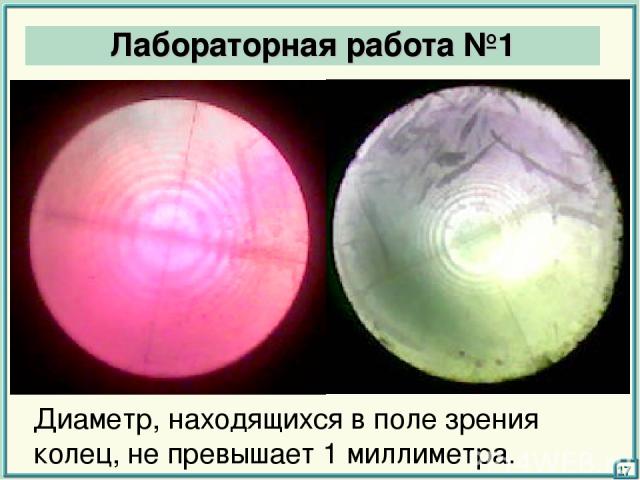
Лабораторная работа №1 17 Диаметр, находящихся в поле зрения колец, не превышает 1 миллиметра.

Замечания Кольца Ньютона – классический пример полос равной толщины. 18 Кольца можно наблюдать в отраженном и проходящем свете. При падении белого света – получается система цветных колец.

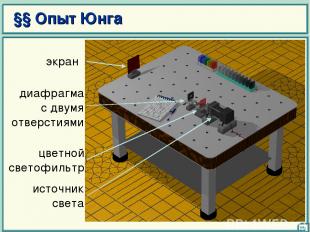
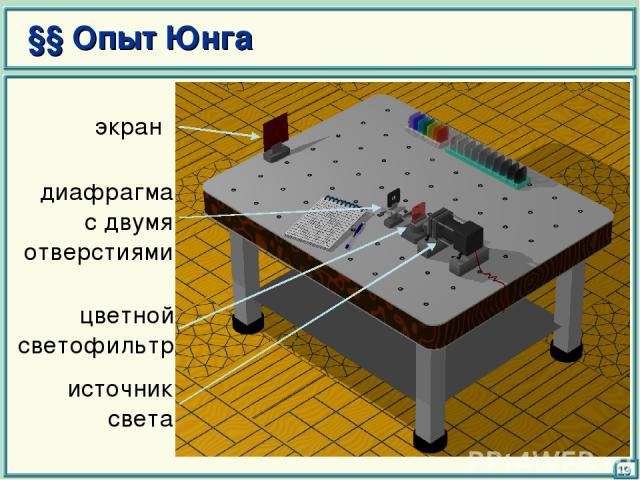
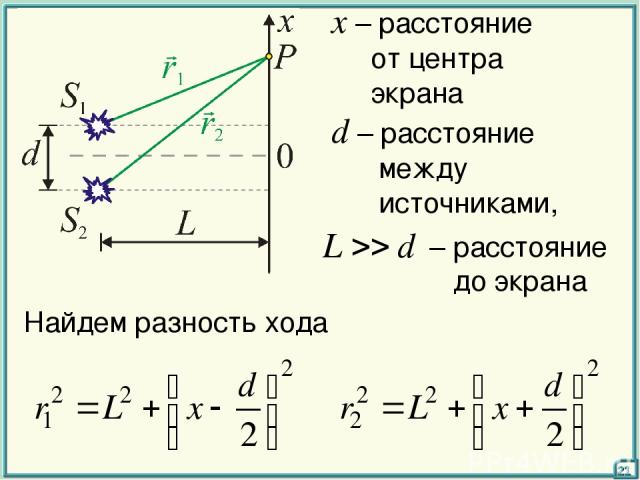
§§ Опыт Юнга 19

на экране наблюдается интерференционная картина – совокупность светлых и темных областей (полос) определим положения min и max интенсивности 20

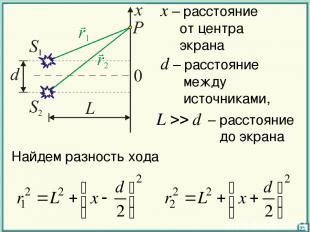
d – расстояние между источниками, x – расстояние от центра экрана Найдем разность хода 21

вычтем одно выражение из другого: левую часть можно представить как тогда разность хода двух лучей: Условие наблюдения минимума: 22

– координата m-го минимума – координаты максимумов Ширина полосы (период интерференционной картины) – расстояние между соседними минимумами (максимумами): 23

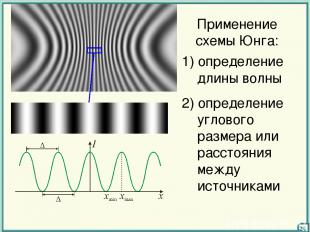
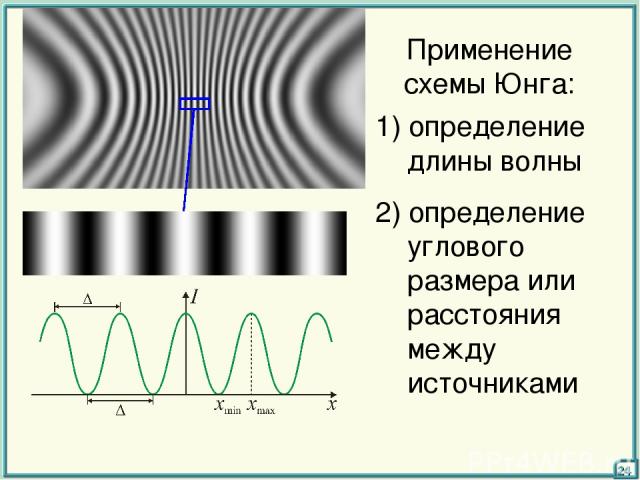
Применение схемы Юнга: 1) определение длины волны 2) определение углового размера или расстояния между источниками 24

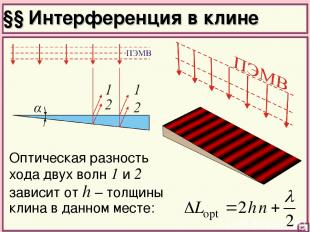
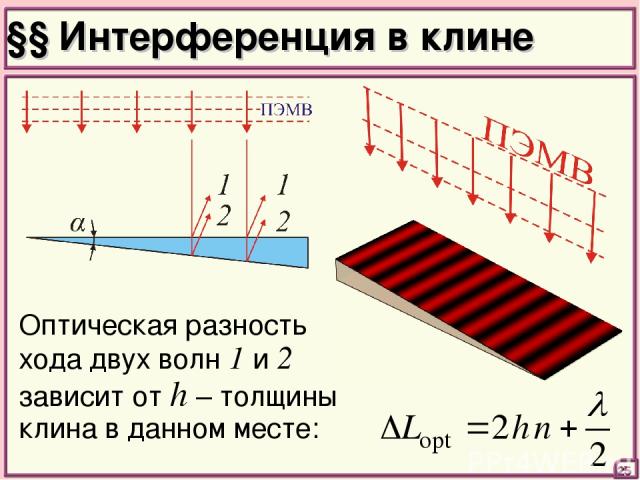
§§ Интерференция в клине Оптическая разность хода двух волн 1 и 2 зависит от h – толщины клина в данном месте: 25

26 условие наблюдения максимума: и зависимость толщины клина h от расстояния x до его кромки: светлые полосы наблюдаются при значениях xm: наблюдаются полосы равной толщины

27 Расстояние между соседними полосами: Рассмотренная схема позволяет: определять длину волны света λ, показатель преломления среды n или угол раствора клина α с очень малой погрешностью.

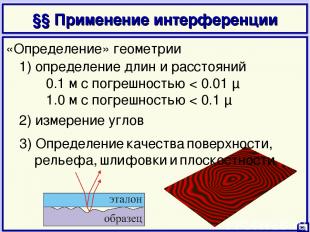
§§ Применение интерференции 28 1) определение длин и расстояний 0.1 м с погрешностью < 0.01 μ 1.0 м с погрешностью < 0.1 μ 2) измерение углов «Определение» геометрии 3) Определение качества поверхности, рельефа, шлифовки и плоскостности

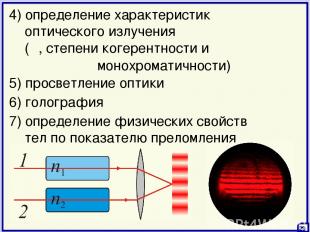
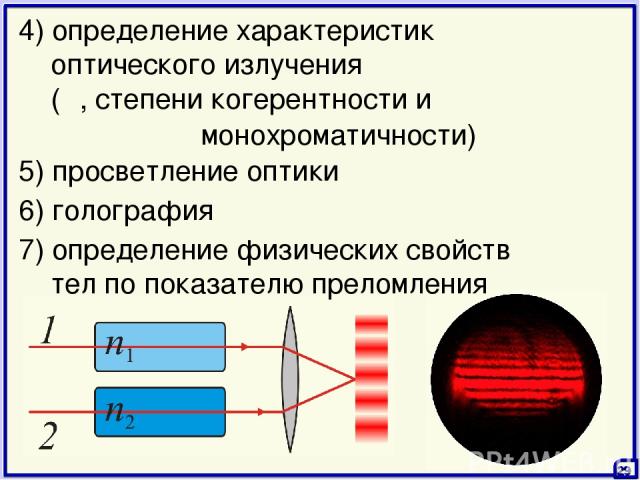
(λ, степени когерентности и монохроматичности) 5) просветление оптики 4) определение характеристик оптического излучения 29 7) определение физических свойств тел по показателю преломления 6) голография

30 Другие случаи:

§§ Показатель преломления Из теории Максвелла следует, что – показатель преломления 31 Длина волны света в среде:

32 ЭМВ, распространяясь в веществе, вызывает вынужденные колебания ионов решетки и электронов. Этим объясняется явление дисперсии – зависимость скорости ЭМВ от частоты, поскольку ε и, следовательно, n зависят от частоты ЭМВ. Колебаниями электронов объясняется дисперсия в видимой области, а колебаниями ионов – в инфракрасной, т.к. их масса значительно больше.

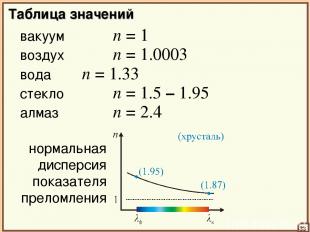
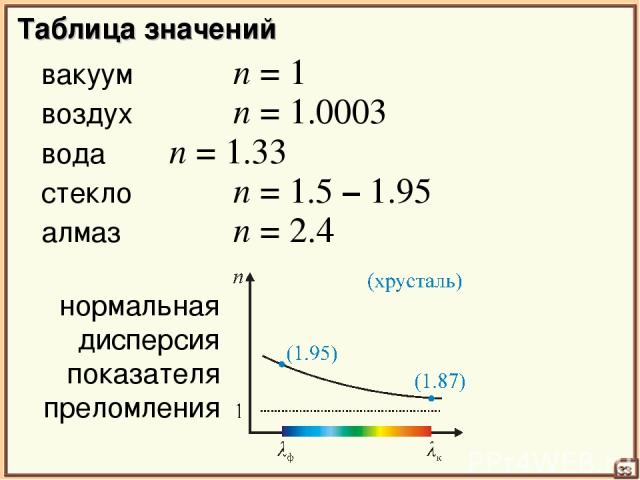
Таблица значений вакуум n = 1 33 воздух n = 1.0003 вода n = 1.33 стекло n = 1.5 – 1.95 алмаз n = 2.4 нормальная дисперсия показателя преломления

34