Презентация на тему: Физика «Мощность, энергия, работа»

РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ Сегодня: * 900igr.net

Лекция Тема: РАБОТА, МОЩНОСТЬ, ЭНЕРГИЯ. ЗАКОНЫ СОХРАНЕНИЯ Введение Содержание лекции: Сегодня: * 1. Работа 2. Мощность 3. Кинетическая энергия тела 4. Потенциальная энергия 5. Консервативные силы 6. Закон сохранения полной механической энергии 7. Удар шаров 8. Энергия в биологии

Введение Существует экспериментальный факт: вечное движение механических устройств и машин невозможно. Недопустимость вечного движения говорит о том, что есть некая физическая величина, сохраняющаяся со временем. Эта величина в физике получила название энергии. Энергия общая количественная мера движения и взаимодействия всех видов материи.

Энергия не возникает из ничего и не исчезает, она может переходить из одной формы в другую- закон сохранения энергии. Этот закон налагает строгие ограничения на возможности преобразования и использования энергии.

Закон сохранения энергии связан с однородностью времени, т.е. с тем фактом, что все моменты времени эквивалентны и физические законы не меняются со временем. Закон сохранения энергии для механических процессов установлен Лейбницем в 1686 г., для немеханических явлений Майером в 1845 г., Джоулем в 1843 и Гельмгольцем в 1847.

5.2. Работа Сила, действующая на движущееся тело, совершает над ним работу. Количественно совершаемая силой работа равна произведению составляющей силы в направлении движения на пройденное расстояние Например, на рис. 1 человек перемещает санки с детьми на расстояние r, прилагая к веревке постоянную силу F. Работа, которую производит человек над санками, равна A = Frr.

Рис. 1 F a r Работа равна произведению Frr, а не F, где Fr – составляющая полной силы F в направлении r. Поскольку Fr= Fcos , приведенное выше выражение можно записать в виде A = Frcos .

Работа равна скалярному произведению A = (F,r). Если сила не постоянна, то работа на бесконечно малом отрезке пути dr запишется в виде dA = (F,dr).

Полная работа, производимая при перемещении тела из точки C в точку D, равна

В механике работа служит мерой передачи движения от одного тела к другому, или мерой перехода энергии от одного тела к другому. Когда сила действует на движущееся тело и направление силы и скорости движения совпадают, то работу силы считают положительной. Если же направление силы и перемещение тела противоположны, то работа силы считается отрицательной.

Работа и энергия измеряются в СИ в единицах произведения силы на расстояние, т.е. в ньютонах на метр (Н м); размерность этой величины МL2T–2. Эта единица нашла довольно широкое употребление и называется джоулем (Дж).

В атомной и ядерной физике в качестве единицы измерения энергии широко используется электроновольт (эВ): 1 эВ = 1,6 10 19 Дж.

Пример 1. Допустим, что на рис.1 угол = 30 и человек идет с постоянной скоростью 1,5 м/с и производит ежесекундно работу 100 Дж. Найдем силу F, с которой человек тянет веревку. Поскольку ежесекундно преодолевается путь r = 1,5 м, из определения работы получаем F r cos = A; Работа совершается со скоростью, соответствующей ежесекундному поднятию тела массой 10 кг на высоту около 1 м. Это, безусловно, тяжелая работа.

Пример 2. Определим работу, необходимую для того, чтобы растянуть пружину на длину х. Подставим в выражение A = (F,dr) вместо силы F величину kx (линейная зависимость силы от х называется законом Гука) и заменим dr на dx. Таким образом, При интегрировании мы использовали табличный интеграл

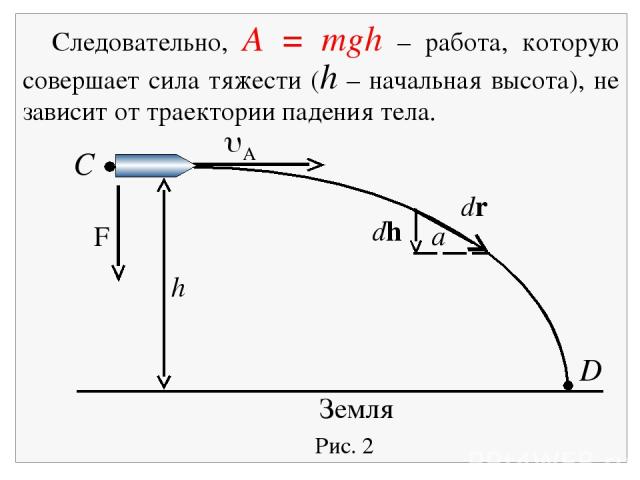
Пример 3. Определим работу, совершаемую силой тяжести при падении снаряда массой m с высоты h, летящего со скоростью v. Для этого вычислим интеграл в случае, когда угол между векторами непрерывно меняется. Заметим, что элементарная работа дается выражением Fdr = mg(drcos ). Из рис. 5.3 имеем (drcos ) = dy. Совершив эту подстановку и вычислив интеграл, получим

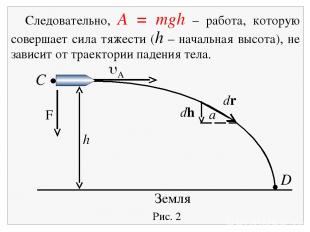
Рис. 2 Земля F С D a dr dh uA h Следовательно, A = mgh – работа, которую совершает сила тяжести (h – начальная высота), не зависит от траектории падения тела.

5.3. Мощность Скорость совершения работы (передачи энергии) называется мощностью и обозначается W. Согласно определению можем записать W dA/dt. Величина W характеризует мгновенное значение скорости передачи энергии. В СИ единицей измерения мощности является джоуль в секунду (Дж/с).

Эта единица имеет размерность ML2T–3 и называется ваттом (Вт). Электрическая лампочка мощностью100 Вт расходует 100 Дж/с. Произведение мощности на время дает энергию. Широко используется единица энергии киловатт час (к Вт ч): 1 кВт ч = 103 Вт 3600 с = 3,6 106 Дж. В России ежедневно потребляется в среднем 1,3 1013 кВт ч энергии.

Понятие мощности является одной из важнейших характеристик различных машин и механизмов. Мощность показывает, насколько быстро могут совершить одну и ту же работу различные механические устройства. Так, экскаватор способен выкопать котлован под фундамент дома за сутки. Человек на ту же работу будет вынужден затратить год.

Двигатели автомобиля, катера, самолета должны обладать большой мощностью, чтобы они могли преодолевать действующую силу сопротивления движению, когда движение происходит с большой скоростью W = (F,v) - скалярное произведение

5.4. Кинетическая энергия тела Движущееся тело представляет собой самую простейшую форму движения материи. Мерой величины этого движения является кинетическая энергия. Величину кинетической энергии тела можно определить по величине работы, которую необходимо совершить, чтобы вызвать данное движение тела.

Пусть сила F действует на тело массой m и вызывает его движение из точки С в точку D. В точке С тело покоилось, в точке D тело имеет скорость v. Работа силы F на пути CD пошла на увеличение кинетической энергии тела. Эта работа записывается в виде

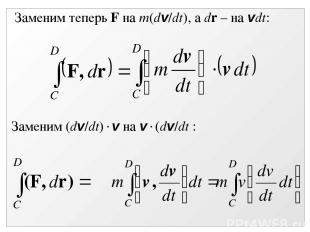
Заменим теперь F на m(dv/dt), а dr – на vdt: Заменим (dv/dt) v на v (dv/dt :

Таким образом, Окончательно получаем: Совершаемая работа силой при перемещении тела из точки С в точку D равна разности кинетических энергий в этих точках.

Кинетическая энергия тела массой m, движущегося со скоростью v, равна K = mv2/2. Размерность кинетической энергии K совпадает с размерностью работы (Дж). Использование понятия энергии при решении многих задач механики является наиболее рациональным. В этом случае отпадает необходимость прослеживать траектории движения частиц, детали взаимодействия тел, обмена энергией и импульсом.

Определим скорость снаряда на рис. 2 в момент, когда он падает на Землю в точке D. Сила F = mg направлена к центру Земли. Поэтому интеграл равен mgh. Подставляя в левую часть соотношения эту величину, получаем

Пусть 30-метровый водопад расходует m = 10 кг воды в секунду. Найдем количество выделяющейся ежесекундно энергии. Согласно соотношению K = mgh, поток падающей воды ежесекундно приобретает кинетическую энергию K = (10 кг)(9,8 м/с2)(30 м) = 2,9 кДж. Если эти 2,9 кДж/с преобразовать в электричество с КПД 100%, то мы могли бы получить 2,9 кВт электроэнергии.

Из последнего примера следует, что приличный водопад мог бы обеспечить 2 или 3 кВт мощности для домашних нужд. Однако в типичном доме потребляется не 2–3, а 10–20 кВт Потребности общества в энергии растут столь сильно, что обычные источники на Земле уже не могут их обеспечить. Большая часть ГЭС работает с полной отдачей; между тем они удовлетворяют потребности в энергии лишь на 4%.

5.5. Потенциальная энергия Для многих видов сил, называемых консервативными, интеграл не зависит от пути интегрирования между точками C и D, а определяется только начальным и конечным положением точек C и D.

Рис. 3 По определению если F – консервативная сила, то (рис. 3) Путь 1 Путь 2 Путь 3

Работа, совершаемая консервативной силой, не зависит от пути, по которому тело перемещается из произвольной точки А в точку В. Математически эквивалентно следующее утверждение: в поле консервативных сил интеграл (F,dr), вычисленный по любому замкнутому пути, равен нулю. Следовательно, в случае консервативных сил нельзя непрерывно приобретать (или терять) энергию, повторяя один и тот же замкнутый путь.

Для обладающих таким свойством сил, интеграл называют потенциальной энергией и обозначают буквой U: Потенциальную энергию можно представить себе как энергию, запасенную для дальнейшего использования. Во многих случаях при желании ее можно преобразовать в другие полезные формы энергии.

Все четыре типа фундаментальных сил, действующих между элементарными частицами, консервативные. Примером неконсервативной силы является трение. В этом случае F и dr всегда направлены в противоположные стороны и интеграл (F,dr) по замкнутому пути всегда отрицателен (тело непрерывно теряет энергию).

Определим потенциальную энергию массы m на расстоянии h над поверхностью Земли. Согласно закону всемирного тяготения Ньютона F = – mg (Знак минус указывает направление силы.) По определению U= – (F, dr) = mgh

5.6. Закон сохранения полной механической энергии Закон сохранения энергии – один из центральных Закон физики и техники. Этот закон налагает строгие ограничения на возможности извлечения энергии и ее преобразования из одной формы в другую. Закон сохранения энергии запрещает существование вечных двигателей.

Согласно этому закону, сумма кинетической и потенциальной энергий всех тел в любой замкнутой консервативной системе остается постоянной. Под замкнутой мы понимаем систему, в которой отсутствуют любые внешние силы. Консервативность означает, что все силы взаимодействия в системе консервативны.

Закон сохранения энергии для системы n материальных точек в поле консервативных сил Из закона изменения импульса F=dP/dt (закон Ньютона) вытекает следующий важный закон, называемый законом сохранения импульса: Импульс замкнутой системы не изменяется с течением времени dP/dt=0; P= const

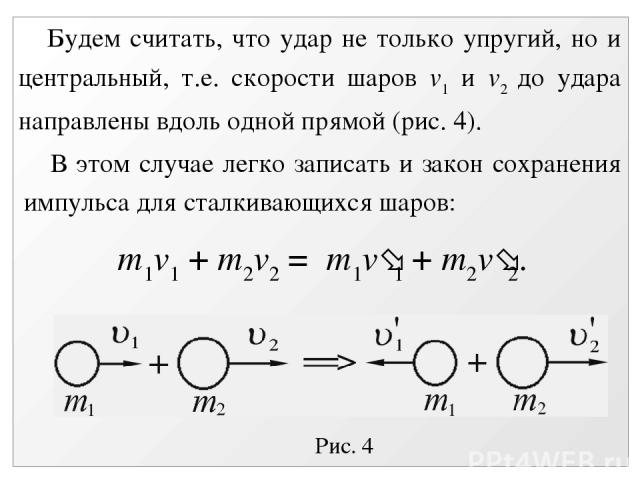
5.7. Удар шаров Удар шаров рассматривается в двух приближениях – абсолютно упругий удар и абсолютно неупругий. При абсолютно упругом ударе не происходит потерь кинетической энергии, связанной с движением шаров Здесь m1, m2 – массы сталкивающихся шаров, v1, v2 – их скорости до удара, v 1, v 2 – скорости шаров после удара.

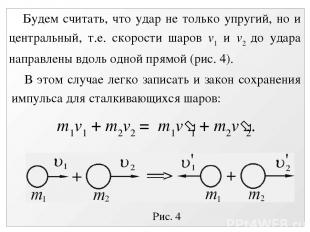
Рис. 4 Будем считать, что удар не только упругий, но и центральный, т.е. скорости шаров v1 и v2 до удара направлены вдоль одной прямой (рис. 4). В этом случае легко записать и закон сохранения импульса для сталкивающихся шаров: m1v1 + m2v2 = m1v 1 + m2v 2.

Полученные два уравнения позволяют найти две неизвестные скорости шаров v 1 и v 2 после удара. Для этого перепишем первое и второе уравнения в виде m1[v12 (v 1)2] = m2[(v 2)2 v22], m1[v1 v 1] = m2[v 2 v2]. Разделив первое уравнение на второе при условии, что скорости шаров изменяются при ударе, находим v1 + v 1 = v2 + v 2

Полученное уравнение, наряду с законом сохранения импульса, составляют систему двух линейных уравнений: m1v1 + m2v2 = m1v 1 + m2v 2. v1 + v 1 = v2 + v 2. Решив систему, получаем

Если второй шар был до удара неподвижен (v2 = 0), то получаем При m1 > m2 первый шар будет двигаться в первоначальном направлении, при m1 < m2 шар отскочит в противоположном направлении, при m1 = m2 первый шар остановится, а второй будет двигаться вперед со скоростью v 2 = v1 – первого шара до удара.

И, в общем случае, при столкновении двух одинаковых шаров (m1 = m2) v 1 = v2, v 2 = v1 шары просто обмениваются скоростями.

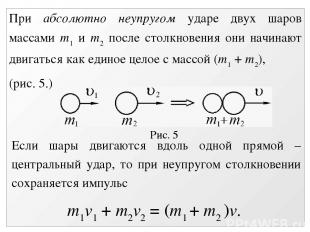
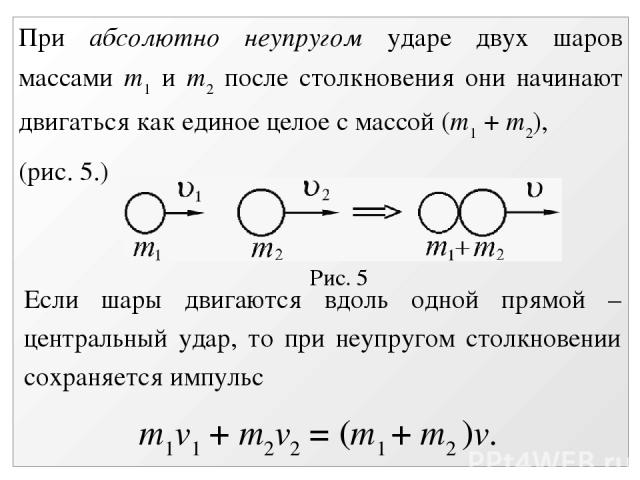
Рис. 5 При абсолютно неупругом ударе двух шаров массами m1 и m2 после столкновения они начинают двигаться как единое целое с массой (m1 + m2), (рис. 5.) Если шары двигаются вдоль одной прямой – центральный удар, то при неупругом столкновении сохраняется импульс m1v1 + m2v2 = (m1 + m2 )v.

Скорость движения после неупругого удара равна Потеря кинетической энергии в системе при неупругом ударе равна разности кинетических энергий до и после удара:

За счет потери кинетической энергии происходит увеличение внутренней энергии системы сталкивающихся шаров, сопровождающееся разрушением тел при столкновении и их нагревом.

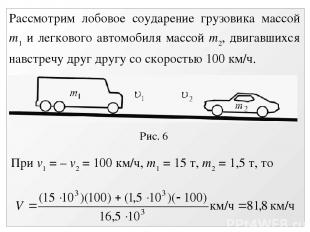
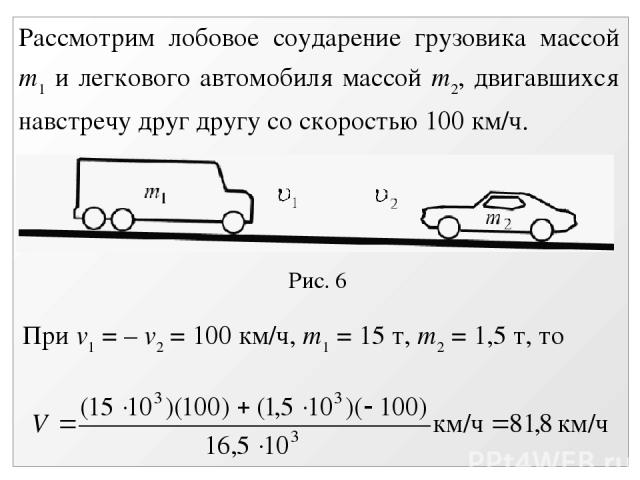
Рис. 6 Рассмотрим лобовое соударение грузовика массой m1 и легкового автомобиля массой m2, двигавшихся навстречу друг другу со скоростью 100 км/ч. При v1 = – v2 = 100 км/ч, m1 = 15 т, m2 = 1,5 т, то

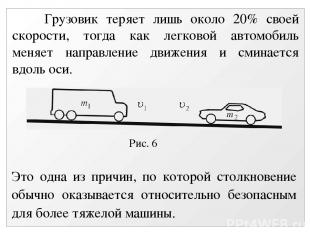
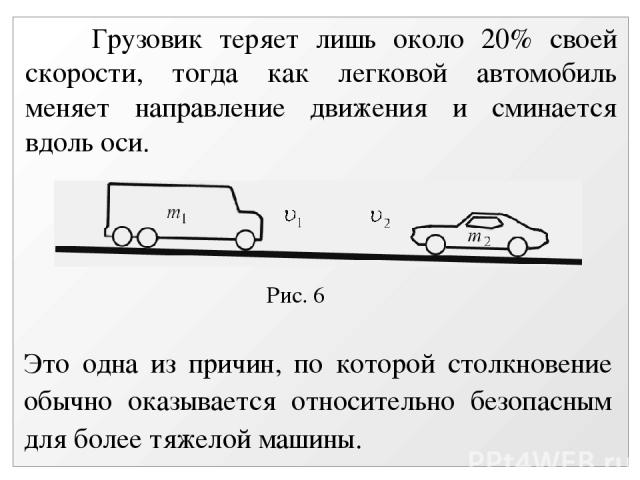
Рис. 6 Грузовик теряет лишь около 20% своей скорости, тогда как легковой автомобиль меняет направление движения и сминается вдоль оси. Это одна из причин, по которой столкновение обычно оказывается относительно безопасным для более тяжелой машины.

5.8. Энергия в биологии Химическая энергия – одна из форм потенциальной энергии. В процессе образования молекул межатомные силы притяжения совершают работу и высвобождается энергия в виде тепла. В живых организмах источниками химической энергии служат углеводы (соединений углерода с водородом). Соединяясь с кислородом, углеводы образуют Н2О и СО2 с высвобождением энергии. Количество высвобождающейся энергии составляет 20000 Дж на 1 г углеводов. Почти вдвое больше химической энергии на 1 г запасено в жире животных.

При сжигании углеводного «топлива» в клетках мышц около 25% энергии переходит в механическую работу. У лошади «топливо» сгорает со скоростью 2000 Вт. Это позволяет ей совершать механическую работу с мощностью 500 Вт. В течение более коротких промежутков времени лошадь способна вырабатывать 700 800 Вт мощности. Эти данные и привели к «лошадиной силе», равной мощности 746 Вт.

Организм человека слабее и в лучшем случае может совершать в единицу времени механическую работу около 100 Вт. Даже во время сна лишь для поддержания нормальных функций организма у взрослого человека «топливо» сгорает со скоростью 80 Вт. Эта величина называется основной скоростью обмена веществ. Такую же мощность потребляет электрическая лампочка средней величины.

В бодрствующем состоянии, например на лекции по физике, студент расходует около 150 Вт, в том числе: 80 Вт плюс около 40 Вт затрачиваются на работу мозга и 15 Вт на работу сердца. При умеренных физических нагрузках, например, во время езды на велосипеде или во время плавания человек затрачивает около 500 Вт. Более тяжелые нагрузки, например игра в баскетбол, футбол требуют затраты до 700 Вт.

При еще большем возрастании нагрузок ( во время скоростной велосипедной гонки) человек в хорошей физической форме расходует свыше 1000 Вт, однако лишь около 100 Вт из них приходится на внешнюю механическую работу. Подсчитаем, насколько хватит 450 г жира для поддержания умеренных нагрузок (500 Вт). Иными словами, сколько времени должен выполнять физические упражнения человек с избытком веса, чтобы избавиться от 450 г жира?

В одном грамме жира как «топливе» запасено около 40000 Дж энергии. Таким образом, 450 г жира имеют энергию Е = 18 106 Дж. Мощность Р связана с энергией соотношением Р = E/t, отсюда находим: Проделывая в течение 10 ч физические упражнения, можно сбросить 450 г жира, но при этом появляется сильный аппетит.

Другой способ уменьшить избыточный вес состоит в полном отказе от пищи. Тогда для поддержания жизни человеку придется ежедневно расходовать около 300 г своего жирового запаса. Определим, сколько пищевых калорий следует потреблять ежедневно для поддержания жизни. Одна пищевая калория (1 ккал) соответствует 4180 Дж химической энергии. Расходуемая человеком ежедневно минимальная мощность составляет около 80 Вт в состоянии сна и 150 Вт в состоянии бодрствования: будем считать ее равной 110 Вт.

Тогда человеку ежедневно необходима энергия = (110 Вт)(8,6 104 с) = 9,5 106 Дж; она содержится в пище калорийностью 2260 ккал. Такое количество калорий содержится примерно в 400 г жира.

Основные выводы 1. Работа А, совершаемая силой F при перемещении тела из точки А в точку В, дается выражением она измеряется в ньютонах на метр или джоулях;

2. Мощность = (F,v). 3. Кинетическая энергия 4.Теорема о связи работы и энергии:

5.Если F – консервативная сила (или векторная сумма консервативных сил), то приращение потенциальной энергии 6.Для замкнутой системы, содержащей N тел (K + U) = const. 7. Для замкнутой системы, содержащей N тел Р = const.

Лекция окончена Нажмите клавишу для выхода