Презентация на тему: Физика «Гармонические колебания»

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 1. Виды и признаки колебаний 2. Параметры гармонических колебаний 3. Графики смещения скорости и ускорения 4. Основное уравнение динамики гармонических колебаний 5. Энергия гармонических колебаний 6. Гармонический осциллятор 900igr.net

Виды и признаки колебаний В физике особенно выделяют колебания двух видов – механические и электромагнитные и их электромеханические комбинации, поскольку они чрезвычайно актуальны для жизнедеятельности человека. Так, механические колебания плотности воздуха воспринимаются нами как звук, а быстрые электромагнитные колебания – как свет. С помощью звука и света мы получаем основную часть информации об окружающем нас мире. Для колебаний характерно превращение одного вида энергии в другую – кинетической в потенциальную, магнитной в электрическую и т.д. Колебательным движением (или просто колебанием) называются процессы, отличающиеся той или иной степенью повторяемости во времени.

Виды и признаки колебаний Три признака колебательного движения: повторяемость (периодичность) – движение по одной и той же траектории туда и обратно; ограниченность пределами крайних положений; действие силы, описываемой функцией

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Простейшим типом периодических колебаний являются, так называемые, гармонические колебания. Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, ), совершает гармонические колебания.

Саму такую систему часто называют гармоническим осциллятором. Рассмотрение гармонических колебаний важно по двум причинам: колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Периодический процесс можно описать уравнением: . По определению, колебания называются гармоническими, если зависимость некоторой величины имеет вид или Здесь синус или косинус используются в зависимости от условия задачи, А и φ – параметры колебаний, которые мы рассмотрим ниже.

ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Для изучения колебательного движения нам придется ввести несколько терминов – параметров колебательного движения. Расстояние груза от положения равновесия до точки, в которой находится груз, называют смещением x. Максимальное смещение – наибольшее расстояние от положения равновесия – называется амплитудой и обозначается, буквой A.

ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Выражение, являющееся аргументом синуса или косинуса в формуле , определяет смещение x в данный момент времени t и называется фазой колебания. При t=0 φ = φ0 , поэтому называется начальной фазой колебания. Фаза измеряется в радианах и определяет значение колеблющейся величины в данный момент времени. Т.к. синус и косинус изменяются в пределах от +1 до , то -1, то х может принимать значения от +А до –А.

ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Движение от некоторой начальной точки до возвращения в ту же точку называется полным колебанием. Частота колебаний ν определяется, как число полных колебаний в 1 секунду. Частоту, как правило, измеряют в герцах (Гц): 1 Гц равен числу полных колебаний в одну секунду. Очевидно, что

ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Т – период колебаний – минимальный промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание ω – циклическая (круговая) частота – число полных колебаний за 2π секунд. Заметим, что фаза φ не влияет на форму кривой х(t), а влияет лишь на ее положение в некоторый произвольный момент времени t.

ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Колебания характеризуются не только смещением, но и скоростью и ускорением . Если смещение описывается уравнением то, по определению

Графики смещения скорости и ускорения Уравнения колебаний запишем в следующем виде: Из этой системы уравнений можно сделать следующие выводы:

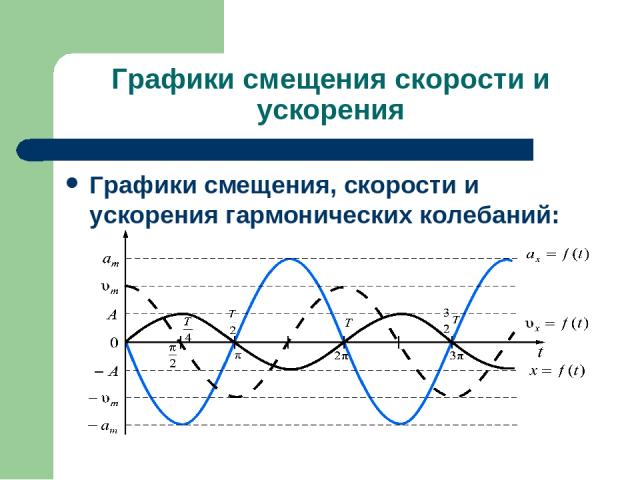
Графики смещения скорости и ускорения Скорость колебаний тела максимальна и, по абсолютной величине, равна амплитуде скорости в момент прохождения через положение равновесия . При максимальном смещении скорость равна нулю; Ускорение равно нулю при прохождении телом положения равновесия и достигает наибольшего значения, равного амплитуде ускорения при наибольших смещениях. Ускорение всегда направленно к положению равновесия, поэтому, удаляясь от положения равновесия, тело двигается замедленно, приближаясь к нему – ускоренно. Ускорение всегда прямо пропорционально смещению, а его направление противоположно направлению смещения. Все эти выводы могут служить определением гармонического колебания.

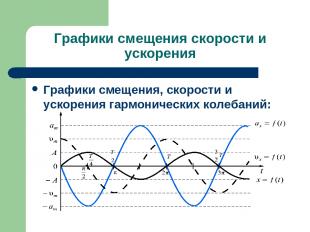
Графики смещения скорости и ускорения Графики смещения, скорости и ускорения гармонических колебаний:

Основное уравнение динамики гармонических колебаний Второй закон Ньютона позволяет, в общем виде, записать связь между силой и ускорением, при прямолинейных гармонических колебаниях материальной точки (или тела) с массой m. Отсюда следует, что сила F пропорциональна х и всегда направлена к положению равновесия (поэтому ее и называют возвращающей силой). Период и фаза силы совпадают с периодом и фазой ускорения.

Основное уравнение динамики гармонических колебаний Примером сил удовлетворяющих этому уравнению являются упругие силы. Силы же имеющие иную природу, но удовлетворяющие этому уравнению называются квазиупругими. Квазиупругая сила Подставляя Fx в основное уравнение получаем:

Основное уравнение динамики гармонических колебаний В случае прямолинейных колебаний вдоль оси х, проекция ускорения на эту ось Подставив выражения для aх и Fх во второй закон Ньютона, получим основное уравнение динамики гармонических колебаний, вызываемых упругими или квазиупругими силами: или

Основное уравнение динамики гармонических колебаний Решение этого уравнения всегда будет выражение вида т.е. смещение груза под действием упругой или квазиупругой силы является гармоническим колебанием, происходящим по синусоидальному закону.

Энергия гармонических колебаний Вычислим энергию тела массой m, совершающего гармонические колебания с амплитудой А и круговой частотой ω. Потенциальная энергия тела U, смещенного на расстояние х от положения равновесия, измеряется той работой, которую произведет возвращающая сила ,перемещая тело в положение равновесия.

Энергия гармонических колебаний Или Кинетическая энергия Тогда

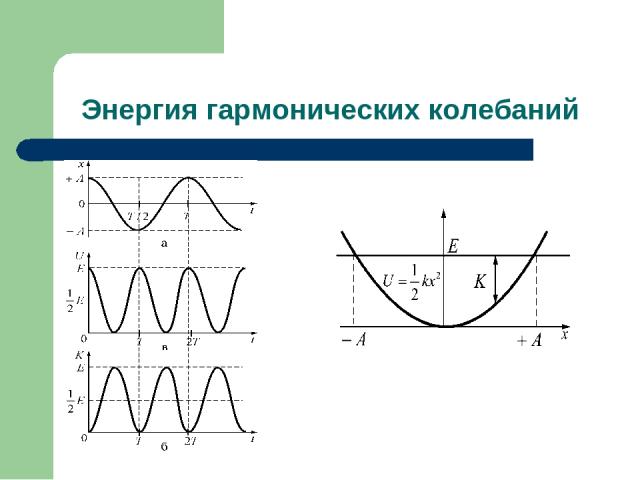
Энергия гармонических колебаний Или Полная механическая энергия гармонически колеблющегося тела пропорциональна квадрату амплитуды колебания. В случае свободных незатухающих колебаний полная энергия не зависит от времени, поэтому и амплитуда А – не зависит от времени.

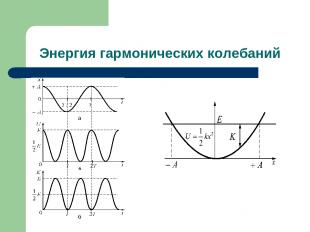
Энергия гармонических колебаний

Гармонические осцилляторы Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классической и квантовой физики. Примерами гармонического осциллятора являются пружинный, математический и физический маятники, а также колебательный контур (для малых токов и напряжений).

Гармонические осцилляторы Пружинный маятник или Математический маятник ( только для малых колебаний )

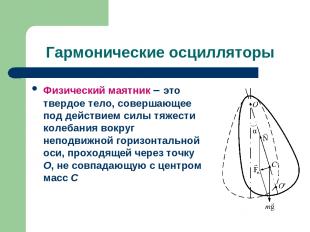
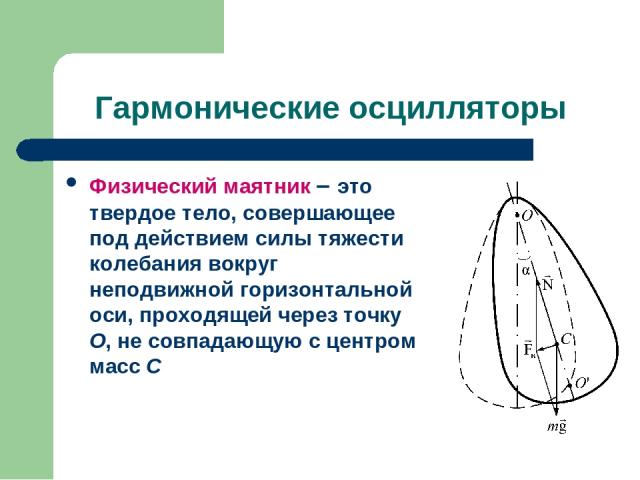
Гармонические осцилляторы Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С

Гармонические осцилляторы При отклонении этого тела от положения равновесия на угол α, также возникает вращающий момент, стремящийся вернуть маятник в положение равновесия: где l – расстояние между точкой подвеса и центром масс маятника С. Обозначим через J – момент инерции маятника относительно точки подвеса O.

Гармонические осцилляторы Тогда В случае малых колебаний Величину момента инерции J иногда бывает трудно вычислить.

Гармонические осцилляторы Сопоставляя формулы для периода колебаний физического и математического маятников, можно обозначить: где – приведенная длина физического маятника – это длина такого математического маятника, период колебания которого совпадает с периодом колебаний данного физического маятника.

ВЛИЯНИЕ ВНЕШНИХ СИЛ НА КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ 1. Свободные затухающие механические колебания 2. Коэффициент затухания и логарифмический декремент затухания 3. Вынужденные механические колебания 4. Автоколебания

Затухающие колебания Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается. Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например, маятник).

Затухающие колебания Тогда сила трения (или сопротивления) Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x Или Введем обозначения

Затухающие колебания Тогда однородное дифференциальное уравнение второго порядка запишется так: Решение этого уравнения имеет вид при А0 и φ0 – определяются из краевых условий (начальных и граничных) задачи. β и ω – из самого уравнения.

Затухающие колебания Найдем ω. Здесь оно уже не равно . Подставим решение дифференциального уравнения в само дифференциальное уравнение продифференцировав решение один и два раза по времени. Тогда имеем: или где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний.

Затухающие колебания Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω – циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и называется условным периодом затухающих колебаний.

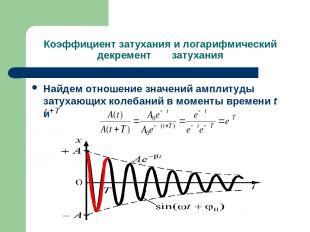
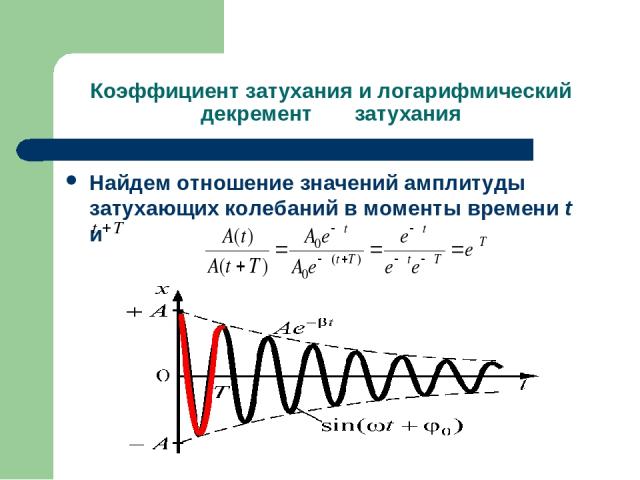
Коэффициент затухания и логарифмический декремент затухания Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и

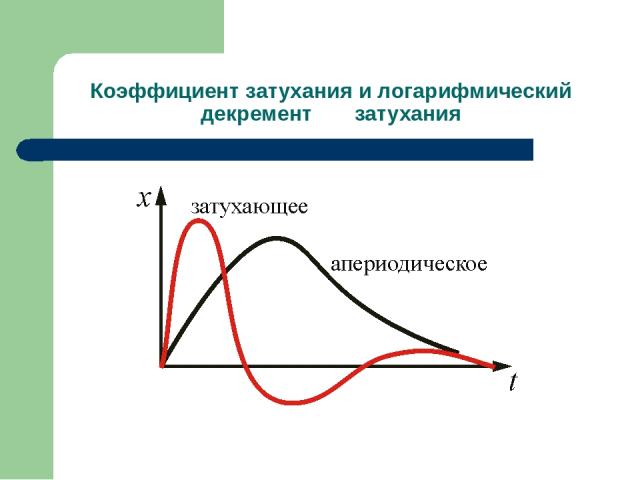
Коэффициент затухания и логарифмический декремент затухания Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания. Выясним физический смысл χ и β. Обозначим через τ – время, в течение которого амплитуда А уменьшается в e раз. откуда

Коэффициент затухания и логарифмический декремент затухания Следовательно, коэффициент затухания β – есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз, τ – время релаксации. Пусть N число колебаний, после которых амплитуда уменьшается в e – раз. Тогда

Коэффициент затухания и логарифмический декремент затухания Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечению которых амплитуда А уменьшается в e раз. Если χ = 0,01 то N = 100. При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому , то процесс будет апериодическим .

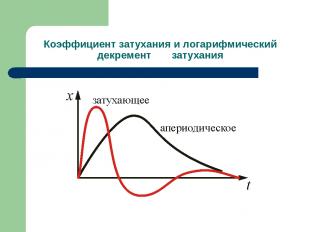
Коэффициент затухания и логарифмический декремент затухания

Вынужденные механические колебания Рассмотрим систему, на которую кроме упругой силы (– kx) и сил сопротивления (– rυ) действует добавочная периодическая сила F – вынуждающая сила. Для колебаний вдоль оси x запишем основное уравнение колебательного процесса, или где fх = Fх/m – вынуждающая сила, изменяющаяся по гармоническому закону:

Вынужденные механические колебания Через некоторое время после начала действия вынуждающей силы колебания системы будут совершаться с частотой вынуждающей силы, ω. Уравнение установившихся вынужденных колебаний Наша задача найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждающей силой.

Вынужденные механические колебания Обратим внимание на то, что скорость на π/2 опережает смещение, а ускорение на π/2 опережает скорость. Преобразуем и через косинус:

Вынужденные механические колебания Обозначим – угол между смещением и вынуждающей силой. Подставим все эти выражения в дифференциальное уравнение для вынужденных колебаний и получаем в итоге: или

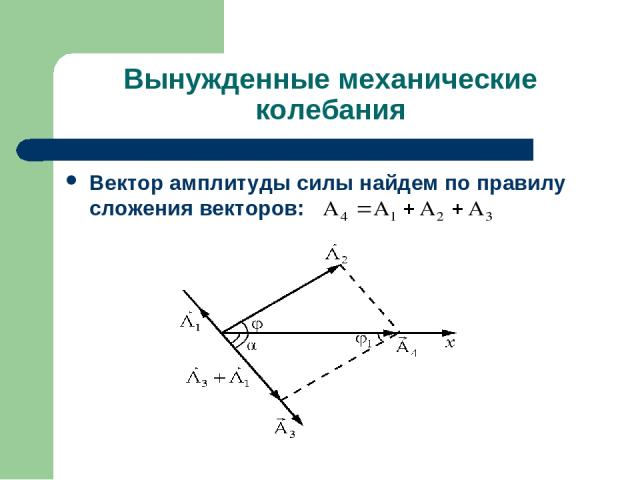
Вынужденные механические колебания Каждое слагаемое последнего уравнения можно представить в виде соответствующего вращающегося вектора амплитуды: амплитуда ускорения, амплитуда скорости, амплитуда смещения, амплитуда вынуждающей силы, причем

Вынужденные механические колебания Вектор амплитуды силы найдем по правилу сложения векторов:

Вынужденные механические колебания Из рисунка видно, что Найдем амплитуду А: Таким образом, и .

Вынужденные механические колебания При постоянных F0, m и β – амплитуда зависит только от соотношения круговых частот вынуждающей силы ω и свободных незатухающих колебаний системы ω0. Начальную фазу вынужденных колебаний можно найти из выражения:

Вынужденные механические колебания Из рисунка видно, что сила опережает смещение на угол, который определяется из выражения: Проанализируем выражение для амплитуды. (частота вынуждающей силы равна нулю), тогда Статическая амплитуда, колебания не совершаются.

Вынужденные механические колебания 2. Затухания нет С увеличением ω (но при ), амплитуда растет и при , амплитуда резко возрастает ( ). Это явление называется – резонанс. При дальнейшем увеличении ( ) амплитуда опять уменьшается.

Вынужденные механические колебания Если амплитуда будет максимальна при минимальном значении знаменателя. Для нахождения точки перегиба возьмем первую производную по ω от подкоренного выражения и приравняем ее к нулю. Тогда резонансная частота будет определяться выражением:

ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ 1. Квазистационарные токи 2. Свободные колебания в электрическом контуре без активного сопротивления 3. Свободные затухающие электрические колебания 4. Вынужденные электрические колебания 5. Мощность, выделяемая в цепи переменного тока

Квазистационарные токи При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися во времени. Закон Ома и вытекающие из него правила Кирхгофа, были установлены для постоянного тока. Однако, они остаются справедливыми и для мгновенных значений изменяющихся тока и напряжения, если их изменения происходят не слишком быстро. Электромагнитные сигналы распространяются по цепи со скоростью света с.

Квазистационарные токи Пусть l – длина электрической цепи. Тогда время распространения сигнала в данной цепи Если (T – период колебаний электрического тока), то такие токи называются квазистационарными. При этом условии мгновенное значение силы тока во всех участках цепи будет постоянным. Для частоты условие квазистационарности выполняется при длине цепи ~ 100 км.

Свободные колебания в электрическом контуре без активного сопротивления В цепи, содержащей индуктивность L и ёмкость С могут возникать электрические колебания. Такая цепь называется колебательным контуром

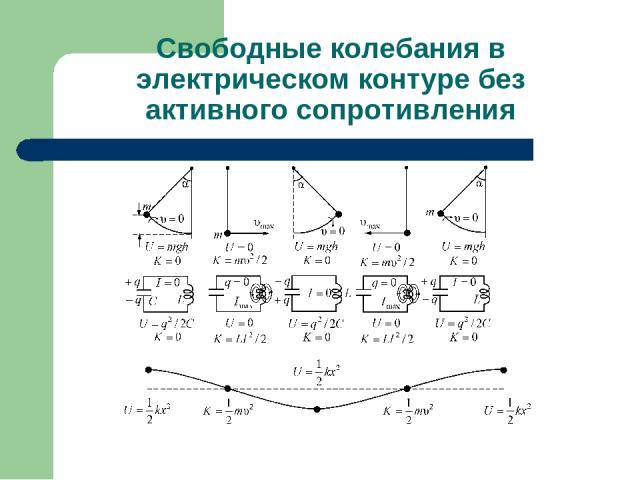
Свободные колебания в электрическом контуре без активного сопротивления Поскольку активное сопротивление контура , полная энергия остаётся постоянной. Если энергия конденсатора равна нулю, то энергия магнитного поля максимальна и наоборот. Рассмотрим процессы, происходящие в колебательном контуре в сравнении с колебаниями маятника .

Свободные колебания в электрическом контуре без активного сопротивления

Свободные колебания в электрическом контуре без активного сопротивления Из сопоставления электрических и механических колебаний следует, что, энергия электрического поля аналогична потенциальной энергии, а энергия магнитного поля аналогична кинетической энергии; L играет роль массы т, а 1/С – роль коэффициента жесткости k. Наконец заряду q соответствует смещение маятника из положения равновесия х, силе тока I – скорость υ, а напряжению U – ускорение а.

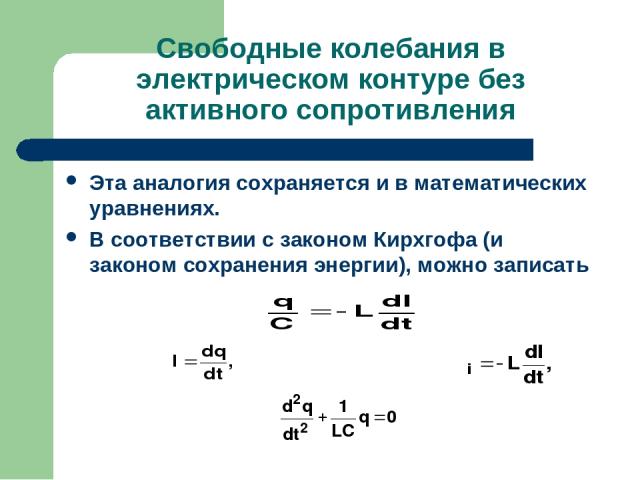
Свободные колебания в электрическом контуре без активного сопротивления Эта аналогия сохраняется и в математических уравнениях. В соответствии с законом Кирхгофа (и законом сохранения энергии), можно записать

Свободные колебания в электрическом контуре без активного сопротивления Введем обозначение: – собственная частота контура, отсюда получим основное уравнение колебаний в контуре: Решением этого уравнения является выражение вида:

Свободные колебания в электрическом контуре без активного сопротивления Таким образом, заряд на обкладке конденсатора изменяется по гармоническому закону с собственной частотой контура – ω0. Для периода колебаний справедлива, так называемая формула Томсона:

Свободные колебания в электрическом контуре без активного сопротивления Продифференцируем по времени выражение для заряда и получим выражение для тока: Напряжение на конденсаторе отличается от заряда множителем 1/С:

Свободные колебания в электрическом контуре без активного сопротивления Максимальные значения

Свободные затухающие электрические колебания Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего колебания затухают.

Свободные затухающие электрические колебания По второму закону Кирхгофа Обозначив – коэффициент затухания; получим уравнение затухающих колебаний в контуре с R, L и С:

Свободные затухающие электрические колебания При т.е. , решение этого уравнения имеет вид: Затухание принято характеризовать логарифмическим декрементом затухания

Свободные затухающие электрические колебания Колебательный контур часто характеризуют добротностью Q, которая определяется как величина, обратно пропорциональная χ: Добротность определяется и по другому: где W – энергия контура в данный момент, ΔW – убыль энергии за один период, следующий за этим моментом. , ,

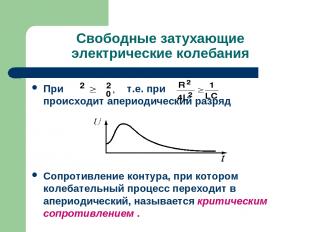
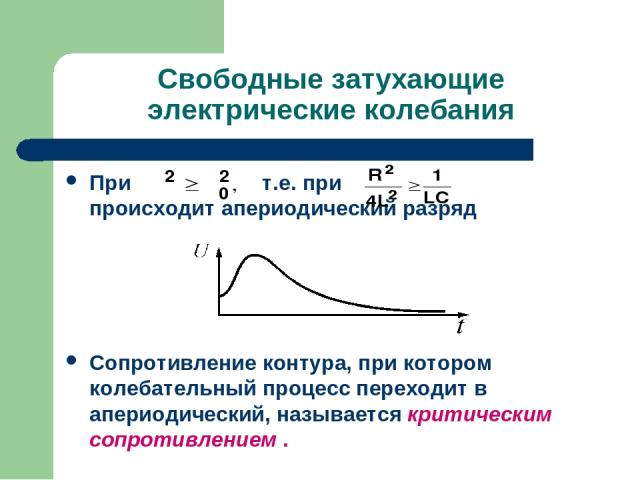
Свободные затухающие электрические колебания При т.е. при происходит апериодический разряд Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим сопротивлением .

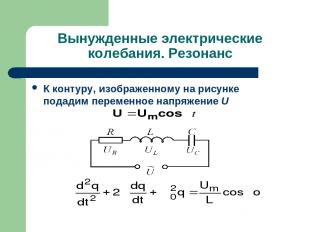
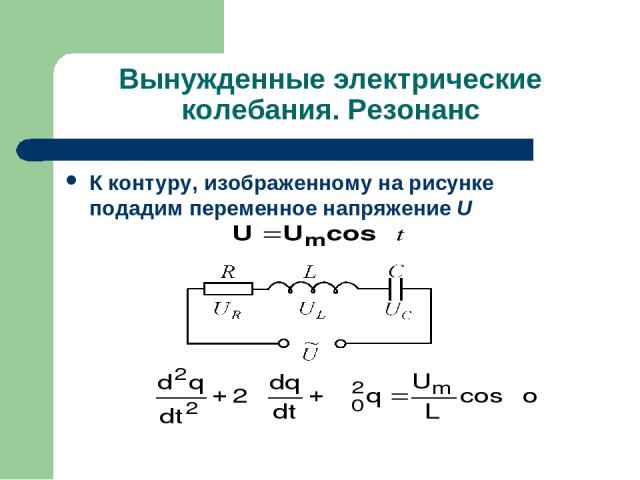
Вынужденные электрические колебания. Резонанс К контуру, изображенному на рисунке подадим переменное напряжение U

Вынужденные электрические колебания. Резонанс Это уравнение вынужденных электрических колебаний, которое совпадает с аналогичным уравнением механических колебаний. Его решение имеет вид: Величина называется полным сопротивлением контура

Вынужденные электрические колебания. Резонанс При последовательном соединении R, L, С, в контуре когда – наблюдается резонанс. При этом угол сдвига фаз между током и напряжением обращается в нуль (φ = 0). Резонансная частота при напряжении на конденсаторе Uс равна

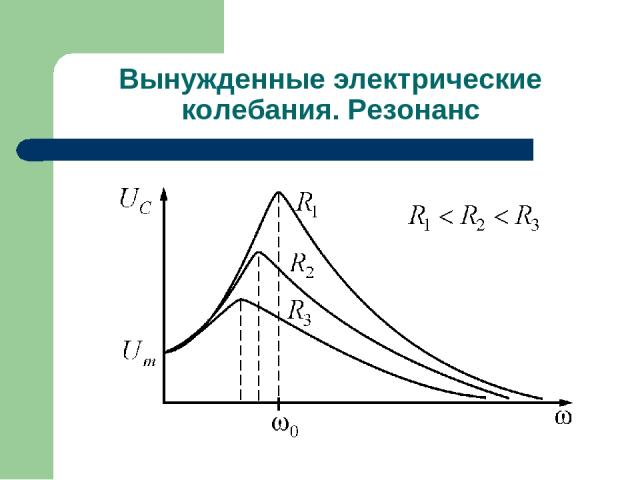
Вынужденные электрические колебания. Резонанс Тогда , а Uс и UL одинаковы по амплитуде и противоположны по фазе. Такой вид резонанса называется резонансом напряжения или последовательным резонансом. Резонансные кривые для напряжения U изображены на рисунке. Они сходны с резонансными кривыми для ускорения a при механических колебаниях.

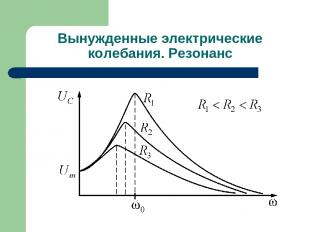
Вынужденные электрические колебания. Резонанс

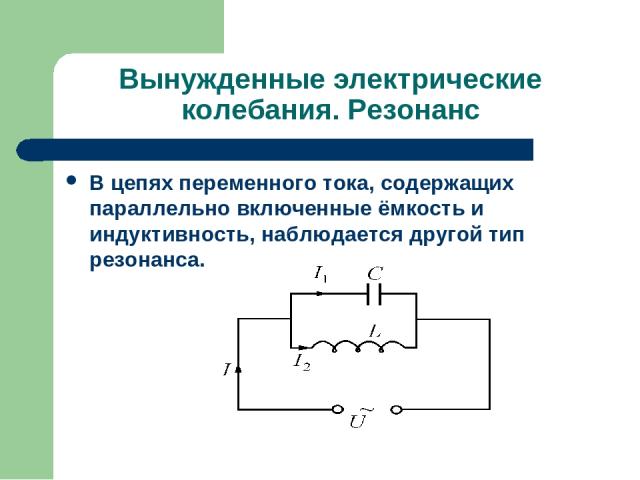
Вынужденные электрические колебания. Резонанс В цепях переменного тока, содержащих параллельно включенные ёмкость и индуктивность, наблюдается другой тип резонанса.

Вынужденные электрические колебания. Резонанс

Вынужденные электрические колебания. Резонанс