Презентация на тему: Электротехника и электроника

Дисциплина: Электротехника и электроника Лектор: Валерий Петрович Довгун доктор технических наук, профессор 900igr.net

САМОСТОЯТЕЛЬНАЯ РАБОТА: 1. Расчетно-графическое задание. 2. Подготовка к выполнению и защите лабораторных работ. 3. Самостоятельное изучение отдельных разделов курса. Электротехника и электроника * АУДИТОРНЫЕ ЗАНЯТИЯ: Лекции, практические задания, лабораторные работы

Электротехника и электроника ИТОГОВАЯ АТТЕСТАЦИЯ Третий семестр: зачет. Четвертый семестр: экзамен. *

Электротехника и электроника Рекомендуемая литература Новожилов, О. П. Электротехника и электроника: учебник / О. П. Новожилов. – М.: Гардарики, 2008. – 653 с. Довгун, В. П. Электротехника и электроника: учеб. пособие: в 2-х ч. Ч. 1 / В. П. Довгун. – Красноярск: ИПЦ КГТУ, 2006. – 270 с. Довгун, В. П. Электротехника и электроника: учеб. пособие: в 2-х ч. Ч. 2 / В. П. Довгун. – Красноярск: ИПЦ КГТУ, 2006. – 252 с. *

Электротехника и электроника Электрические величины и единицы их измерения Единица измерения тока в системе СИ – ампер (А). Ток в проводящей среде – явление упорядоченного движения электрических зарядов под действием электрического поля. Мгновенное значение тока равно скорости изменения заряда во времени: *

Единица измерения напряжения в системе СИ – вольт (В). Напряжение (разность потенциалов) между двумя точками цепи определяется количеством энергии, затрачиваемой на перемещение заряда из одной точки в другую: Электрические величины и единицы их измерения *

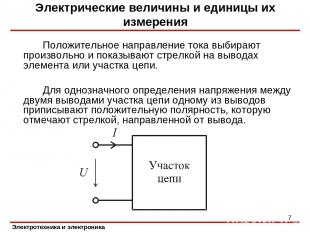
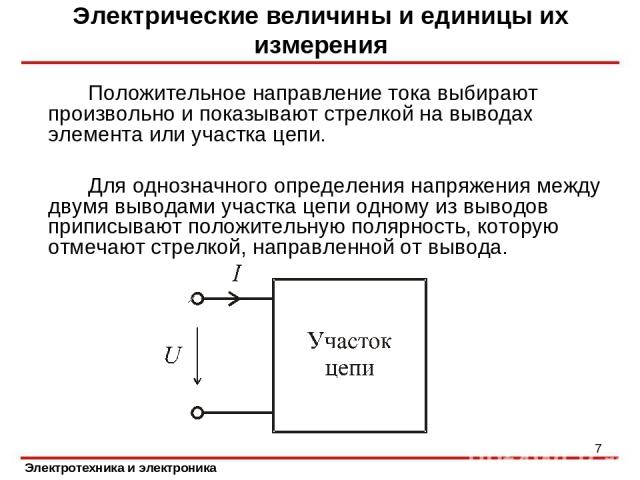
Электрические величины и единицы их измерения Положительное направление тока выбирают произвольно и показывают стрелкой на выводах элемента или участка цепи. Для однозначного определения напряжения между двумя выводами участка цепи одному из выводов приписывают положительную полярность, которую отмечают стрелкой, направленной от вывода. Электротехника и электроника *

Энергия, затрачиваемая на перемещение заряда Мгновенная мощность участка цепи: Электрические величины и единицы их измерения * Мощность измеряется в ваттах (Вт).

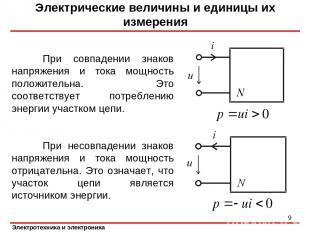
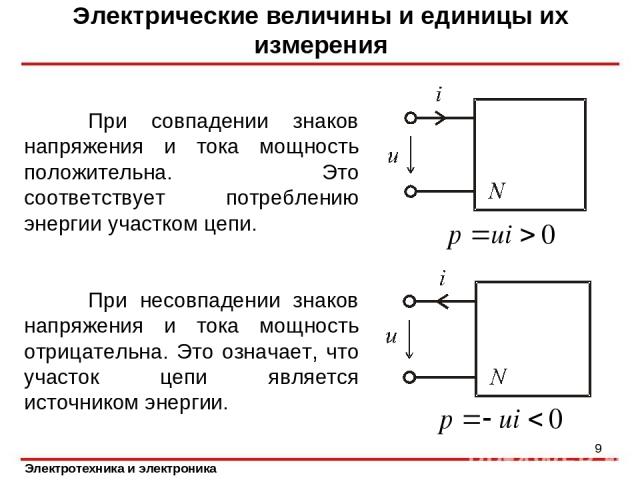
При совпадении знаков напряжения и тока мощность положительна. Это соответствует потреблению энергии участком цепи. При несовпадении знаков напряжения и тока мощность отрицательна. Это означает, что участок цепи является источником энергии. Электрические величины и единицы их измерения *

Элементы электрических цепей Под элементами в теории цепей понимают не реальные устройства, а их идеализированные модели, обладающие определенными свойствами реальных прототипов. Такими идеализированными элементами являются резистивный, индуктивный и емкостный элементы, а также независимые источники напряжения и тока. Соединяя между собой идеализированные элементы, мы получим модель, или схему замещения, приближенно отображающую процессы в реальном электронном устройстве.

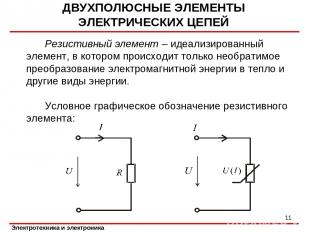
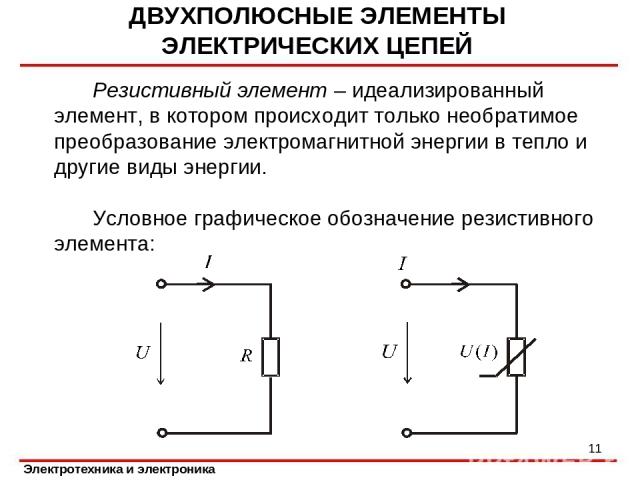
ДВУХПОЛЮСНЫЕ ЭЛЕМЕНТЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ Резистивный элемент – идеализированный элемент, в котором происходит только необратимое преобразование электромагнитной энергии в тепло и другие виды энергии. Условное графическое обозначение резистивного элемента: *

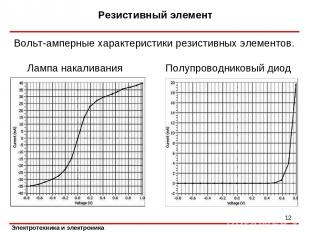
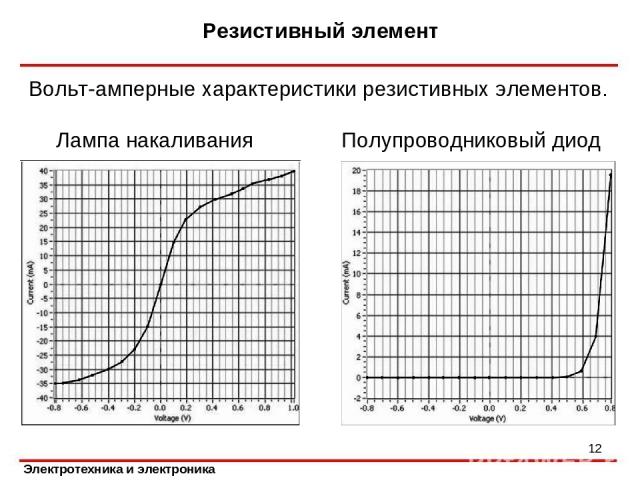
Вольт-амперные характеристики резистивных элементов. Резистивный элемент * Полупроводниковый диод Лампа накаливания

Если ВАХ – прямая, проходящая через начало координат, резистор называют линейным. Закон Ома: R – сопротивление. Единица измерения – Ом. Резистивный элемент *

Закон Ома: - проводимость. Единица измерения – Сименс. Мощность, поглощаемая резистором Резистивный элемент *

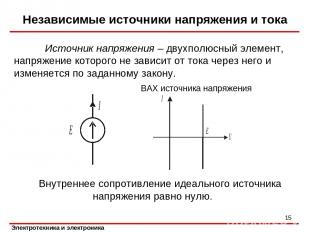
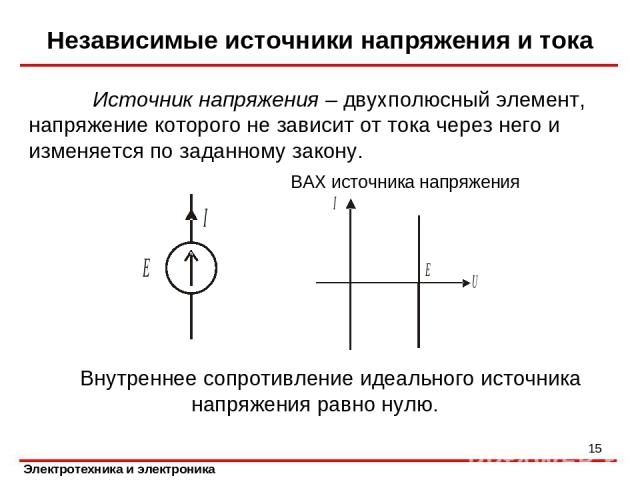
Независимые источники напряжения и тока Внутреннее сопротивление идеального источника напряжения равно нулю. Источник напряжения – двухполюсный элемент, напряжение которого не зависит от тока через него и изменяется по заданному закону. ВАХ источника напряжения *

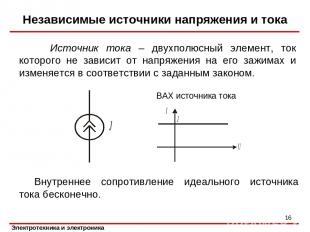
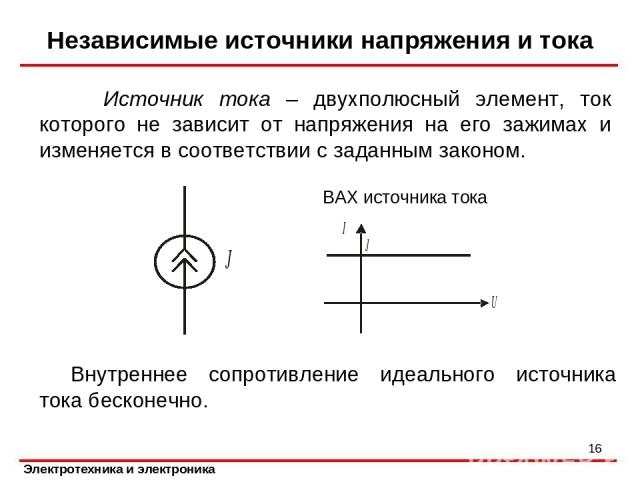
Источник тока – двухполюсный элемент, ток которого не зависит от напряжения на его зажимах и изменяется в соответствии с заданным законом. Внутреннее сопротивление идеального источника тока бесконечно. Независимые источники напряжения и тока * ВАХ источника тока

Управляемые источники Управляемый источник – четырехполюсный резистивный элемент, состоящий из двух ветвей и двух пар выводов: входной и выходной. Управляемые источники обладают следующими свойствами: 1) выходная величина пропорциональна входной. 2) выходная величина не влияет на входную. *

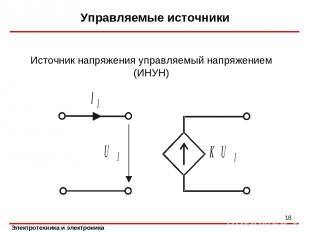
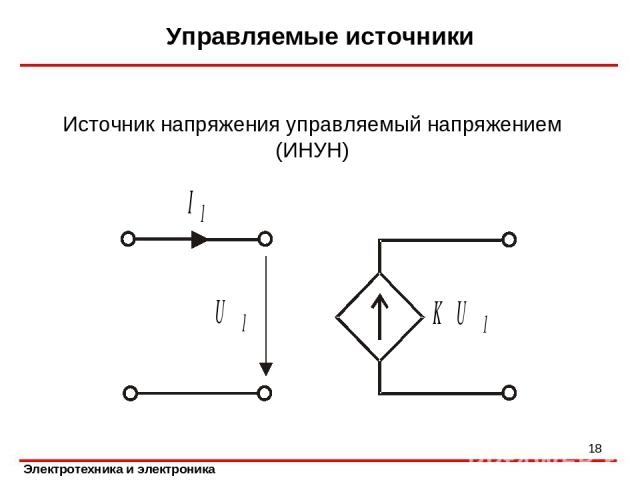
Управляемые источники * Источник напряжения управляемый напряжением (ИНУН)

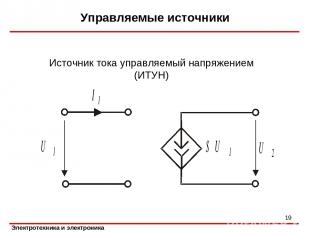
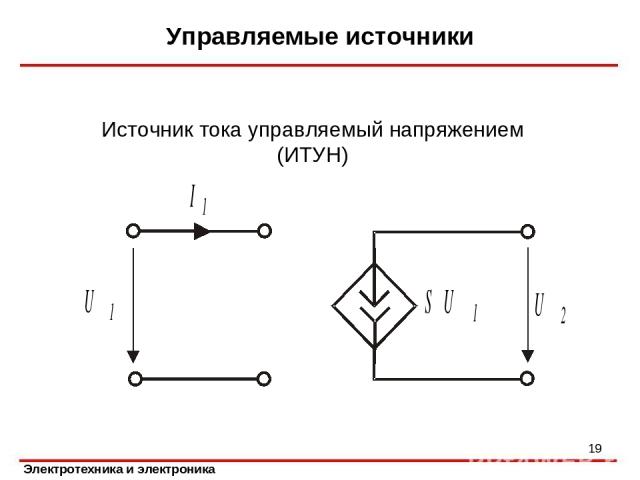
Управляемые источники * Источник тока управляемый напряжением (ИТУН)

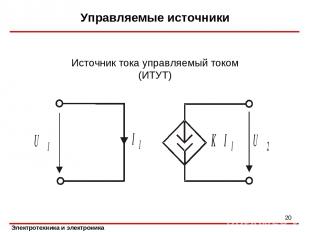
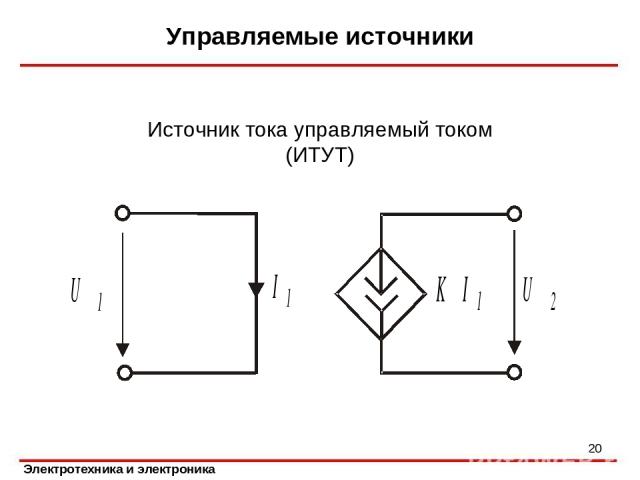
Управляемые источники * Источник тока управляемый током (ИТУТ)

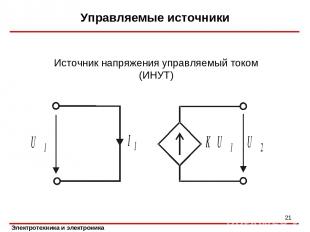
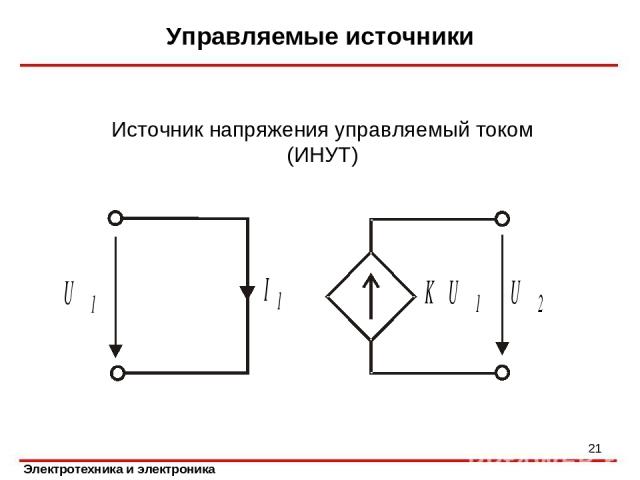
Управляемые источники * Источник напряжения управляемый током (ИНУТ)

Выводы * Ток в проводящей среде есть явление упорядоченного движения электрических зарядов под действием электрического поля. Мгновенное значение тока равно скорости изменения заряда во времени. Положительное направление тока выбирают произвольно и показывают стрелкой на выводах элемента или участка цепи. 2. Напряжение (разность потенциалов) между двумя точками цепи определяется количеством энергии, затрачиваемой на перемещение заряда из одной точки в другую. Положительное направление напряжения показывают стрелкой, направленной от одного зажима элемента к другому, либо знаками «+», «-»

Выводы * 3. Для обозначения электрических величин используют прописные и строчные буквы. Прописными буквами обозначают постоянные напряжения, токи и мощности: U, I, P. Мгновенные значения переменных величин обозначают малыми (строчными) буквами: u, i, p. Резистивным называют идеализированный двухполюсный элемент, для которого связь между напряжением и током можно представить в виде графика, называемого вольт-амперной характеристикой (ВАХ). Резистивный элемент моделирует процесс необратимого преобразования электромагнитной энергии в тепло и другие виды энергии, при этом запасание энергии в электромагнитном поле отсутствует.

Выводы * 5. Источник напряжения – двухполюсный элемент, напряжение которого не зависит от тока через него и изменяется по заданному закону. Внутренне сопротивление идеального источника напряжения равна нулю. 6. Источник тока - двухполюсный элемент, ток которого не зависит от напряжения на его зажимах и изменяется в соответствии с заданным законом. Внутренне сопротивление идеального источника тока бесконечно.

Задача анализа электрических цепей. Законы Кирхгофа Основные топологические понятия Ветвь – участок цепи с двумя выводами. Узел – точка соединения двух или более ветвей. Контур – замкнутый путь, проходящий через ряд ветвей и узлов. *

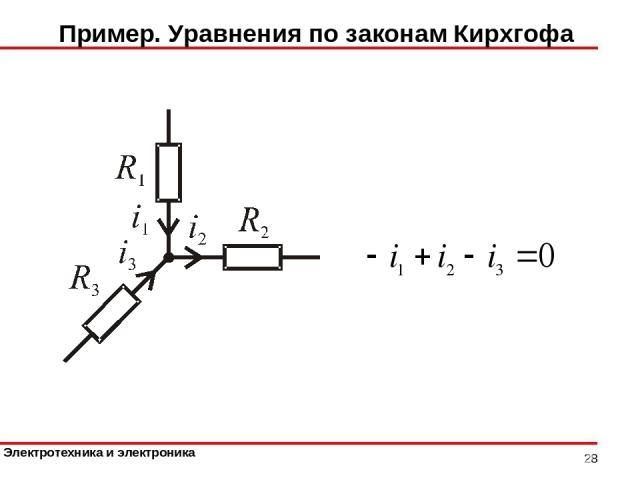
Законы Кирхгофа Первый закон Кирхгофа: Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю: Токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус. Число независимых уравнений по первому закону Кирхгофа *

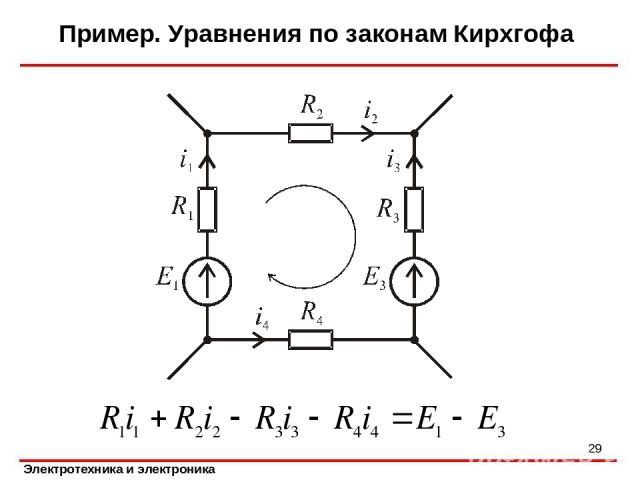
Законы Кирхгофа Второй закон Кирхгофа: В контуре электрической цепи алгебраическая сумма напряжений ветвей равна алгебраической сумме ЭДС источников. Число независимых уравнений по второму закону Кирхгофа, равно числу независимых контуров: *

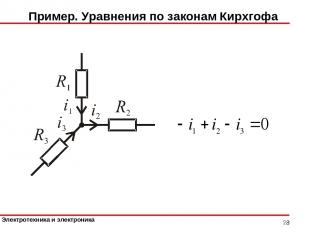
Пример. Уравнения по законам Кирхгофа *

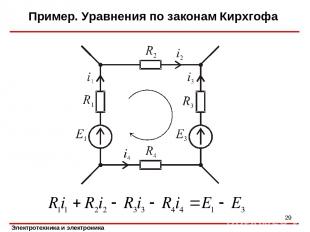
Пример. Уравнения по законам Кирхгофа *

Принцип наложения (суперпозиции). Метод наложения Принцип наложения является фундаментальным свойством линейных цепей. Реакция линейной цепи при одновременном действии нескольких независимых источников равна сумме реакций, получающихся при действии каждого источника в отдельности. Принцип наложения является следствием линейности уравнений, описывающих цепь. Принцип наложения справедлив только для линейных цепей. *

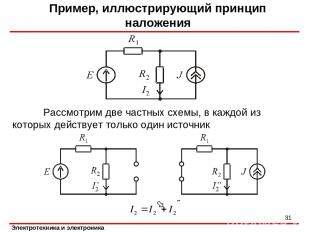
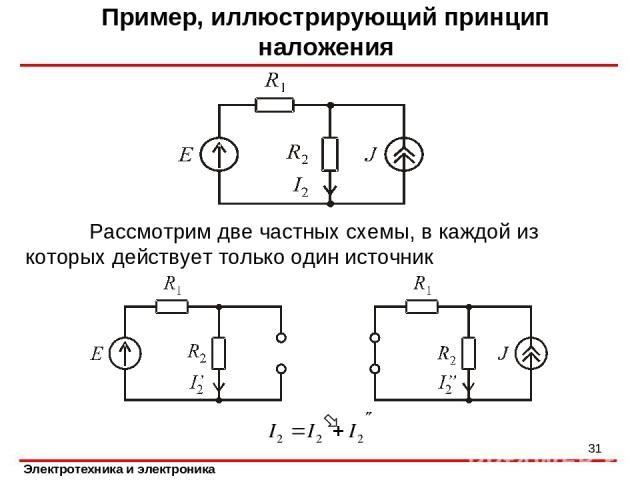
Пример, иллюстрирующий принцип наложения Рассмотрим две частных схемы, в каждой из которых действует только один источник *

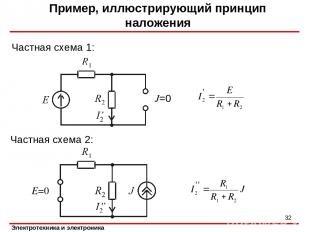
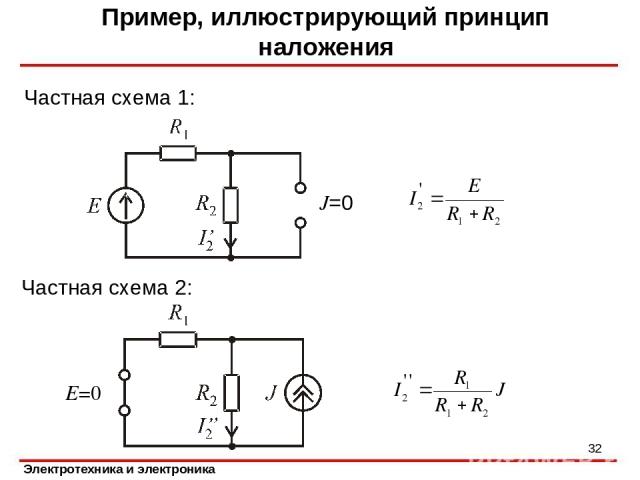
Пример, иллюстрирующий принцип наложения Частная схема 1: * J=0 E=0 Частная схема 2:

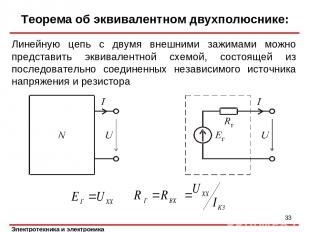
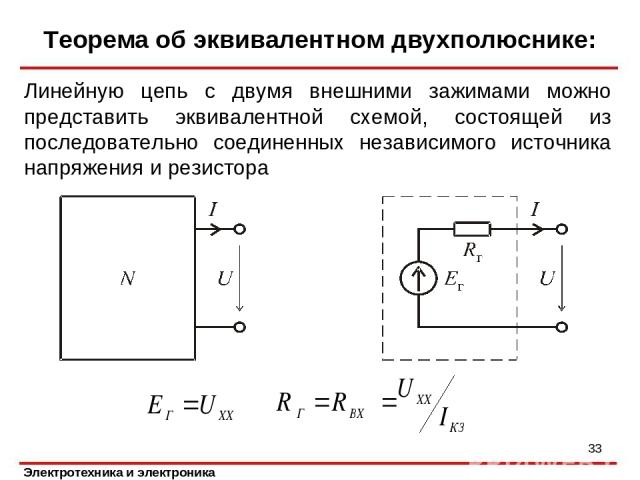
Теорема об эквивалентном двухполюснике: Линейную цепь с двумя внешними зажимами можно представить эквивалентной схемой, состоящей из последовательно соединенных независимого источника напряжения и резистора *

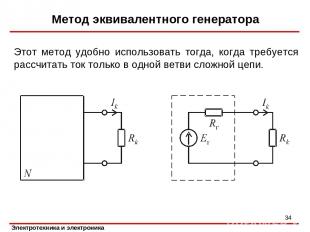
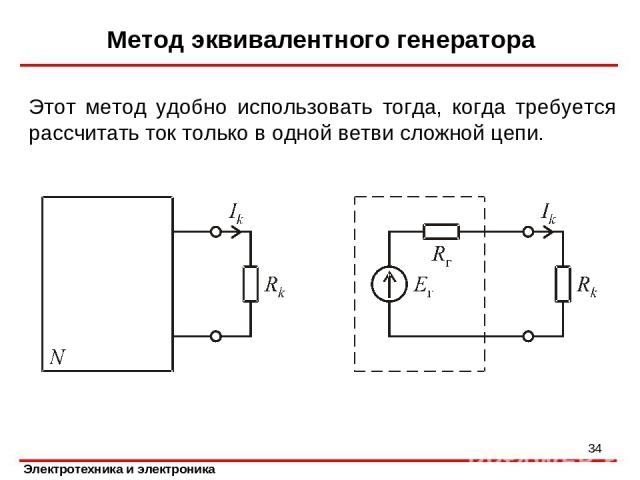
Метод эквивалентного генератора Этот метод удобно использовать тогда, когда требуется рассчитать ток только в одной ветви сложной цепи. *

Последовательность расчета методом эквивалентного генератора Выделяем ветвь, в которой необходимо рассчитать ток, а остальную часть цепи заменяем эквивалентным двухполюсником. Определяем параметры эквивалентного двухполюсника Искомый ток рассчитываем по формуле *

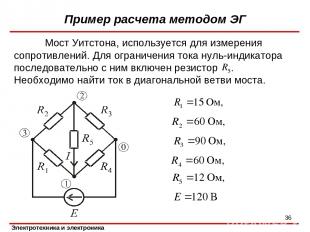
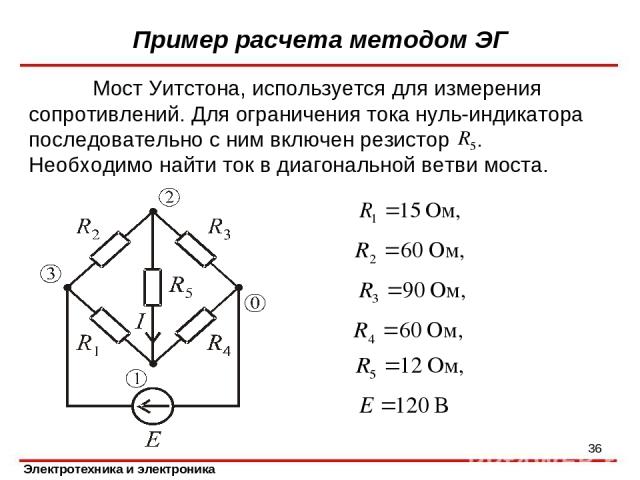
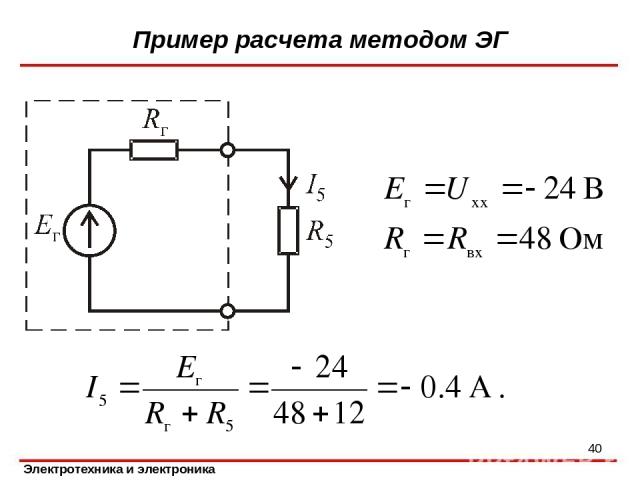
Пример расчета методом ЭГ Мост Уитстона, используется для измерения сопротивлений. Для ограничения тока нуль-индикатора последовательно с ним включен резистор . Необходимо найти ток в диагональной ветви моста. *

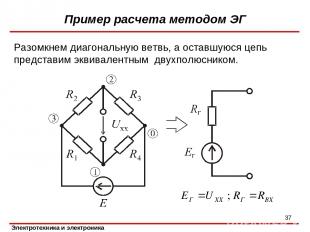
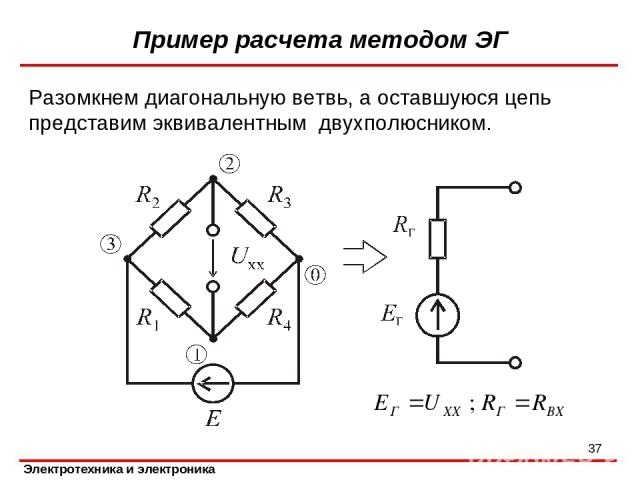
Разомкнем диагональную ветвь, а оставшуюся цепь представим эквивалентным двухполюсником. Пример расчета методом ЭГ *

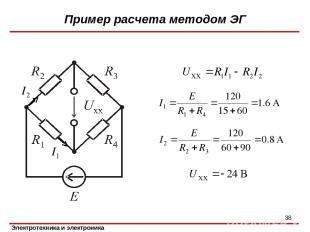
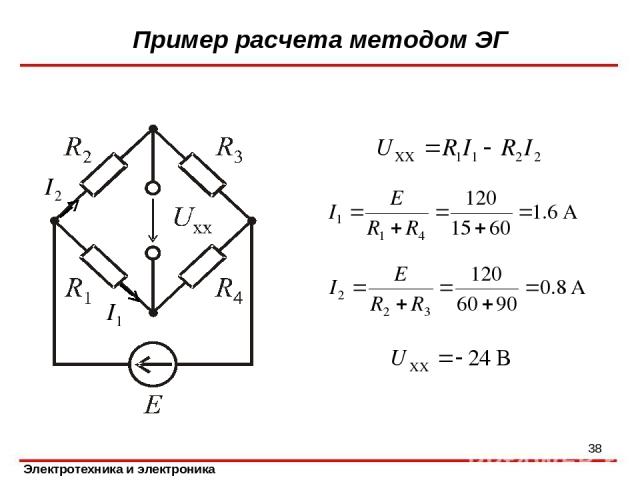
Пример расчета методом ЭГ *

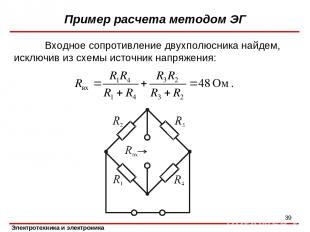
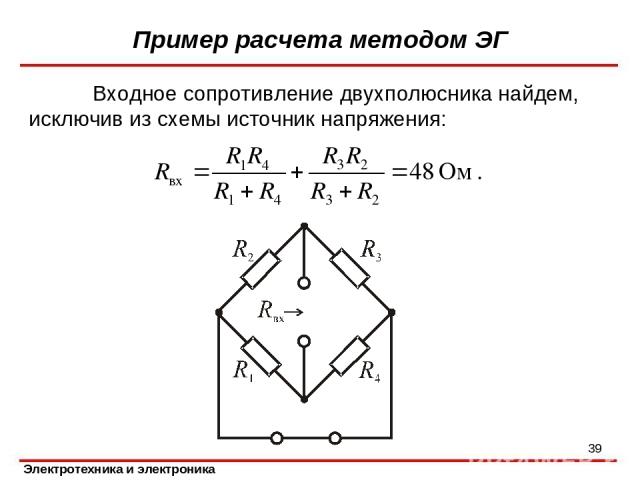
Входное сопротивление двухполюсника найдем, исключив из схемы источник напряжения: Пример расчета методом ЭГ *

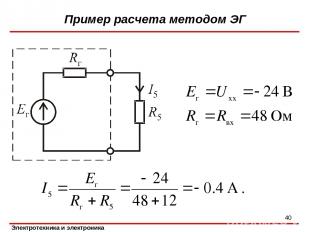
Пример расчета методом ЭГ *

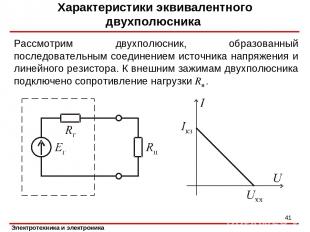
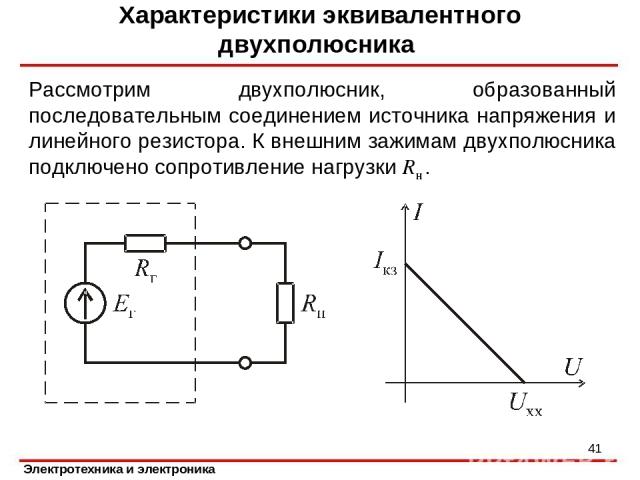
Характеристики эквивалентного двухполюсника Рассмотрим двухполюсник, образованный последовательным соединением источника напряжения и линейного резистора. К внешним зажимам двухполюсника подключено сопротивление нагрузки Rн . *

Характеристики эквивалентного двухполюсника Ток в цепи Напряжение на зажимах двухполюсника * Мощность, отдаваемая двухполюсником в сопротивление нагрузки

Режим короткого замыкания В режиме к. з. Pн=0 . Режим холостого хода: напряжение на внешних зажимах двухполюсника равно напряжению источника: а ток I = 0 Характеристики эквивалентного двухполюсника * В режиме хх Pн=0 .

Двухполюсник отдает в нагрузку максимальную мощность при : Этот режим называют режимом согласованной нагрузки. Характеристики эквивалентного двухполюсника *

Операционные усилители Операционный усилитель (ОУ) – усилитель, имеющий большой коэффициент усиления, высокое входное и малое выходное сопротивления. В настоящее время операционные усилители выпускают в виде интегральных микросхем. * Типичные параметры интегрального ОУ: , В линейном режиме коэффициент усиления напряжения ОУ KU = 104–106.

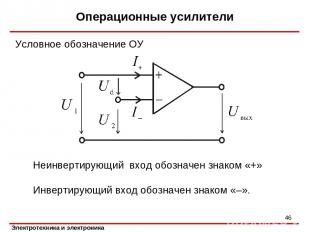
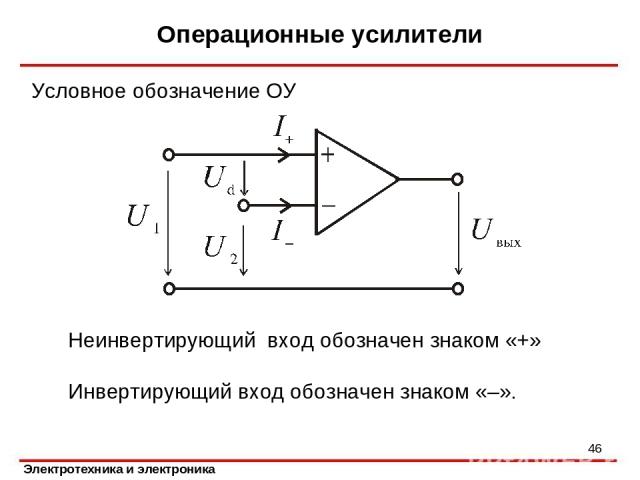
Операционные усилители Условное обозначение ОУ * Неинвертирующий вход обозначен знаком «+» Инвертирующий вход обозначен знаком «–».

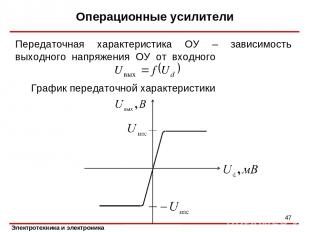
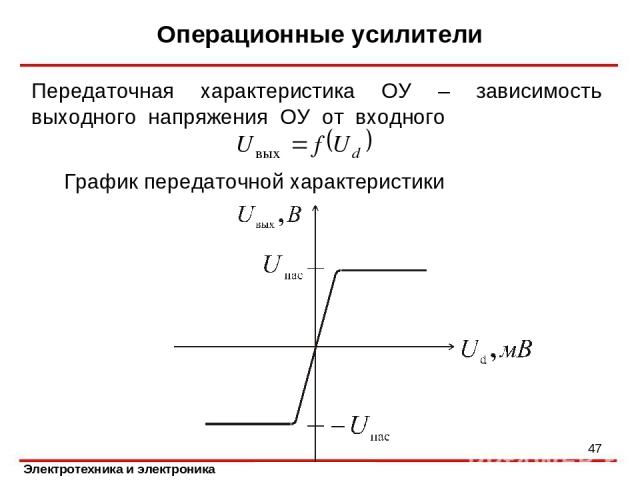
Операционные усилители Передаточная характеристика ОУ – зависимость выходного напряжения ОУ от входного * График передаточной характеристики

Анализ цепей с ОУ Правила анализа электронных цепей с ОУ, работающими в линейном режиме. * 1. Входные токи ОУ равны нулю: 2. Напряжение на входе ОУ равно нулю: (правило виртуального короткого замыкания). Правило виртуального короткого замыкания справедливо только в том случае, если ОУ охвачен отрицательной обратной связью и его выходное напряжение меньше напряжения насыщения.

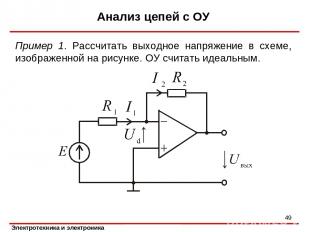
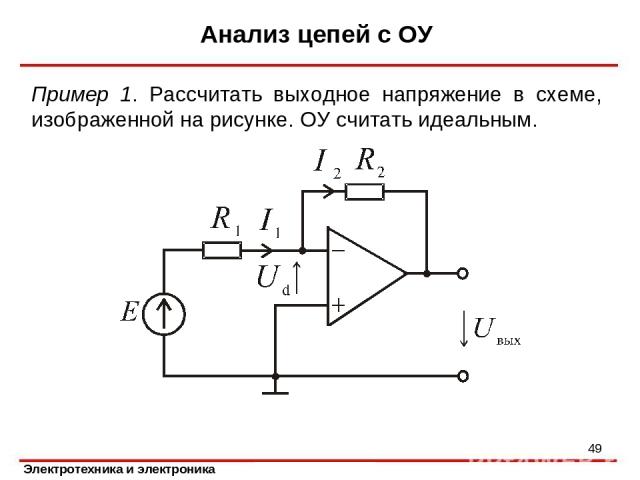
Анализ цепей с ОУ Пример 1. Рассчитать выходное напряжение в схеме, изображенной на рисунке. ОУ считать идеальным. *

Анализ цепей с ОУ Запишем уравнение по первому закону Кирхгофа для узла 1: * Уравнение по второму закону Кирхгофа для контура, включающего источник E, резистор R1 и вход ОУ: Для контура, включающего вход ОУ, резистор R2 и выход схемы, имеем

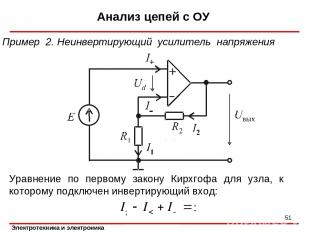
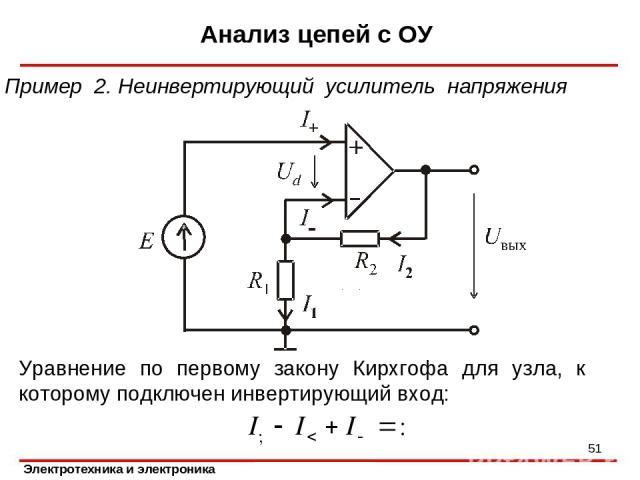
Анализ цепей с ОУ * Пример 2. Неинвертирующий усилитель напряжения Уравнение по первому закону Кирхгофа для узла, к которому подключен инвертирующий вход:

Анализ цепей с ОУ * Уравнение по второму закону Кирхгофа для контура, включающего источник E, резистор R1 и вход ОУ: Для контура, включающего резисторы R1, R2 и выход схемы, имеем Решая эту систему уравнений и учитывая, что получаем

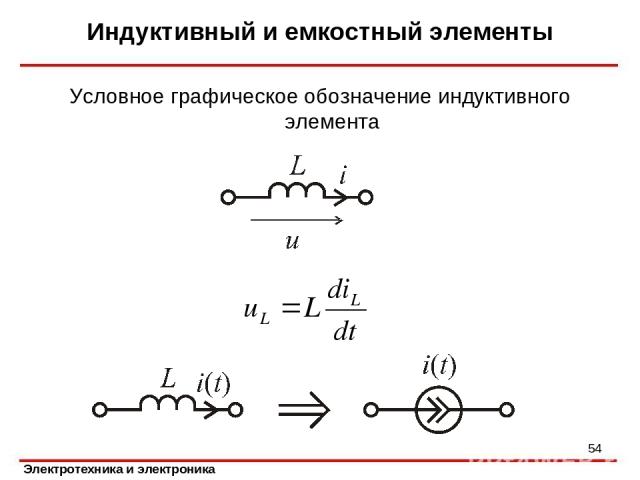
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Индуктивный и емкостный элементы В индуктивном элементе происходит запасание энергии, связанное с прохождением тока, потери и запасание электрической энергии отсутствуют. Условное графическое обозначение индуктивного элемента *

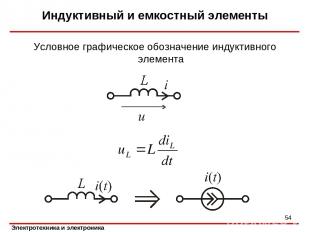
Индуктивный и емкостный элементы Условное графическое обозначение индуктивного элемента *

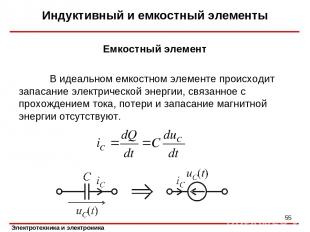
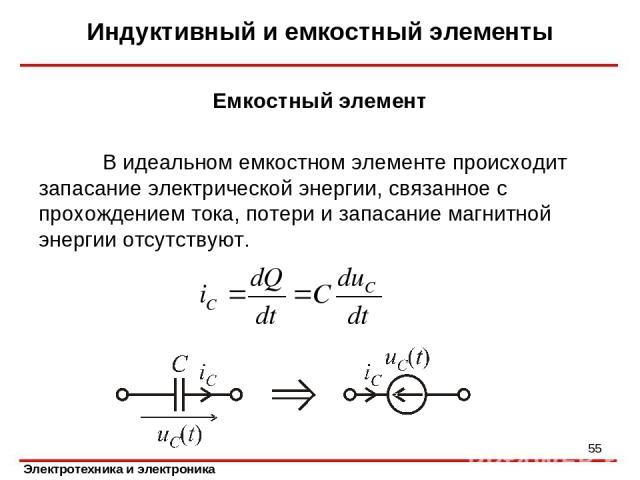
Индуктивный и емкостный элементы Емкостный элемент В идеальном емкостном элементе происходит запасание электрической энергии, связанное с прохождением тока, потери и запасание магнитной энергии отсутствуют. *

Законы коммутации и начальные условия Законы коммутации В начальный момент после коммутации токи индуктивных и напряжения емкостных элементов остаются такими же, какими они были перед коммутацией, а затем плавно изменяются. *

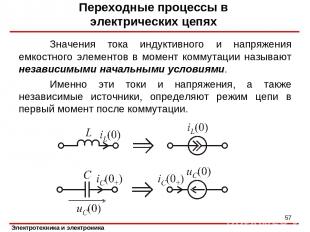
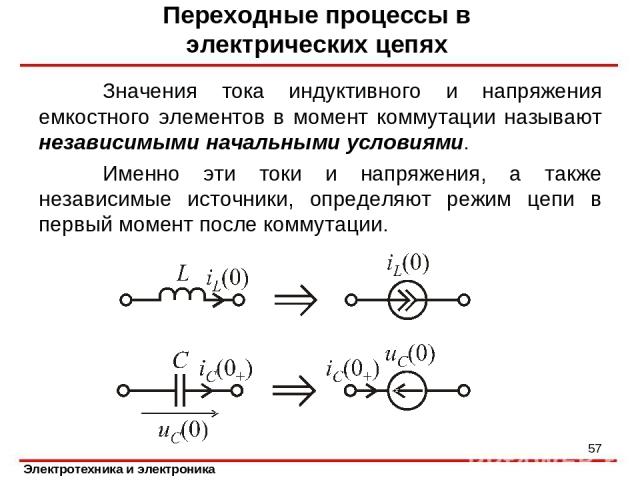
Значения тока индуктивного и напряжения емкостного элементов в момент коммутации называют независимыми начальными условиями. Именно эти токи и напряжения, а также независимые источники, определяют режим цепи в первый момент после коммутации. Переходные процессы в электрических цепях *

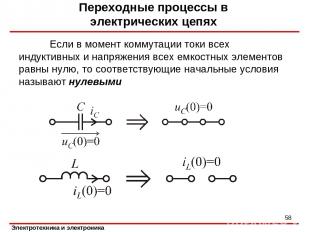
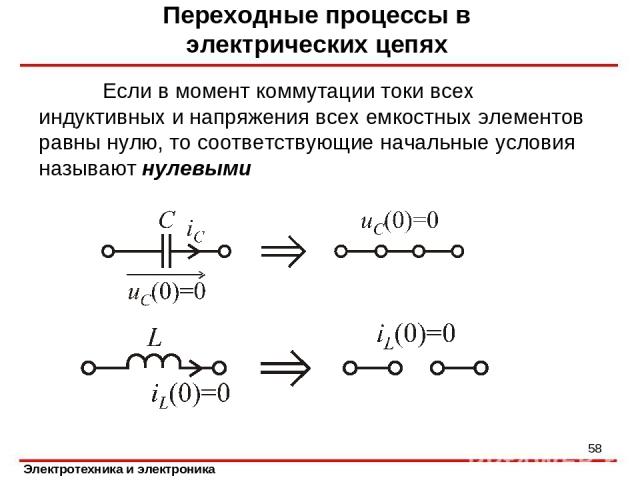
Если в момент коммутации токи всех индуктивных и напряжения всех емкостных элементов равны нулю, то соответствующие начальные условия называют нулевыми Переходные процессы в электрических цепях *

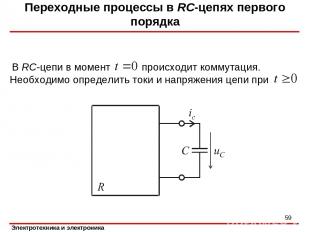
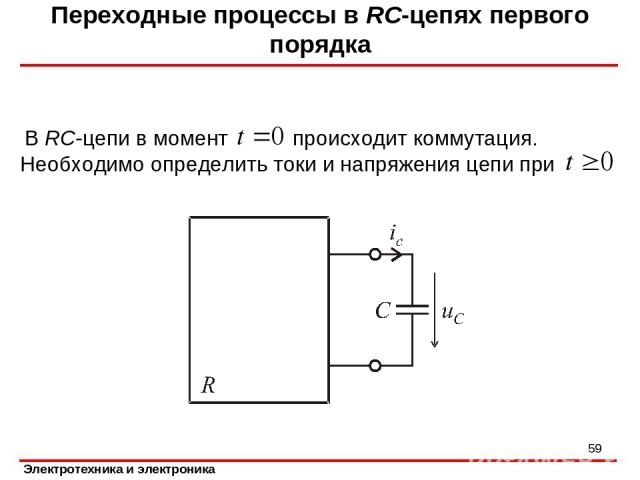
Переходные процессы в RC-цепях первого порядка *

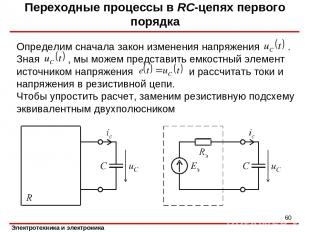
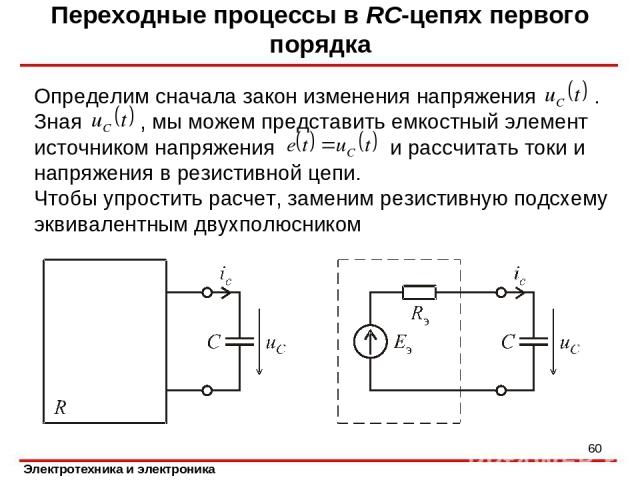
Переходные процессы в RC-цепях первого порядка Определим сначала закон изменения напряжения . Зная , мы можем представить емкостный элемент источником напряжения и рассчитать токи и напряжения в резистивной цепи. Чтобы упростить расчет, заменим резистивную подсхему эквивалентным двухполюсником *

Выполняя подстановку и решая полученное уравнение относительно , получим Переходные процессы в RC-цепях первого порядка - постоянная времени. (1) (2) * В соответствии со вторым законом Кирхгофа:

Первое слагаемое в (3) - свободная составляющая Второе слагаемое в (3) - принужденная (установившаяся) составляющая Переходные процессы в RC-цепях первого порядка (3) *

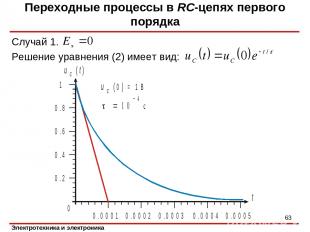
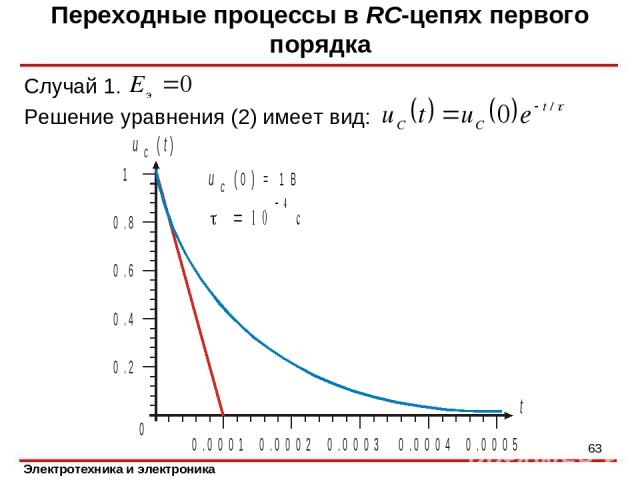
Случай 1. Решение уравнения (2) имеет вид: Переходные процессы в RC-цепях первого порядка *

Случай 2. Переходные процессы в RC-цепях первого порядка * Решение: Поскольку Запишем уравнение (2) в виде:

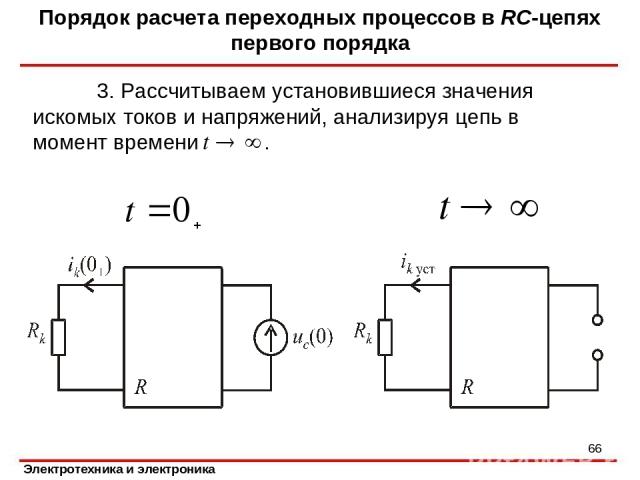
Порядок расчета переходных процессов в RC-цепях первого порядка Считаем, что переходный процесс вызван замыканием или размыканием идеального ключа в момент t = 0 и нужно определить ток k-й ветви. 1. Анализируем цепь в момент, предшествующий коммутации (при t = 0-), и определяем напряжение емкостного элемента UC (0). 2. Заменяем емкостный элемент источником напряжения E = UC (0) (рис. а). Анализируя полученную резистивную схему замещения, находим начальные значения искомых токов и напряжений *

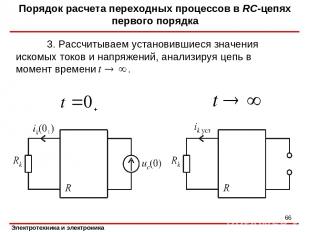
3. Рассчитываем установившиеся значения искомых токов и напряжений, анализируя цепь в момент времени . Порядок расчета переходных процессов в RC-цепях первого порядка *

4. Определяем входное сопротивление резистивной цепи со стороны зажимов, к которым подключен емкостный элемент. Рассчитываем постоянную времени цепи по формуле 5. Решение записываем в виде Важно! Все переходные токи и напряжения имеют одинаковую постоянную времени. Порядок расчета переходных процессов в RC-цепях первого порядка. *

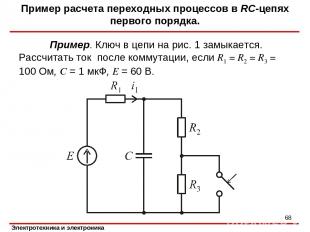
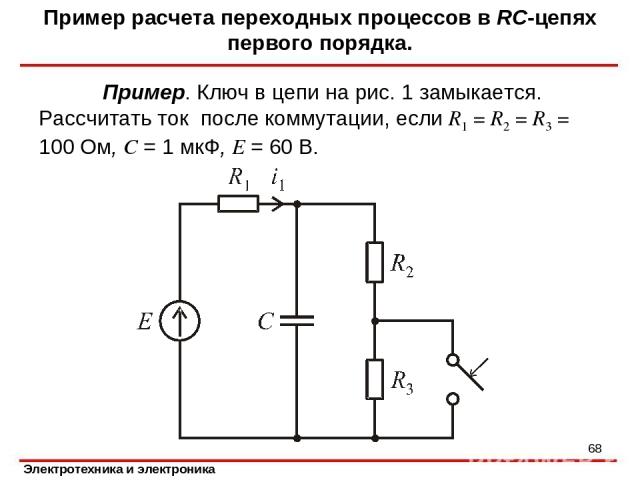
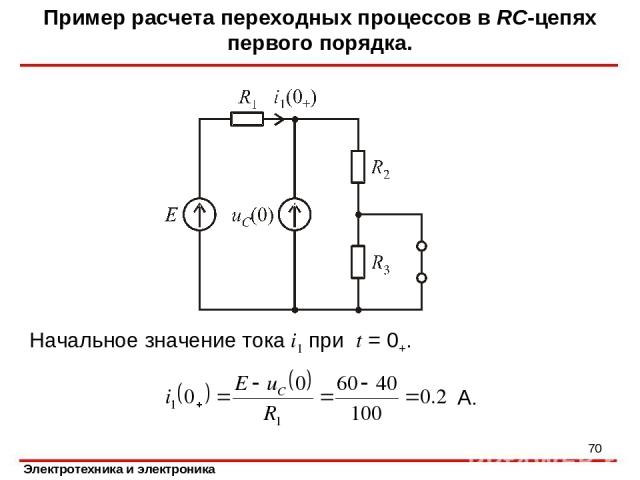
Пример. Ключ в цепи на рис. 1 замыкается. Рассчитать ток после коммутации, если R1 = R2 = R3 = 100 Ом, C = 1 мкФ, E = 60 В. Пример расчета переходных процессов в RC-цепях первого порядка. *

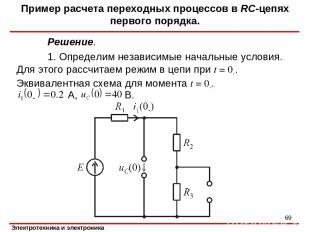
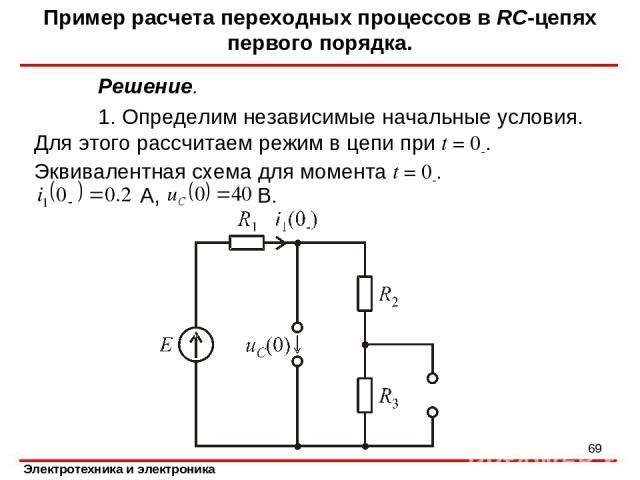
Решение. 1. Определим независимые начальные условия. Для этого рассчитаем режим в цепи при t = 0-. Эквивалентная схема для момента t = 0-. А, В. Пример расчета переходных процессов в RC-цепях первого порядка. *

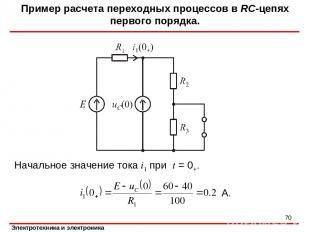
Начальное значение тока i1 при t = 0+. Пример расчета переходных процессов в RC-цепях первого порядка. А. *

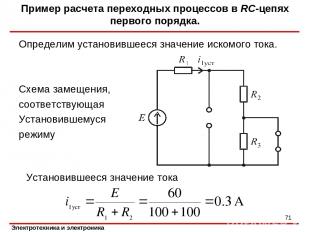
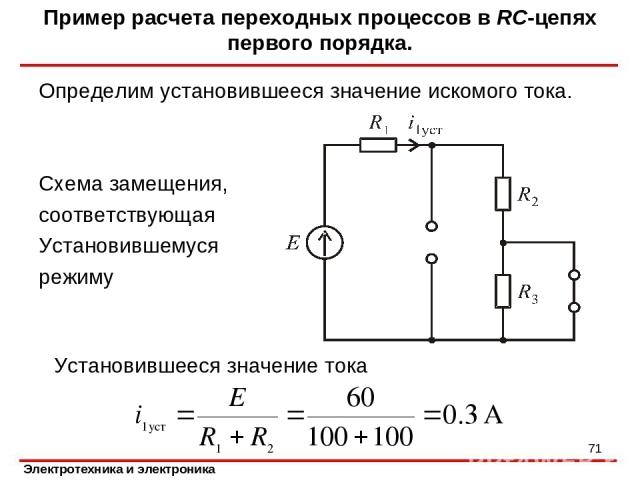
Определим установившееся значение искомого тока. Схема замещения, соответствующая Установившемуся режиму Установившееся значение тока Пример расчета переходных процессов в RC-цепях первого порядка. *

Определим входное сопротивление схемы относительно зажимов, к которым подключен емкостный элемент. Исключая источник напряжения, найдем, что Пример расчета переходных процессов в RC-цепях первого порядка. Постоянная времени цепи Закон изменения тока *

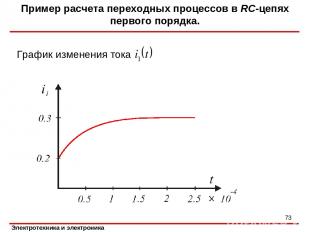
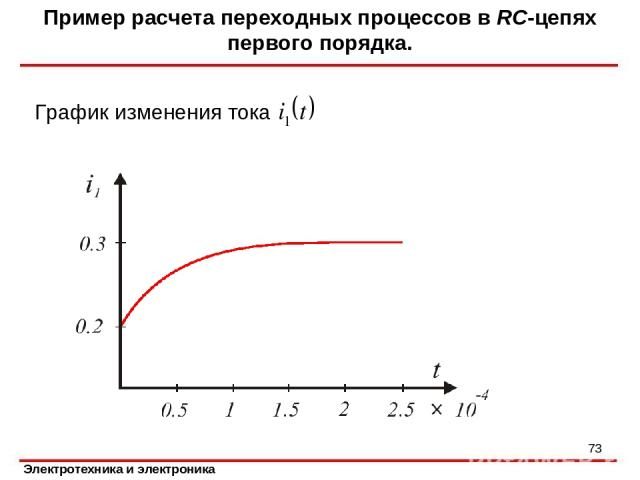
Пример расчета переходных процессов в RC-цепях первого порядка. График изменения тока *

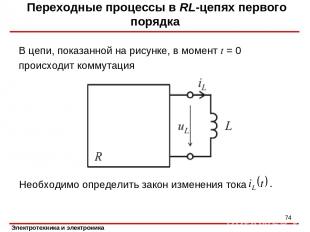
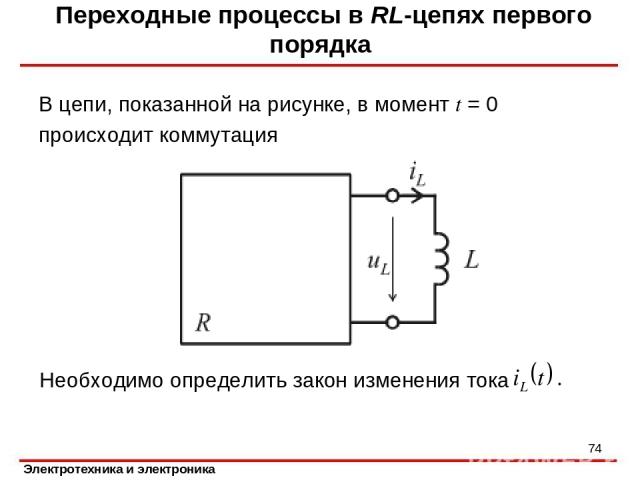
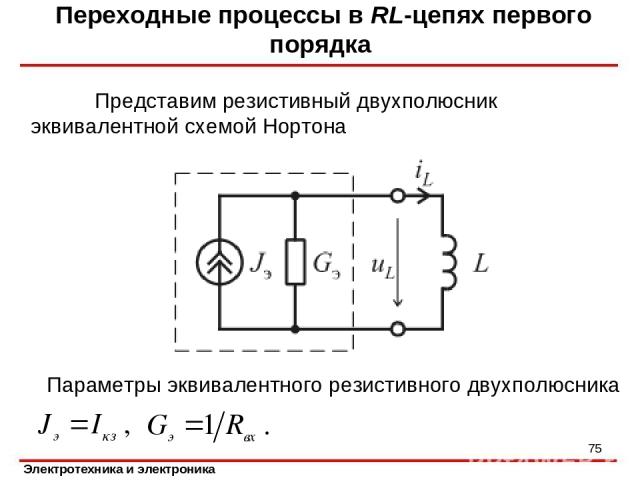
Переходные процессы в RL-цепях первого порядка В цепи, показанной на рисунке, в момент t = 0 происходит коммутация Необходимо определить закон изменения тока *

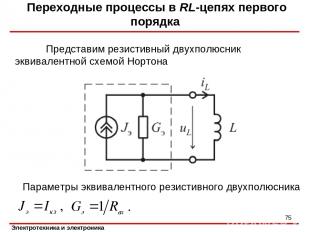
Представим резистивный двухполюсник эквивалентной схемой Нортона Переходные процессы в RL-цепях первого порядка Параметры эквивалентного резистивного двухполюсника *

Переходные процессы в RL-цепях первого порядка Уравнение по первому закону Кирхгофа: Учитывая, что , запишем уравнение состояния: (1) *

Решение уравнения (2) можно представить в следующем виде: Переходные процессы в RL-цепях первого порядка * (2) называют постоянной времени.

Порядок расчета переходных процессов в RL-цепях первого порядка. Переходный процесс вызван замыканием или размыканием идеального ключа в момент t = 0. 1. Анализируем цепь в момент, предшествующий коммутации (при t = 0-), и определяем ток индуктивного элемента iL(0). 2. Заменяем индуктивный элемент источником тока iL(0). Анализируя полученную схему замещения, определим начальные значения искомых напряжений или токов . Переходные процессы в RL-цепях первого порядка *

Переходные процессы в RL-цепях первого порядка 3. Замыкаем накоротко зажимы, к которым подключен индуктивный элемент. Определяем установившиеся значения интересующих нас токов и напряжений . 4. Определяем входное сопротивление резистивной цепи со стороны зажимов, к которым подключен индуктивный элемент. Рассчитываем постоянную времени цепи по формуле или . 5. Записываем решение в виде *

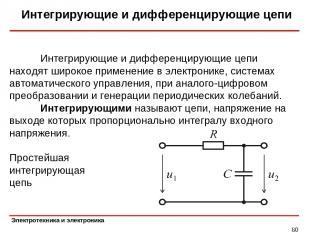
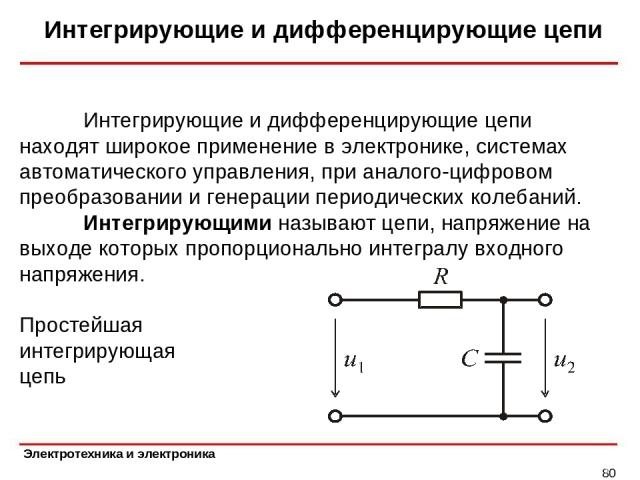
Интегрирующие и дифференцирующие цепи * Интегрирующие и дифференцирующие цепи находят широкое применение в электронике, системах автоматического управления, при аналого-цифровом преобразовании и генерации периодических колебаний. Интегрирующими называют цепи, напряжение на выходе которых пропорционально интегралу входного напряжения. Простейшая интегрирующая цепь

Интегрирующие и дифференцирующие цепи * Выходное напряжение Ток в цепи При выполнении условия за счет большого значения постоянной времени

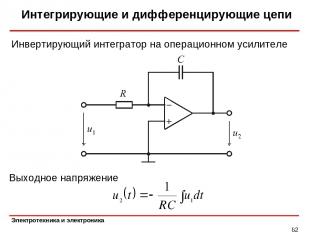
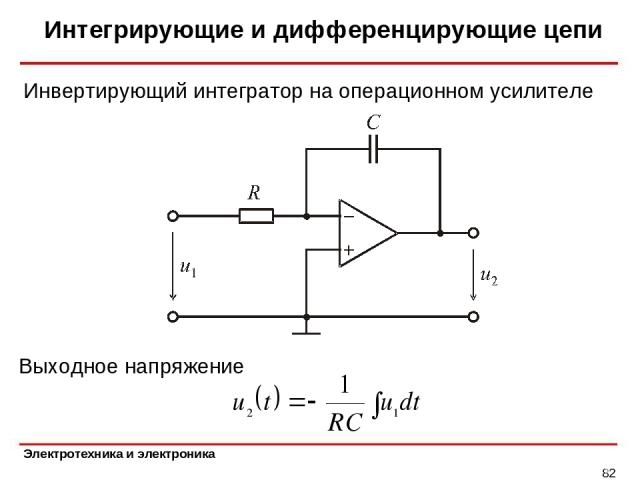
Интегрирующие и дифференцирующие цепи * Выходное напряжение Инвертирующий интегратор на операционном усилителе

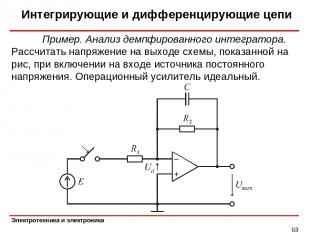
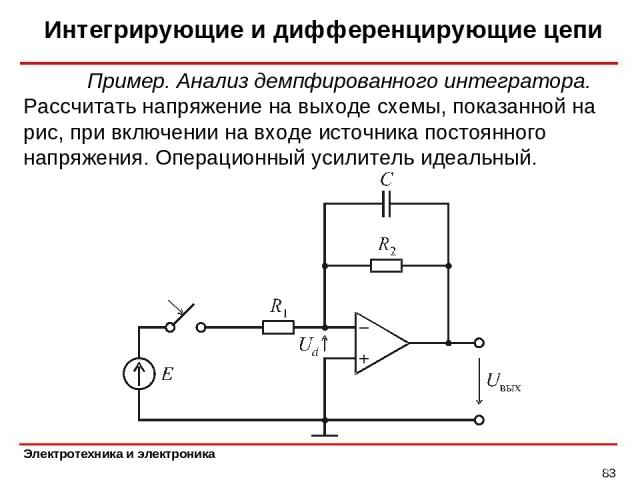
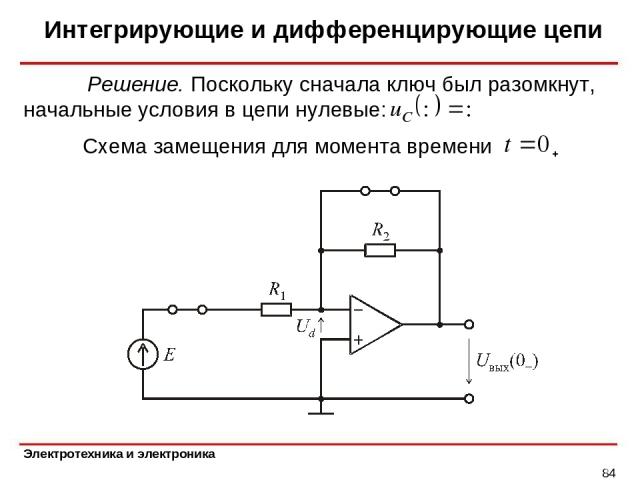
Интегрирующие и дифференцирующие цепи * Пример. Анализ демпфированного интегратора. Рассчитать напряжение на выходе схемы, показанной на рис, при включении на входе источника постоянного напряжения. Операционный усилитель идеальный.

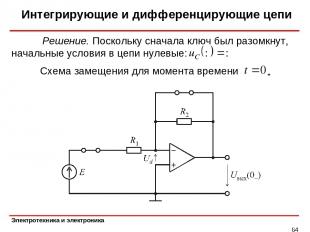
Интегрирующие и дифференцирующие цепи * Схема замещения для момента времени Решение. Поскольку сначала ключ был разомкнут, начальные условия в цепи нулевые:

Интегрирующие и дифференцирующие цепи * Поскольку , то Из уравнения по второму закону Кирхгофа для контура, включающего вход ОУ, емкостный элемент и выход схемы:

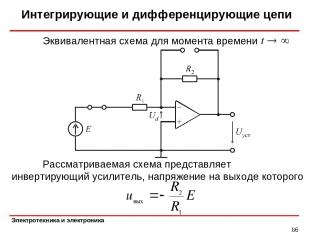
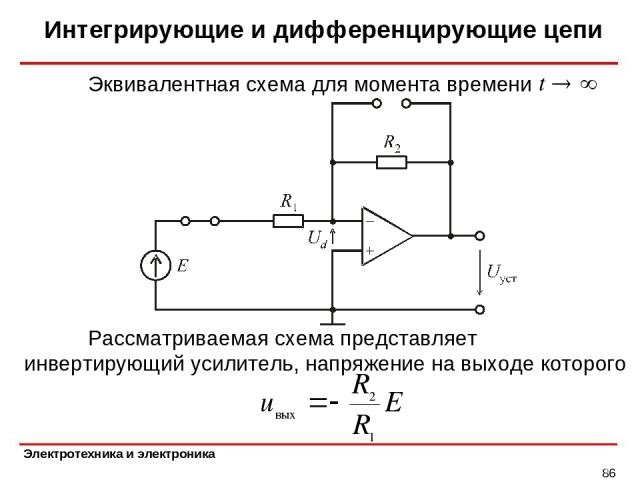
Интегрирующие и дифференцирующие цепи * Эквивалентная схема для момента времени Рассматриваемая схема представляет инвертирующий усилитель, напряжение на выходе которого

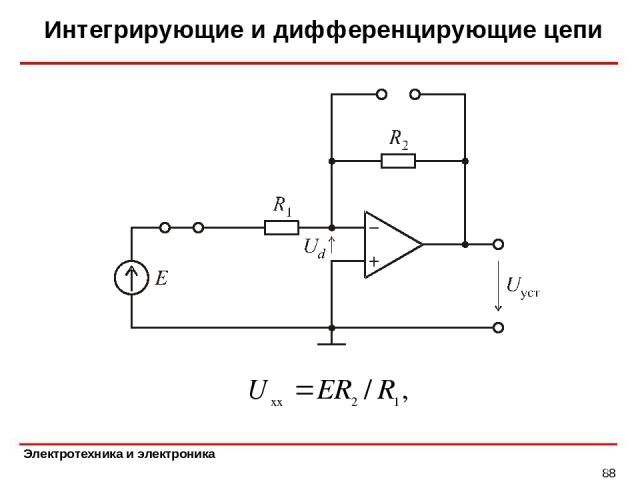
Интегрирующие и дифференцирующие цепи * Входное сопротивление резистивной части цепи относительно зажимов, к которым подключен емкостный элемент найдем как отношение напряжения холостого хода к току короткого замыкания:

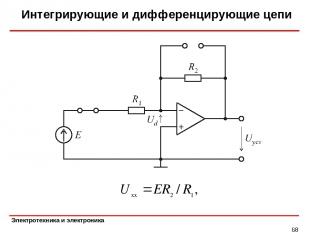
Интегрирующие и дифференцирующие цепи *

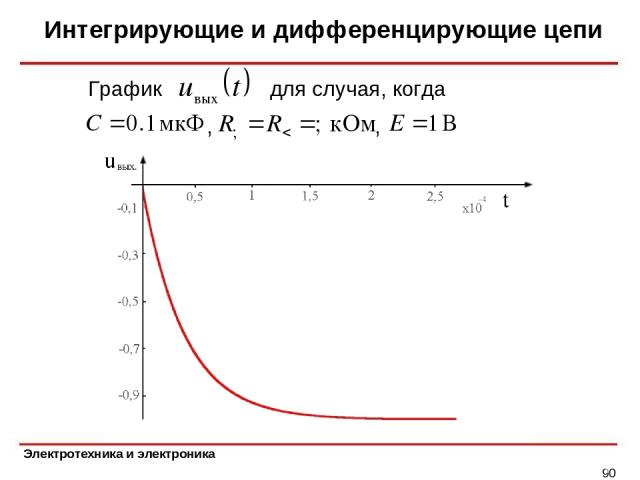
Интегрирующие и дифференцирующие цепи * Ток короткого замыкания Таким образом, Постоянная времени цепи Итак, напряжение на выходе интегратора изменяется по закону

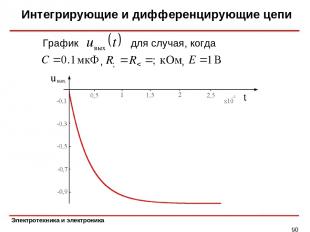
Интегрирующие и дифференцирующие цепи * График для случая, когда , ,

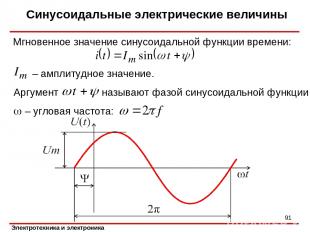
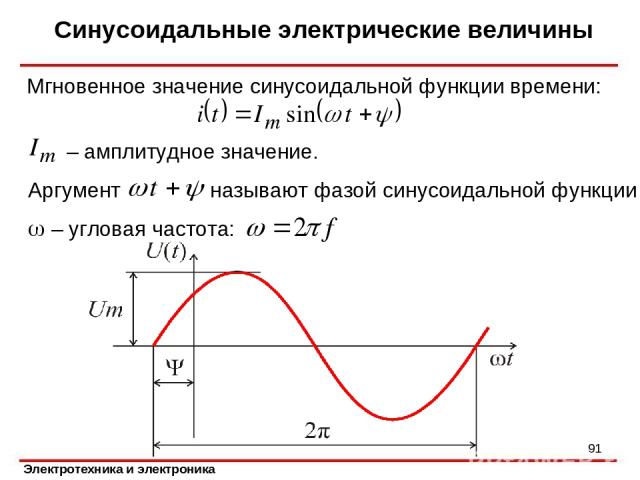
Синусоидальные электрические величины * – амплитудное значение. Аргумент называют фазой синусоидальной функции. Мгновенное значение синусоидальной функции времени: – угловая частота:

Синусоидальные электрические величины * О величине переменного тока судят по его среднему или действующему значению. Среднее значение периодической функции времени определяют по формуле:

Синусоидальные электрические величины * Среднее значение синусоидальной функции за период равно нулю. Поэтому используют понятие среднего значения за половину периода: Среднее значение синусоидального тока за половину периода

Синусоидальные электрические величины * Действующее значение синусоидального тока: Действующее значение переменного тока определяется по формуле:

Синусоидальные электрические величины * За один период переменного тока в резисторе сопротивлением R выделяется тепловая энергия, равная Действующее значение синусоидального тока равно такому постоянному току, при котором в резисторе за период выделяется такое же количество тепла, что и при переменном.

Резистивный элемент на синусоидальном токе * Пусть ток резистивного элемента изменяется синусоидально В соответствии с законом Ома напряжение Напряжение резистивного элемента изменяется синусоидально, причем начальные фазы напряжения и тока одинаковы. Ток и напряжение резистивного элемента совпадают по фазе.

Резистивный элемент на синусоидальном токе * Мгновенная мощность, поглощаемая резистивным элементом, равна: Мгновенная мощность резистивного элемента – пульсирующая функция времени.

Резистивный элемент на синусоидальном токе *

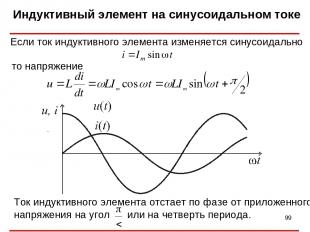
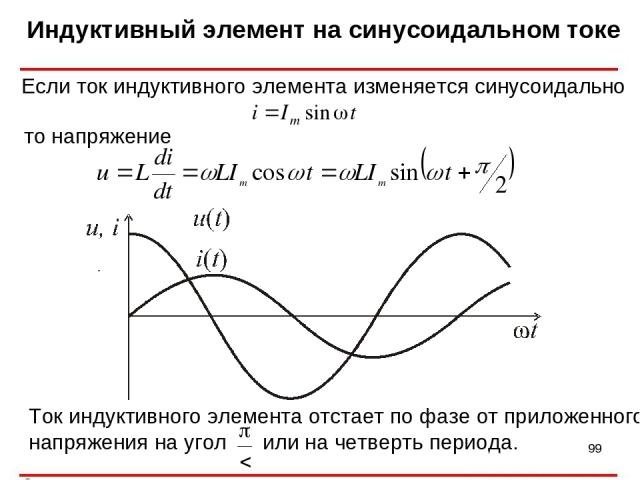
Индуктивный элемент на синусоидальном токе * Если ток индуктивного элемента изменяется синусоидально то напряжение Ток индуктивного элемента отстает по фазе от приложенного напряжения на угол или на четверть периода. .

Индуктивный элемент на синусоидальном токе * Амплитуда напряжения индуктивного элемента Величину , имеющую размерность сопротивления, называют индуктивным сопротивлением. Индуктивное сопротивление является линейной функцией частоты . .

Индуктивный элемент на синусоидальном токе * Мгновенная мощность индуктивного элемента Энергия, запасаемая в магнитном поле индуктивного элемента в первую четверть периода, во вторую четверть периода возвращается во внешнюю цепь. . Активная мощность индуктивного элемента равна нулю:

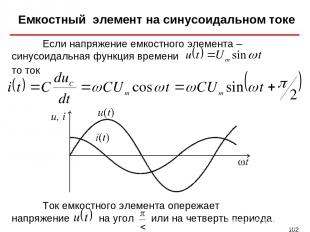
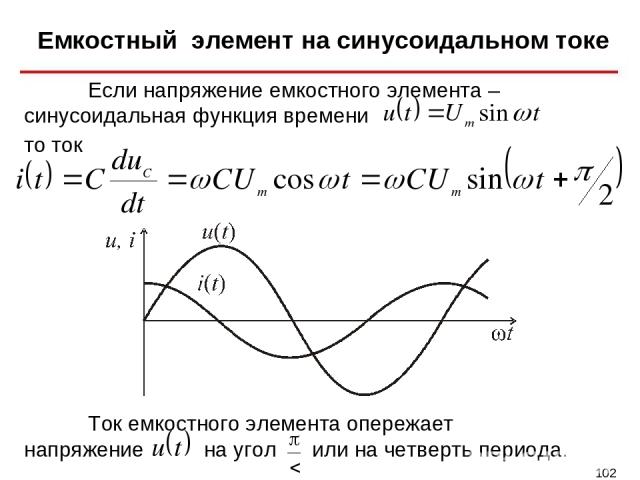
Емкостный элемент на синусоидальном токе * Если напряжение емкостного элемента – синусоидальная функция времени Ток емкостного элемента опережает напряжение на угол или на четверть периода. то ток

Емкостный элемент на синусоидальном токе * Амплитуда тока емкостного элемента Емкостное сопротивление обратно пропорционально частоте приложенного напряжения. Величина – емкостная проводимость. Величина, обратная емкостной проводимости, – емкостное сопротивление:

Емкостный элемент на синусоидальном токе * Мгновенная мощность емкостного элемента Активная мощность емкостного элемента равна нулю: Энергия, запасаемая в электрическом поле емкостного элемента в первую четверть периода, во вторую четверть периода возвращается во внешнюю цепь.

Резонанс и его значение в радиоэлектронике * При резонансе приложенное напряжение и входной ток совпадают по фазе. Цепи, в которых возникает явление резонанса, называют резонансными цепями или колебательными контурами. Резонанс – такой режим цепи синусоидального тока, содержащей индуктивные и емкостные элементы, при котором реактивное сопротивление и проводимость равны нулю.

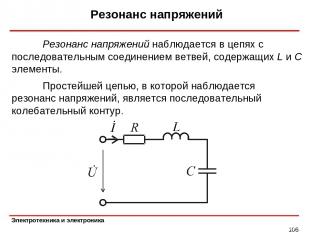
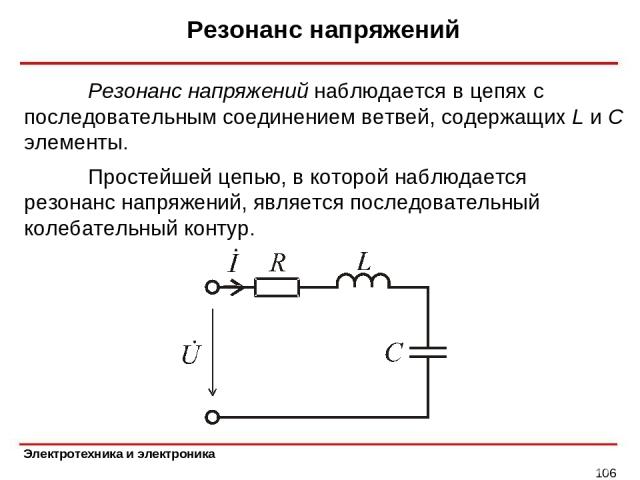
Резонанс напряжений * Простейшей цепью, в которой наблюдается резонанс напряжений, является последовательный колебательный контур. Резонанс напряжений наблюдается в цепях с последовательным соединением ветвей, содержащих L и C элементы.

Резонанс напряжений * Резонанс напряжений наступает, когда реактивное сопротивление обращается в нуль, т. е. Комплексное сопротивление последовательного колебательного контура Это происходит при резонансной частоте

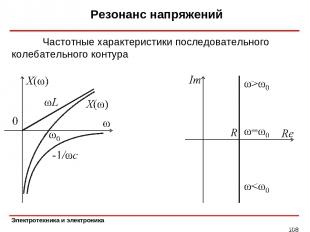
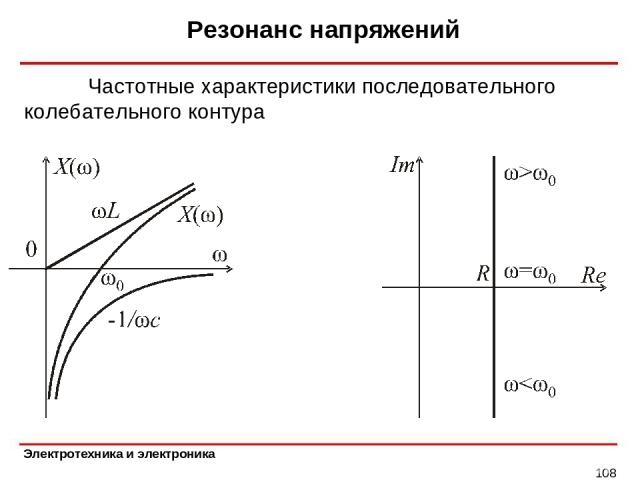
Резонанс напряжений * Частотные характеристики последовательного колебательного контура

Резонанс напряжений *

Резонанс напряжений *

Резонанс напряжений *

Резонанс напряжений * Величину называют добротностью колебательного контура. Добротность равна отношению напряжения на индуктивном и емкостном элементах в режиме резонанса к напряжению, приложенному к контуру.

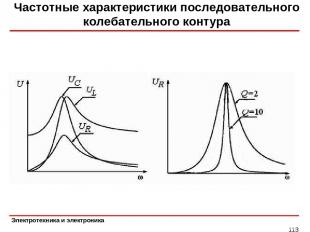
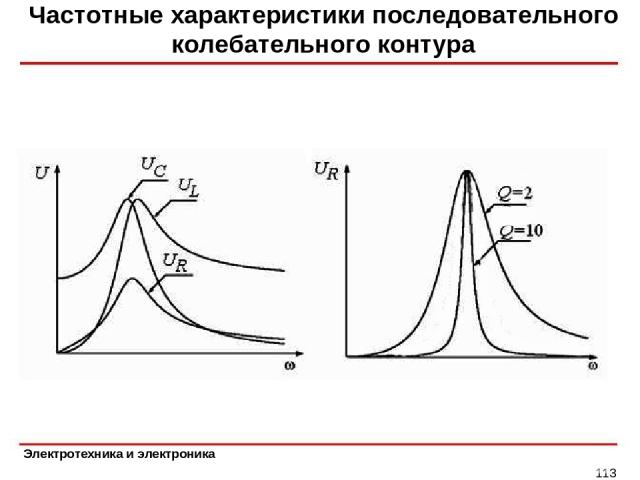
Частотные характеристики последовательного колебательного контура *

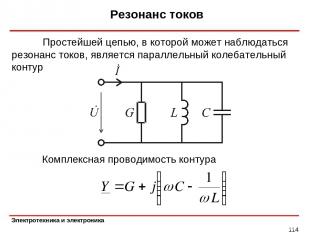
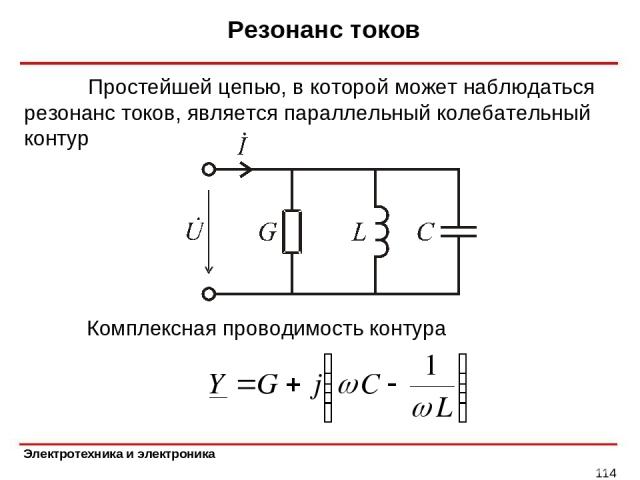
Резонанс токов * Простейшей цепью, в которой может наблюдаться резонанс токов, является параллельный колебательный контур Комплексная проводимость контура

Резонанс токов * Резонанс токов наступает, когда реактивная проводимость обращается в нуль: На резонансной частоте полная проводимость контура минимальна: Резонансная частота

Резонанс токов * Полное сопротивление параллельного колебательного контура на частоте резонанса максимально

Резонанс токов * Следовательно, при резонансе токов ток неразветвленной части цепи имеет наименьшее значение и равен току резистивного элемента: При резонансе токи емкостного и индуктивного элементов

Резонанс токов * Величину называют добротностью параллельного колебательного контура. Как и в случае последовательного колебательного контура, характеристическое сопротивление Добротность параллельного колебательного контура тем больше, чем больше сопротивление резистора R, включенного параллельно индуктивному и емкостному элементам.

Ряд Фурье в тригонометрической форме * Ряд Фурье в тригонометрической форме

Ряд Фурье в тригонометрической форме * Коэффициенты an и bn вычисляются по формулам – постоянная составляющая, равная среднему значению функции f(t) за период:

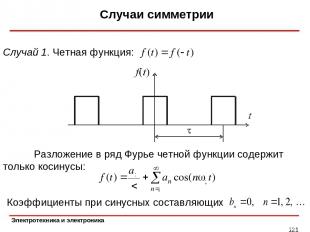
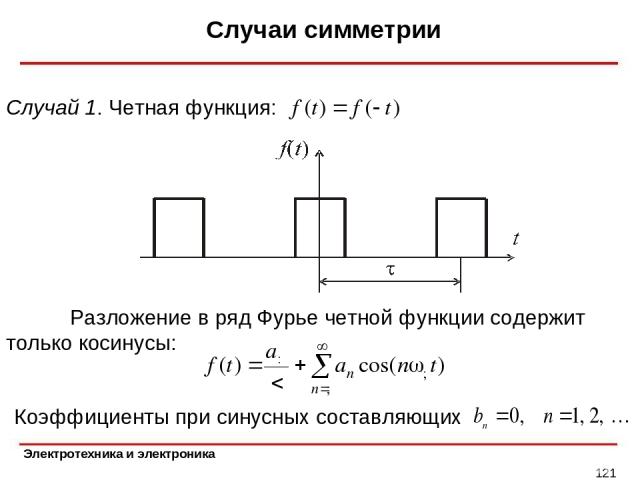
Случаи симметрии * Случай 1. Четная функция: Разложение в ряд Фурье четной функции содержит только косинусы: Коэффициенты при синусных составляющих

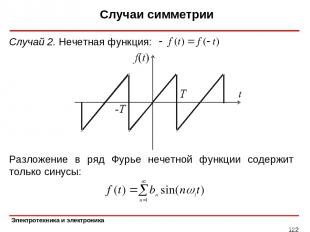
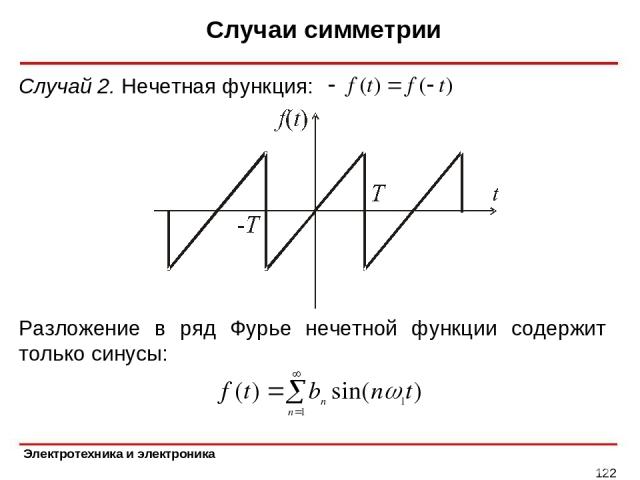
Случаи симметрии * Случай 2. Нечетная функция: Разложение в ряд Фурье нечетной функции содержит только синусы:

Случаи симметрии * Случай 3. Функция f(t) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени, т. е. Четные гармоники, а также составляющая равны нулю, т. е.

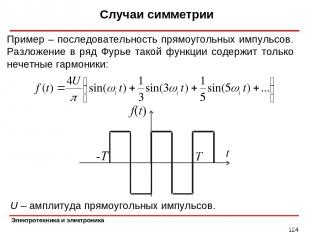
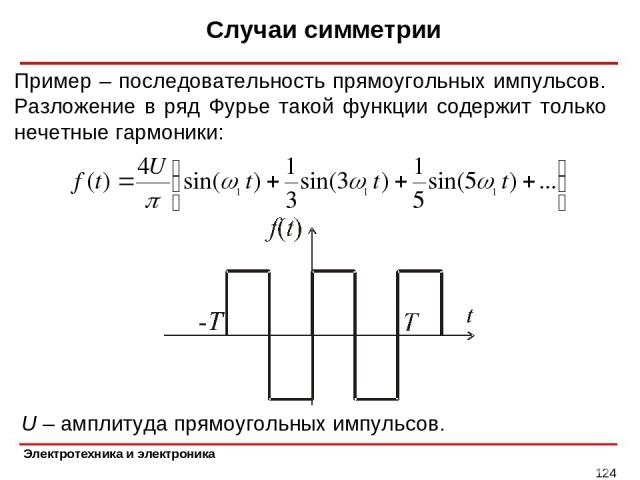
Случаи симметрии * Пример – последовательность прямоугольных импульсов. Разложение в ряд Фурье такой функции содержит только нечетные гармоники: U – амплитуда прямоугольных импульсов.

Комплексная форма ряда Фурье * Ряд Фурье в тригонометрической форме Воспользуемся равенствами:

Комплексная форма ряда Фурье * Ряд Фурье примет вид: Коэффициент an – четная, а bn – нечетная функция индекса n: Поэтому элемент -jbn можно рассматривать как слагаемое с отрицательным индексом. ,

Комплексная форма ряда Фурье * Изменив нижний предел суммирования на , получим – комплексный коэффициент ряда Фурье. В показательной форме: ,

Комплексный частотный спектр * Амплитуды гармоник образуют амплитудный спектр. Совокупность комплексных коэффициентов гармоник называют комплексным частотным спектром функции Начальные фазы образуют фазовый спектр.

Комплексный частотный спектр * Используя равенства Комплексная амплитуда n-й гармоники получим, что комплексный коэффициент ряда Фурье

Электрические свойства полупроводников Полупроводниками называют вещества, удельная проводимость которых имеет промежуточное значение между удельными проводимостями металлов и диэлектриков.   В отличие от металлов в полупроводниках носители заряда возникают при повышении температуры или поглощении энергии от другого источника.   Кроме того, в полупроводниках электропроводность осуществляется двумя различными видами движения электронов. Проводимость полупроводников можно менять в широких пределах, добавляя ничтожно малые количества примесей. *

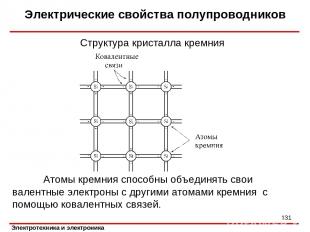
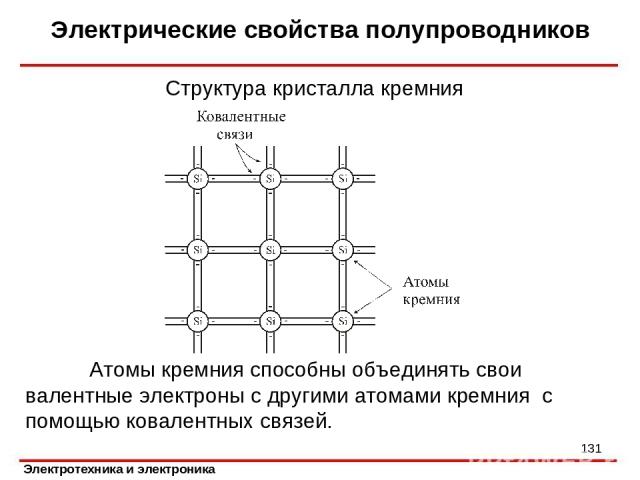
Электрические свойства полупроводников Структура кристалла кремния Атомы кремния способны объединять свои валентные электроны с другими атомами кремния с помощью ковалентных связей. *

Электрические свойства полупроводников При освобождении электрона в кристаллической решетке появляется незаполненная межатомная связь. Такие «пустые» места с отсутствующими электронами получили название дырок.   Возникновение дырок в кристалле полупроводника создает дополнительную возможность для переноса заряда. Дырка может быть заполнена электроном, перешедшим под действием тепловых колебаний от соседнего атома. Последовательное заполнение свободной связи электронами эквивалентно движению дырки в направлении, противоположном движению электронов, что равносильно перемещению положительного заряда. *

Электрические свойства полупроводников Таким образом, в полупроводнике имеются два типа носителей заряда – электроны и дырки, а общая проводимость полупроводника является суммой электронной проводимости (n-типа) и дырочной проводимости (р-типа). Для увеличения проводимости чистых полупроводниковых материалов применяют легирование – добавление небольших количеств посторонних элементов, называемых примесями.   Используются два типа примесей. Примеси первого типа – пятивалентные – состоят из атомов с пятью валентными электронами. Примеси второго типа – трехвалентные – состоят из атомов с тремя валентными электронами. *

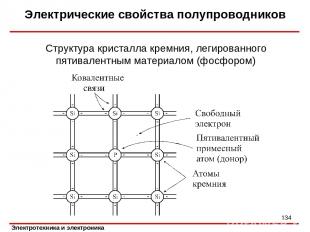
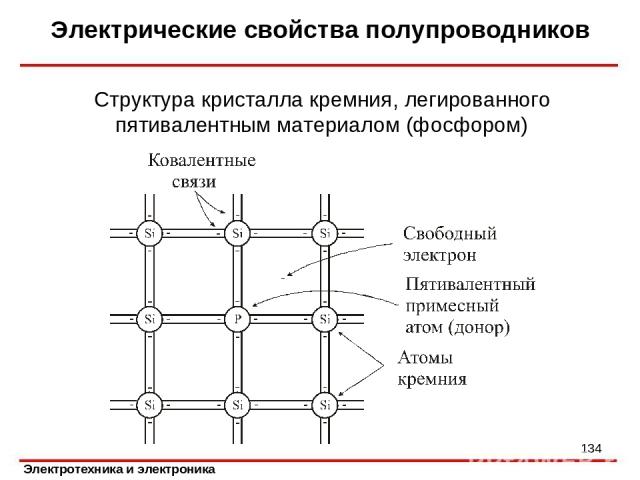
Электрические свойства полупроводников Структура кристалла кремния, легированного пятивалентным материалом (фосфором) *

Электрические свойства полупроводников Атом фосфора называют донором, поскольку он отдает свой лишний электрон. Электроны в таком полупроводнике являются основными носителями, а дырки – неосновными носителями. Основные носители имеют отрицательный заряд, поэтому такой материал называется полупроводником n-типа. В качестве донорных примесей для германия и кремния используют фосфор, мышьяк, сурьму. *

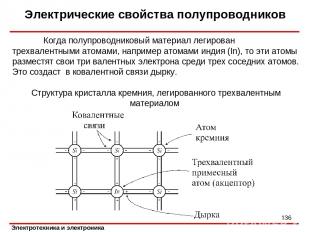
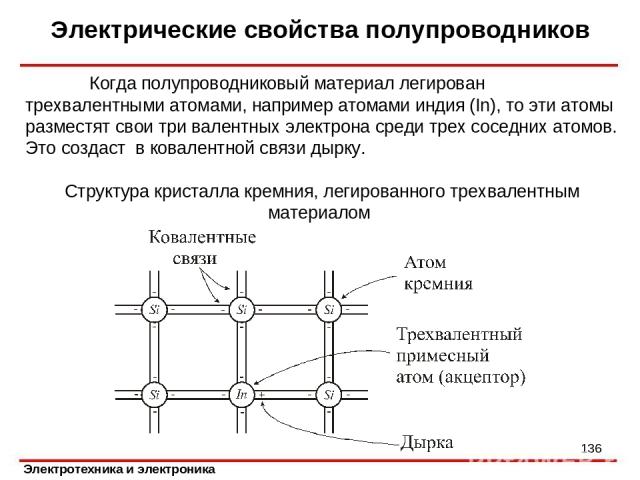
Электрические свойства полупроводников Когда полупроводниковый материал легирован трехвалентными атомами, например атомами индия (In), то эти атомы разместят свои три валентных электрона среди трех соседних атомов. Это создаст в ковалентной связи дырку. Структура кристалла кремния, легированного трехвалентным материалом *

Электрические свойства полупроводников Так как дырки легко принимают электроны, то атомы, которые вносят в полупроводник дополнительные дырки, называются акцепторами. Дырки являются основными носителями, а электроны – неосновными. Поскольку основные носители имеют положительный заряд, материал называется полупроводником р-типа.   В качестве акцепторных примесей в германии и кремнии используют бор, алюминий, галлий, индий. *

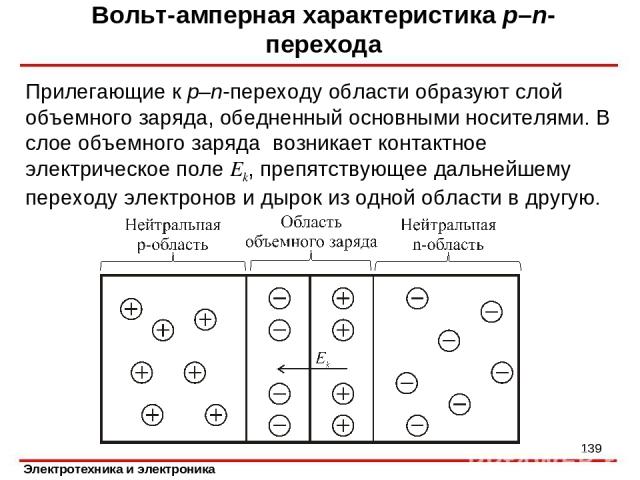
Вольт-амперная характеристика р–n-перехода Контакт двух полупроводников с различными типами проводимости называется р–n-переходом. Сопротивление р–n-перехода зависит от направления тока через него. Поскольку концентрация электронов в n-области значительно больше их концентрации в p-области, происходит диффузия электронов из n-области в p-область. В n-области остаются неподвижные положительно заряженные ионы доноров. Одновременно происходит диффузия дырок из p-области в n-область. За счет этого приграничная р-область приобретает отрицательный заряд, обусловленный отрицательно заряженными ионами акцепторов. *

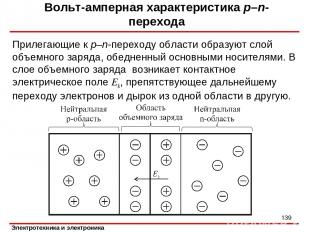
Вольт-амперная характеристика р–n-перехода Прилегающие к р–n-переходу области образуют слой объемного заряда, обедненный основными носителями. В слое объемного заряда возникает контактное электрическое поле Ek, препятствующее дальнейшему переходу электронов и дырок из одной области в другую. *