Презентация на тему: Динамика материальной системы

ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ ЛЕКЦИЯ 3: ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

1. Кинетическая энергия МС. Теорема Кенига Кинетической энергией материальной системы называется сумма кинетических энергий входящих в нее точекПри вычислении кинетической энергии системы полезна теорема КенигаТеорема Кинетическая энергия материальной системы в ее абсолютном движении (T) складывается из кинетической энергии TO центра масс, в предположении, что в нем сосредоточена масса всей системы, и кинетической энергии Tотн системы в ее движении относительно поступательно перемещающихся в инерциальном пространстве вместе с центром масс осей.

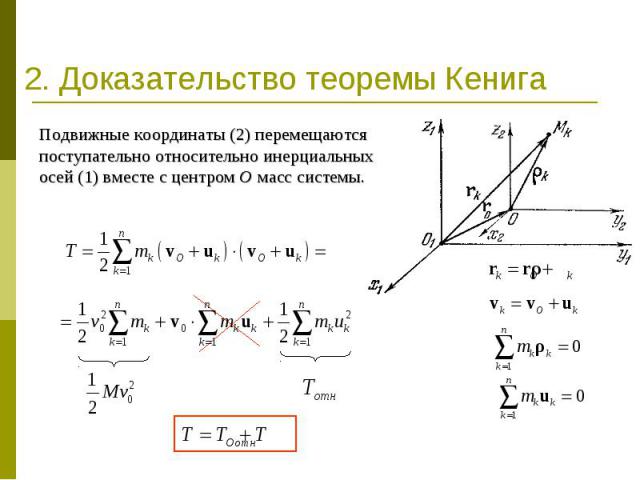
2. Доказательство теоремы Кенига Подвижные координаты (2) перемещаются поступательно относительно инерциальных осей (1) вместе с центром О масс системы.

3. Кинетическая энергия ТТ, движущегося поступательно кинетическая энергия ТТ, движущегося поступательно, равна половине произведения массы тела на квадрат его скорости

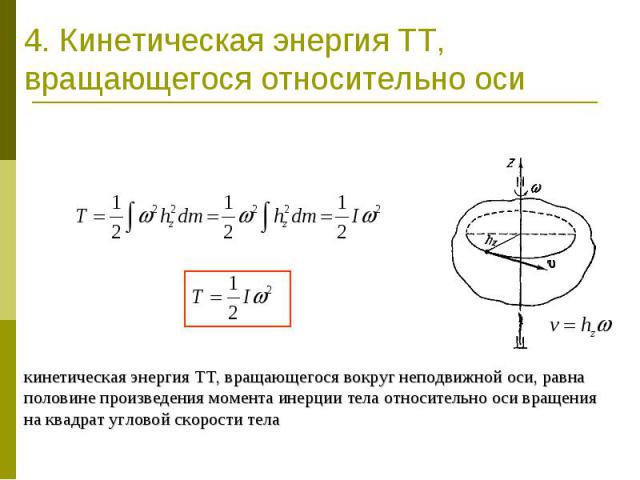
4. Кинетическая энергия ТТ, вращающегося относительно оси кинетическая энергия ТТ, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела

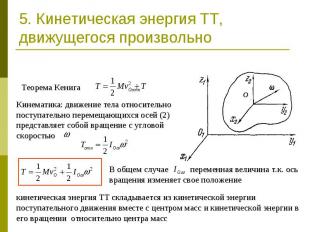
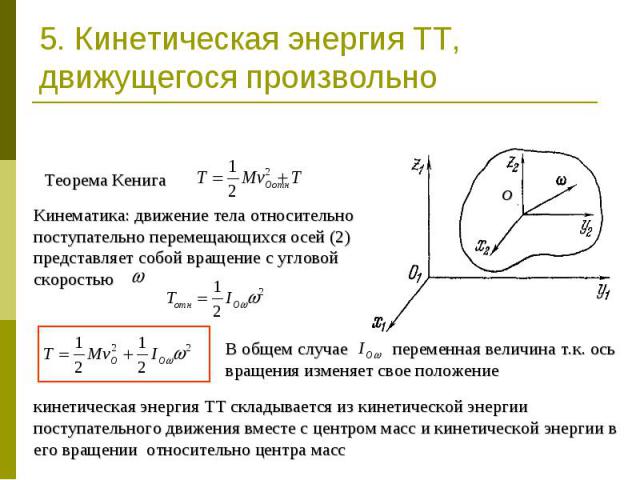
5. Кинетическая энергия ТТ, движущегося произвольно Теорема КенигаКинематика: движение тела относительно поступательно перемещающихся осей (2) представляет собой вращение с угловой скоростью В общем случае переменная величина т.к. ось вращения изменяет свое положениекинетическая энергия ТТ складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии в его вращении относительно центра масс

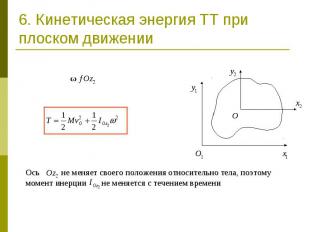
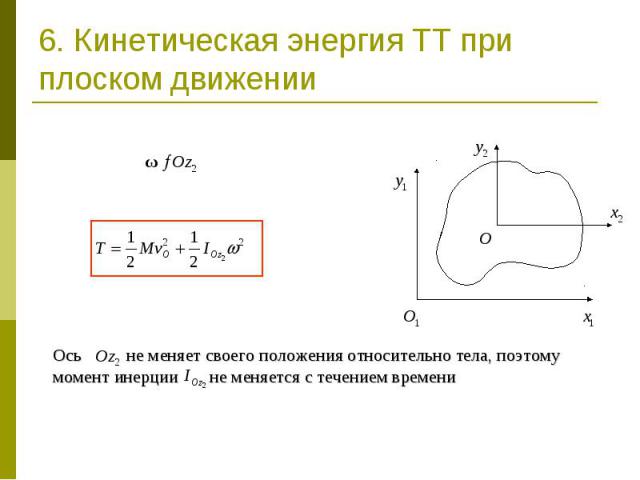
6. Кинетическая энергия ТТ при плоском движении Ось не меняет своего положения относительно тела, поэтому момент инерции не меняется с течением времени

7. Пример вычисления кинетической энергии Каток К массы m1 лежит на горизонтальной плос-кости. Каток обмотан тросом, перекинутым через блок Б радиуса r. К свободному концу троса при-креплен груз Г массы m3. При опускании груза со скоростью v трос, разматываясь, приводит в качение без скольжения каток. Определить кинетическую энергию системы, если момент инерции блока Б относительно оси вращения равен I2Скорость точки касания блока с тросом равна скорости v груза Г.

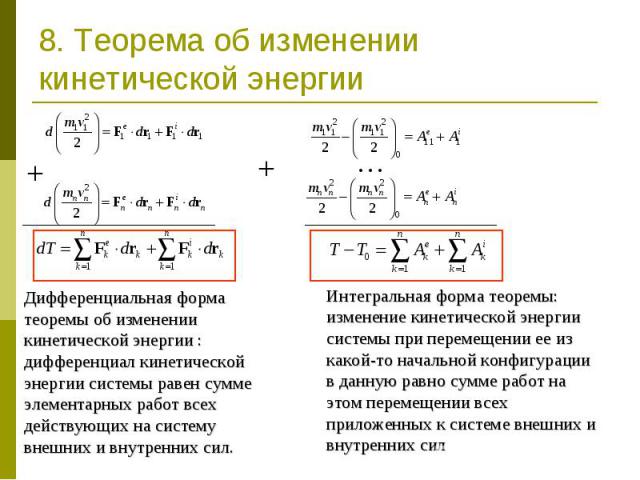
8. Теорема об изменении кинетической энергии Дифференциальная форма теоремы об изменении кинетической энергии : дифференциал кинетической энергии системы равен сумме элементарных работ всех действующих на систему внешних и внутренних сил. Интегральная форма теоремы: изменение кинетической энергии системы при перемещении ее из какой-то начальной конфигурации в данную равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил

9. Работа сил тяжести Полная работа сил тяжести системы равна весу всей системы, умноженному на вертикальное перемещение ее центра тяжести

10. Работа внутренних сил твердого тела КинематикаСумма работ всех внутренних сил абсолютно твердого тела на любом его перемещении равна нулю

11. Работа силы, приложенной к вращающемуся твердому телу Элементарная работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна моменту этой силы относительно оси вращения, умноженному на дифференциал угла поворота телаМощность:

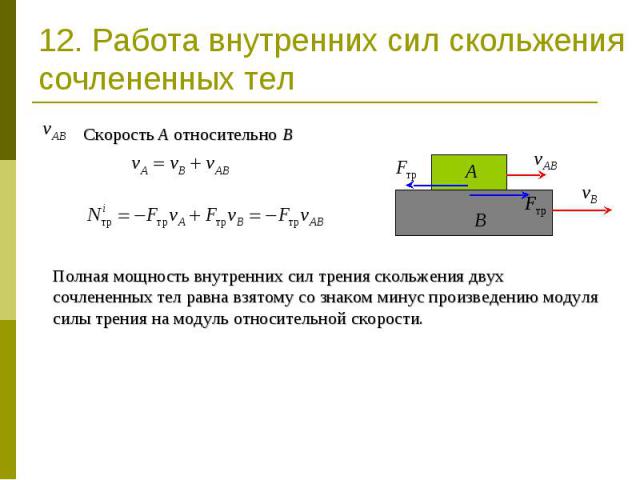
12. Работа внутренних сил скольжения сочлененных тел Скорость A относительно BПолная мощность внутренних сил трения скольжения двух сочлененных тел равна взятому со знаком минус произведению модуля силы трения на модуль относительной скорости.

13. Работа потенциальных внутренних сил Ui-потенциальная энергия внутренних сил (внутренняя энергия)

14. Работа потенциальных внешних сил На точку #1 действуют потенциальные внешние силыНа точку #2 действуют потенциальные внешние силыНа точку #n действуют потенциальные внешние силыUe-потенциальная энергия внешних сил

15. Закон сохранения полной механической энергии Допустим, что внутренние и внешние силы, работа которых отлична от нуля, потенциальны (нулю может равняться работа идеальных связей). Ue-потенциальная энергия внешних силUi-внутренняя энергияE-полная механическая энергия системыинтеграл энергииСистему, для которой имеет место интеграл энергии, называют консервативной.

16. Пример # 1 Цилиндр катится без скольжения по наклонной плоскости. Начальная скорость равна нулю. Найти скорость центра масс цилиндра в момент времени когда он опустился на величину h. Если это тело спускается не вращаясь, имеем Следовательно, вращение уменьшает скорость

17. Пример # 2 Груз Г под действием силы тяжести опускается из состояния покоя вниз. Определить скорость v груза Г при опускании его на высоту h. Трением качения катка и трением на оси блока пренебречь. Связи идеальны. Внутренняя энергия равна нулю

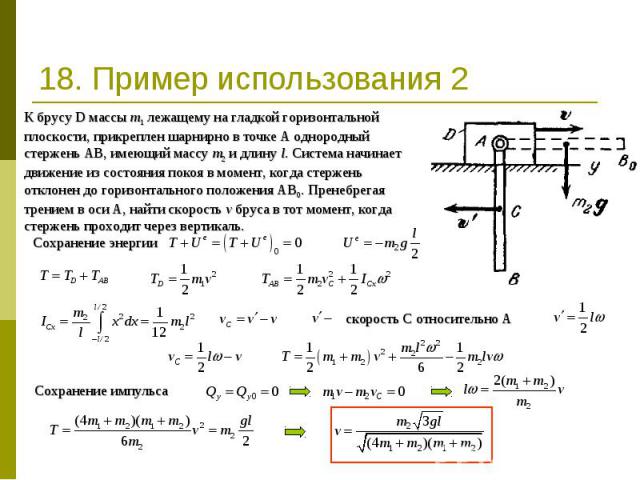
18. Пример использования 2 К брусу D массы m1 лежащему на гладкой горизонтальной плоскости, прикреплен шарнирно в точке А однородный стержень АВ, имеющий массу m2 и длину l. Система начинает движение из состояния покоя в момент, когда стержень отклонен до горизонтального положения АВ0. Пренебрегая трением в оси А, найти скорость v бруса в тот момент, когда стержень проходит через вертикаль. Сохранение энергиискорость С относительно АСохранение импульса

19. Основные теоремы и законы сохранения