Презентация на тему: Факторный анализ

Факторный анализ Методика факторного анализа Типы детерминированных факторных моделей Способы измерения влияния факторов в детерминированных факторных моделях Стохастические факторные модели Способы измерения влияния факторов в стохастическом факторном анализе

Стохастический факторный анализ Корреляционный метод Регрессионный метод Дисперсионный метод Метод кластерного анализа Другие методы

Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Целью корреляционного анализа является оценка тесноты связи между признаками. Теснота связи количественно выражается величиной коэффициентов корреляции.

Корреляционный анализ: 1. Парная корреляция – связь между двумя признаками (результативным и факторным или двумя факторными). 2. Частная корреляция – зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков. 3. Множественная корреляция – зависимость результативного и двух или более факторных признаков, включенных в исследование.

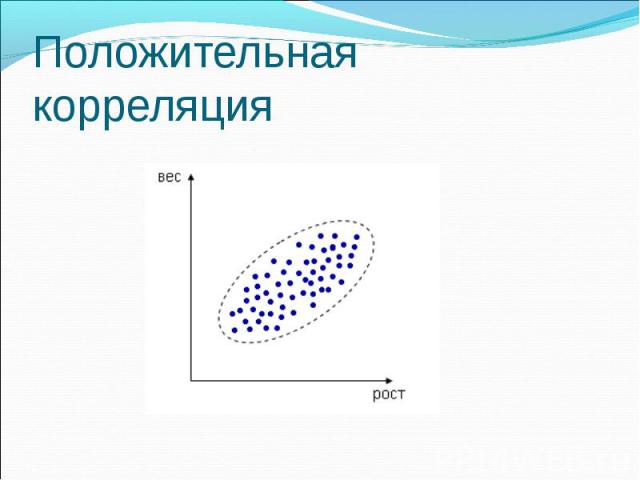
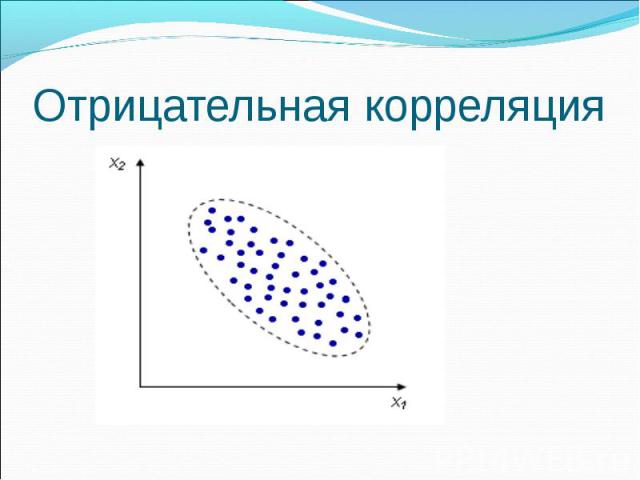
Виды корреляционных связей: По форме корреляционная связь может быть прямолинейной или криволинейной. По направлению корреляционная связь может быть положительной (\"прямой\") и отрицательной (\"обратной\"). По силе корреляционная связь определяется шкалой Чеддока

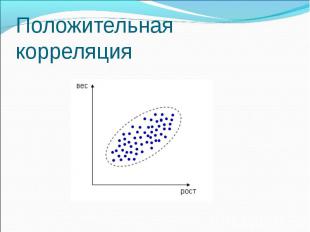
Положительная корреляция

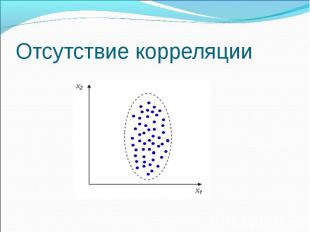
Отсутствие корреляции

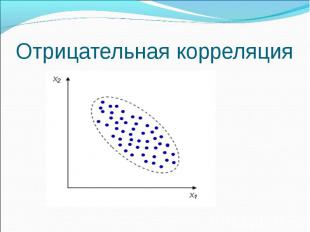
Отрицательная корреляция

Шкала Чеддока

Термин «корреляция» был введен в науку английским естествоиспытателем Френсисом Гальтоном в 1886 г. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон.

Формула коэффициента корреляции при линейной зависимости

Величина коэффициента линейной корреляции Пирсона не может превышать +1 и быть меньше чем -1. Эти два числа +1 и -1 — являются границами для коэффициента корреляции. Когда при расчете получается величина большая +1 или меньшая -1 — следовательно произошла ошибка в вычислениях.

Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами. Целью регрессионного анализа является установление формы зависимости.

Виды регрессий Линейная регрессия: у=а+bх Регрессии, нелинейные по объясняющим переменным: 1) полиномы разных степеней у=а+b1х+b2х2+…; 2) равносторонняя гипербола у=а+b/х. Регрессии, нелинейные по оцениваемым параметрам: 1) степенная у=ахb; 2) показательная у=аbх; 3) экспоненциальная у=еа+bх.

Оценки параметров a и b находятся по формулам:

Формально a – значение y при x =0. Если признак-фактор x не может иметь нулевого значения, то вышеуказанная трактовка свободного члена a не имеет смысла, т.е. параметр a может не иметь экономического содержания. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Коэффициент детерминации

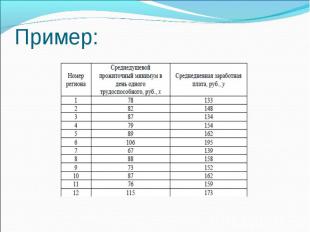
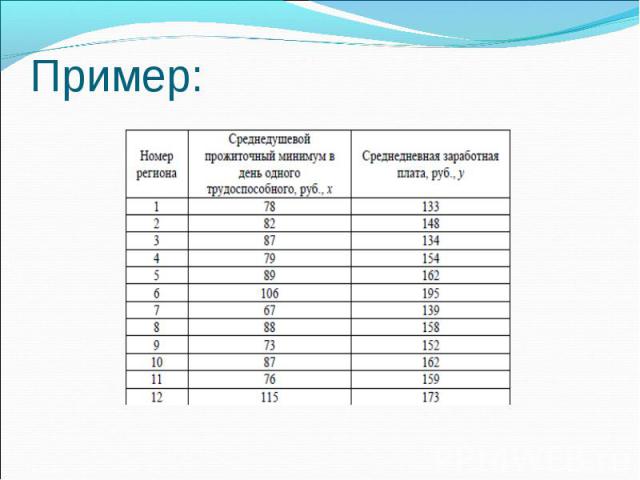
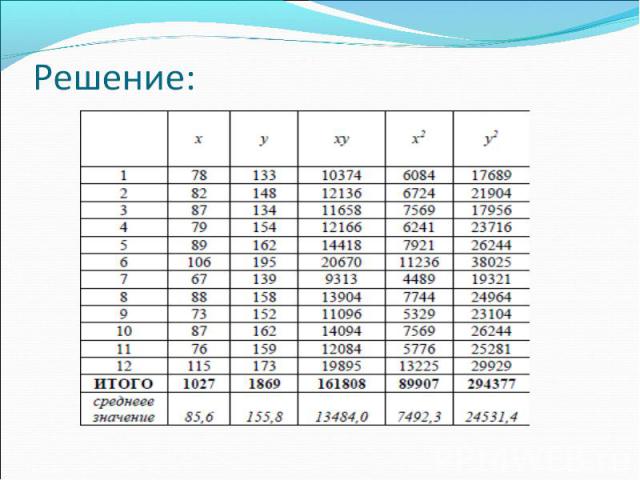
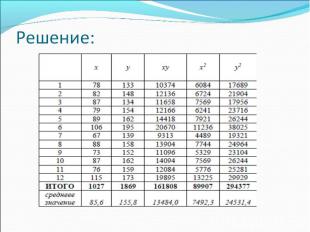
Пример:

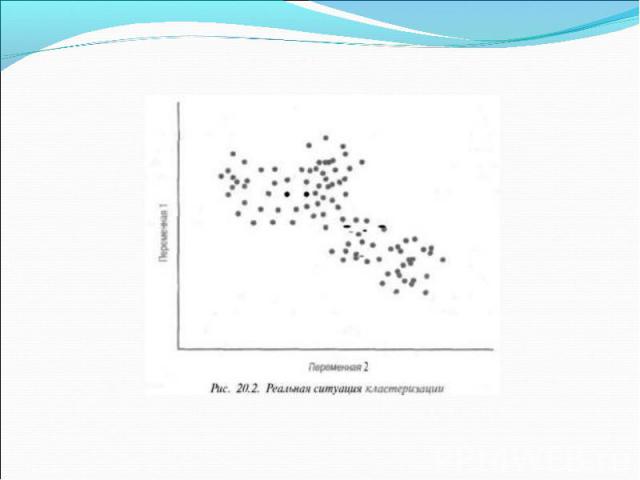
Кластерный анализ Кластерный анализ представляет собой класс методов, используемых для классификации объектов или событий в относительно однородные группы, которые называют кластерами (clusters).

Кластерный анализ Объекты в каждом кластере должны быть похожи между собой и отличаться от объектов в других кластерах. Кластерный анализ также называют классификационным анализом (classification analysis) или численной таксономией (систематикой) (numerical taxonomy).

Самостоятельная работа