Презентация на тему: Продолжительность жизни

Продолжительность жизни животных в единицах физического и биологического времени А.Ф. Алимов, Т.И. Казанцева Зоологический институт РАН 900igr.net

При рассмотрении понятия времени применительно к живым организмам возникают три главных вопроса: Какова максимально возможная продолжительность жизни организма? Что такое биологическое (внутреннее) время организма и как оно соотносится с физическим (внешним) временем? Как эти величины связаны с массой организма?

Мы попытались рассмотреть эти вопросы для животных, непрерывно растущих в течение всей жизни, и животных, прекращающих рост на определенной стадии развития с сохранением достигнутой массы на протяжении всей оставшейся жизни.

Физическое и биологическое время Физическим временем будем называть время, в котором мы измеряем длительности различных событий, происходящих на Земле. Единицы физического времени определяются скоростью вращения Земли вокруг своей оси и вокруг Солнца. Эти единицы можно считать практически неизменными.

Биологические системы существуют благодаря специфическим процессам, протекающим в них с определенными скоростями. Каждый из этих процессов может служить основанием для определения собственного, внутреннего (биологического) времени этой системы. Величина единицы внутреннего времени зависит от того, какой именно процесс выбран для ее определения. Скорости одних и тех же процессов, происходящих в разных живых системах, могут быть разными и изменяются с возрастом системы. Поэтому единица внутреннего времени, определенная через любой биологический процесс, есть величина переменная и индивидуальная для каждой системы.

Проблема биологического времени разрабатывается в разных аспектах со второй половины XIX века. Рассматриваются различные биологические системы от белковой молекулы до биосферы. В зависимости от уровня рассмотрения даются разные определения биологического времени. Например, существует определение элементарной единицы биологического времени (цитохрона) как длительности одного деления клетки определенного вида. Для растения это может быть верхушечная стеблевая клетка. Число генетически заложенных делений составляет цитохронный потенциал организма и определяет продолжительность его жизни (Балюра, Балюра, 1996). Краткая история вопроса

Нас интересует то «собственное» время, в котором существует организм как целое. Поэтому за основу мы взяли наиболее наглядные и универсальные для любого организма и любого периода его жизни процессы, скорости которых можно оценить. Это 1) процесс изменения массы и 2) процесс использования энергии (метаболизма), о скорости которого для аэробных организмов можно судить по скорости потребления кислорода.

Общепризнано, что морфологические и физиологические свойства животного тесно связаны с массой тела M. Описано множество аллометрических зависимостей вида Y = aMb . В частности, установлено, что для разных организмов в широком диапазоне масс скорость метаболизма Q эквивалентна М3/4, а продолжительность жизни tmax эквивалентна М1/4. Масса

Известна единственная попытка определения внутреннего времени через процесс роста массы организма (Backman G. Wachstum und organische Zeit. Leipzig: J.A. Barth. , 1943). «Органическое» время Бакмана может быть величиной как положительной, так и отрицательной, а в момент наступления половой зрелости оно равно нулю. Определение Бакмана применялось для описания роста деревьев и не получило широкого распространения.

Бакман выделяет три цикла роста многоклеточного организма: овулярный, эмбриональный и период основного роста. «Органическое» время определяется отдельно для каждого цикла. Основное предположение: между относительным временем T = t/tmax и относительной скоростью роста H = h/hmax существует соотношение , причем k2 < 0. В терминах t и h это предположение имеет вид , где ; . Скорость роста h которая является производной функции роста . Определив органическое время х как , Бакман получает функцию роста в органическом времени , где c0, c1 и с2 выражаются через k0, k1 и k2.

Метаболизм Общепризнанным является способ определения внутреннего (физиологического) времени организма через удельную скорость метаболизма. Наиболее строгое определение дал Дж. Райс (Reiss J.O. The meaning of developmental time: A metric for comparative embryology // Amer. Natur. 1989. V. 134. № 2). Он ввел понятие «удельный метаболизм за время жизни» и определил его как Предположив, что скорость течения физиологического времени пропорциональна удельной скорости метаболизма, Райс дал следующее определение: где ta и tb – соответственно, начало и конец рассматриваемого периода. ( q(t) – удельная скорость метаболизма) Physiological time ,

Из этого определения следует: Физиологическим временем названо количество энергии, использованной единицей массы организма за некоторый интервал физического времени. Физиологическому времени придается размерность [энергия/масса]. Единица физиологического времени имеет размерность [энергия/масса/время]. Райс употребляет выражение «единица физио-логического времени» и понимает «физиоло-гическое время» как соответствующее количество единиц физиологического времени.

Высказано и активно обсуждается предположение, что суммарное за время жизни количество энергии, использованное единицей массы, определяет продолжительность жизни, и что это количество примерно одинаково для животных, стоящих на одной ступени эволюционного развития (Rubner, 1908; Бауэр, 1935; Нагорный, 1940; Brody, 1945; Зотин, Зотин, 1999 и др.).

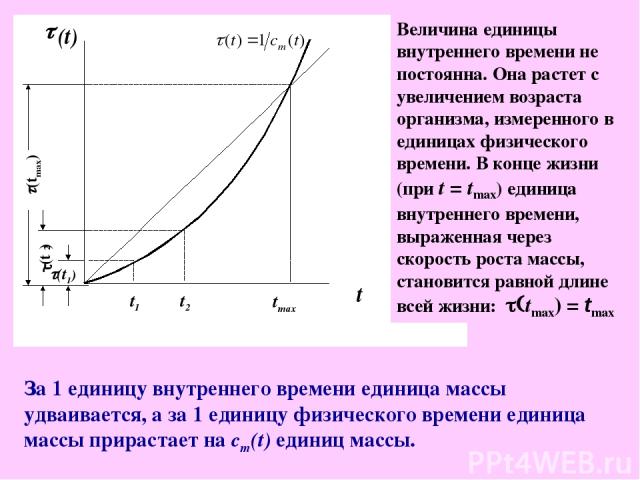
Определение единицы внутреннего времени через скорость роста массы организма Обозначим: – функция изменения массы организма с возрастом t, выраженном в единицах физического времени ([M]); – скорость изменения массы ([MT-1]); – удельная скорость роста (скорость роста единицы массы) ([T-1]). Определим: – единица внутреннего времени ([T]). t(t) – это время, за которое единица массы, растущая со скоростью cm(t), прирастает на единицу массы, т.е. воспроизводит саму себя (время удвоения массы). Определение имеет смысл только для животных, непрерывно растущих в течение всей жизни, или для периода роста массы, когда m’(t) > 0. При снижении массы оказывается t(t) < 0, при неизменной массе t(t) не существует.

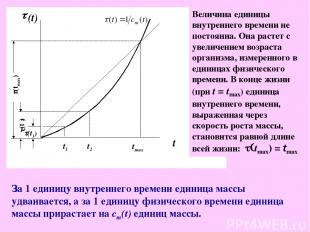
Величина единицы внутреннего времени не постоянна. Она растет с увеличением возраста организма, измеренного в единицах физического времени. В конце жизни (при t = tmax) единица внутреннего времени, выраженная через скорость роста массы, становится равной длине всей жизни: t(tmax) = tmax За 1 единицу внутреннего времени единица массы удваивается, а за 1 единицу физического времени единица массы прирастает на cm(t) единиц массы.

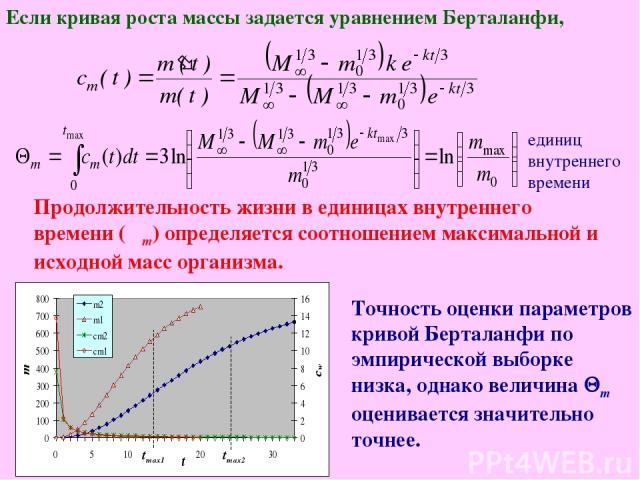
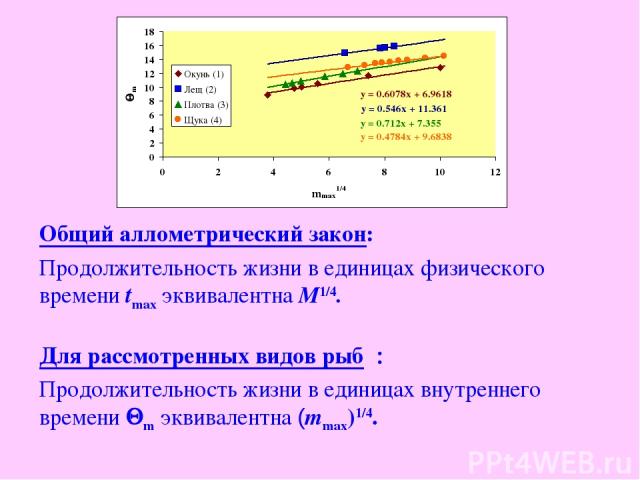
За одну единицу физического времени единица массы прирастает на cm(t) единиц массы. Поэтому одна единица физического времени содержит в себе cm(t) единиц внутреннего времени, причем это количество изменяется с изменением t. Суммарное количество единиц внутреннего времени, содержащееся во всем периоде жизни организма, является продолжительностью жизни, выраженной в единицах внутреннего времени (Qm): , tmax – продолжительность жизни в единицах физического времени. Для расчетов величины Qm необходимо знать функцию роста массы m(t) и продолжительность жизни tmax. Пример непрерывно растущих животных – рыбы.

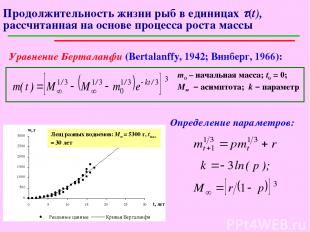
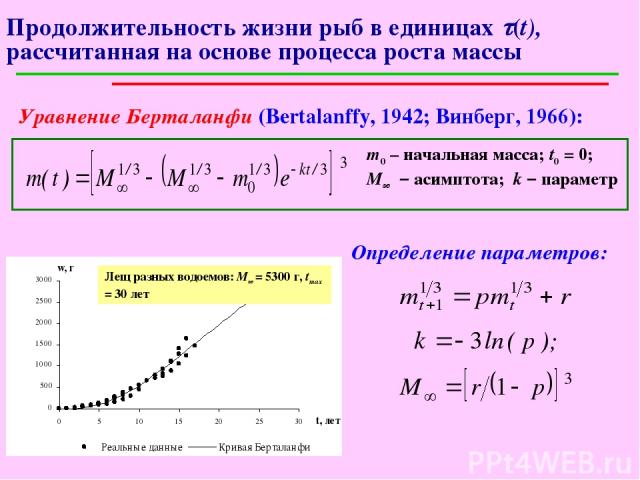
Продолжительность жизни рыб в единицах t(t), рассчитанная на основе процесса роста массы Уравнение Берталанфи (Bertalanffy, 1942; Винберг, 1966): m0 – начальная масса; t0 = 0; М∞ – асимптота; k – параметр Определение параметров: Лещ разных водоемов: M∞ = 5300 г, tmax = 30 лет

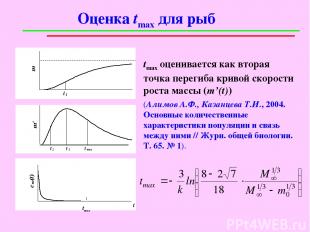
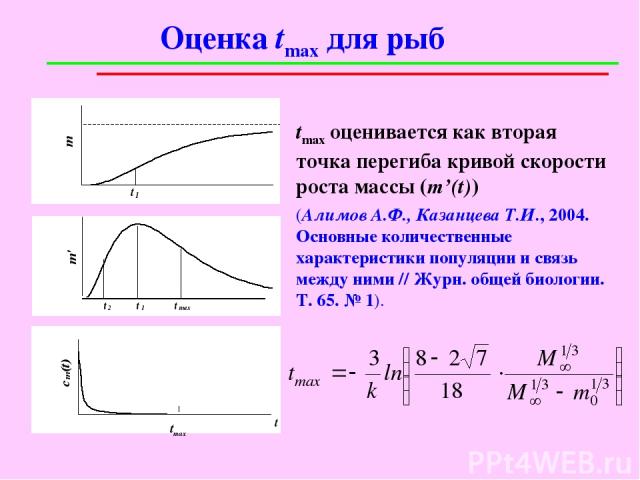
Оценка tmax для рыб tmax оценивается как вторая точка перегиба кривой скорости роста массы (m’(t)) (Алимов А.Ф., Казанцева Т.И., 2004. Основные количественные характеристики популяции и связь между ними // Журн. общей биологии. Т. 65. № 1).

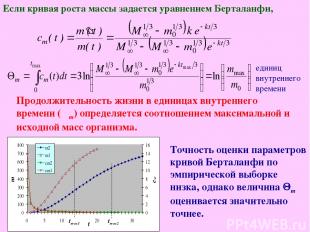
Точность оценки параметров кривой Берталанфи по эмпирической выборке низка, однако величина Qm оценивается значительно точнее. единиц внутреннего времени Продолжительность жизни в единицах внутреннего времени (Θm) определяется соотношением максимальной и исходной масс организма. Если кривая роста массы задается уравнением Берталанфи,

Результаты расчетов величины Qm [ед. внутр. времени] для некоторых популяций рыб из разных водоемов (m0, M∞, mmax [г]; tmax [годы] ) Среднее значение Qm = 12.68 ± 0.39 , n = 25 Вид, водоем m0 p r k M∞ tmax mmax Qm ОКУНЬ (ЖЕМЧУЖНОЕ) 0.026 0.92 ± 0.04 0.78 ± 0.13 0.24 1039 23 629 10.09 ОКУНЬ (РУБАНКОВО) 0.026 0.92 ± 0.07 0.74 ± 0.21 0.25 810 23 507 9.88 ГУСТЕРА (ВОЛГОГР. ВОДОХР.) 0.005 0.91 ± 0.04 1.09 ± 0.15 0.28 1867 20 1131 12.25 ЕРШ (РУБАНКОВО) 0.001 0.67 ± 0.06 1.08 ± 0.16 1.22 34 5 22 10.38 ЛЕЩ (ЖИЖИЦКОЕ) 0.001 0.95 ± 0.03 1.00 ± 0.20 0.17 6111 34 3772 15.65 ЛЕЩ (ЛОКНОВО) 0.001 0.92 ± 0.02 1.23 ± 0.10 0.27 3087 21 1855 14.94 ПЛОТВА (ЖЕМЧУЖНОЕ 1) 0.011 0.95 ± 0.05 0.75 ± 0.18 0.16 2908 35 1788 12.00 ПЛОТВА (ЖЕМЧУЖНОЕ 2) 0.011 0.94 ± 0.08 0.78 ± 0.24 0.20 1876 29 1161 11.57 ПЛОТВА (СОМИНО) 0.011 0.89 ± 0.16 0.96 ± 0.52 0.34 754 17 470 10.66 ПЛОТВА (ЧЕРНЯВСКОЕ) 0.011 0.90 ± 0.07 0.98 ± 0.26 0.31 1013 18 612 10.93 ЩУКА (КРАСНЕНЬКОЕ) 0.005 0.91 ± 0.08 1.66 ± 0.37 0.29 5762 19 3465 13.37 ЩУКА (ЖЕМЧУЖНОЕ) 0.005 0.89 ± 0.13 2.22 ± 0.90 0.37 7525 15 4496 13.63 ЩУКА (ЧЕРНЯВСКОЕ) 0.005 0.88 ± 0.05 2.17 ± 0.38 0.37 6490 15 3912 13.49 ЩУКА (УЖО) 0.005 0.92 ± 0.05 2.01 ± 0.35 0.27 13259 21 8048 14.22 ЩУКА (КУДО) 0.005 0.88 ± 0.03 2.54 ± 0.28 0.39 8801 14 5261 13.79 ЩУКА (КРИВОЕ) 0.005 0.89 ± 0.03 2.43 ± 0.38 0.36 9675 16 6084 13.94 ЩУКА (СОМИНО) 0.005 0.91 ± 0.09 2.44 ± 0.67 0.30 17411 19 10633 14.49

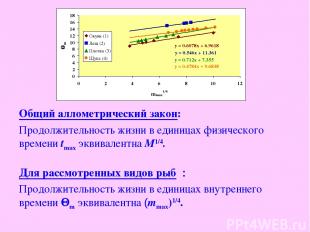
Общий аллометрический закон: Продолжительность жизни в единицах физического времени tmax эквивалентна М1/4. Для рассмотренных видов рыб : Продолжительность жизни в единицах внутреннего времени Qm эквивалентна (mmax)1/4.

Определение единицы внутреннего времени для животных, прекращающих рост, на основе процесса метаболизма Обозначим: M – масса взрослого организма после прекращения роста; Q(t) – количество энергии, потребленной организмом за единицу физического времени (скорость обмена целого организма); – удельная (на единицу массы) скорость обмена. Определим единицу внутреннего времени: – время, за которое единица массы использует одну единицу энергии.

Количество энергии, усвоенной за интервал времени [t1, t2], численно равно длине этого интервала в единицах внутреннего времени. Максимальный возраст (продолжительность жизни) в единицах внутреннего времени равен В течение жизни характер изменения q(t) может неоднократно меняться. Соответственно, время Qq можно разбить на интервалы Проблемы: описать функцию q(t) и оценить tmax.

Определение q(t) и tmax для птиц Основание: R.E. Ricklefs “Intrinsic aging-related mortality in birds” // J. Avian Biol., 31, 2, 2000. Смертность особей возраста х описана функцией Вейбулла: m0 – компонент, не зависящий от возраста и равный смертности молодых особей, достигших массы М; axb – компонент, зависящий от возраста; b – безразмерный коэффициент; a – коэффициент размерности [T –(b+1)]. Введен параметр размерности [T –1], который интерпретируется как «скорость старения» особей популяции. На реальных данных показано, что w не различается значимо для птиц, живущих в природе или в неволе, поэтому можно считать, что возрастная составляющая смертности зависит только от внутренних причин: axb = w b +1xb .

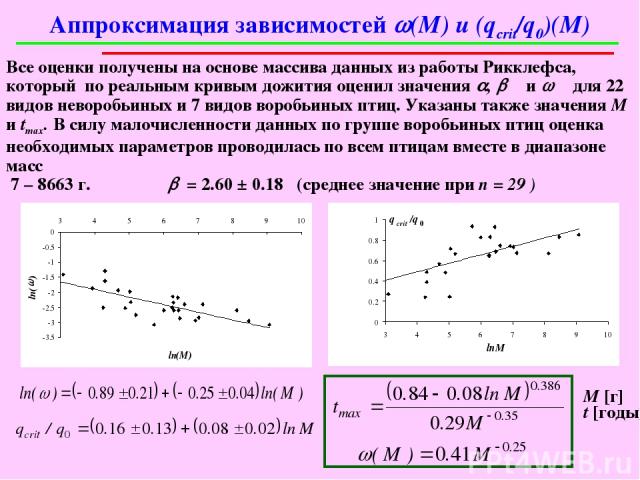
Гипотеза: Внутренней причиной роста смертности с возрастом является уменьшение удельной скорости метаболизма. Нами предложена формула зависимости удельной скорости q(t) метаболизма особи после прекращения роста и достижения массы М от возраста t: – значение q(t) , где в момент прекращения роста, w и b – параметры Риклефса. В конце жизни при t = tmax удельная скорость обмена достигает своего критического значения откуда получаем Таким образом, максимальная (физиологически возможная) продолжительность жизни выражена через величины b = const, w и qcrit /q0 . Если связать w и qcrit/q0 с массой М, получится основанная на процессе метаболизма оценка tmax. ,

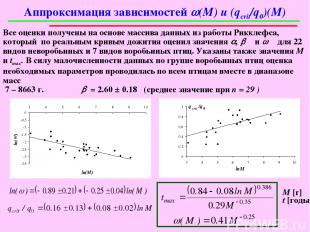
Аппроксимация зависимостей w(M) и (qcrit/q0)(M) Все оценки получены на основе массива данных из работы Рикклефса, который по реальным кривым дожития оценил значения a, b и w для 22 видов неворобьиных и 7 видов воробьиных птиц. Указаны также значения М и tmax. В силу малочисленности данных по группе воробьиных птиц оценка необходимых параметров проводилась по всем птицам вместе в диапазоне масс 7 – 8663 г. b = 2.60 ± 0.18 (среднее значение при n = 29 ) М [г] t [годы]

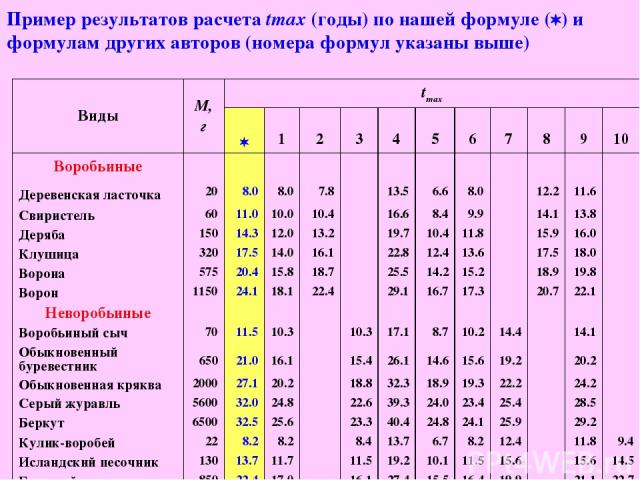
Для оценки качества расчетов tmax по полученной формуле мы применили ее к 33 видам воробьиных и 71 виду неворобьиных, среди которых было 34 вида куликов. Полученные значения сравнили с результатами расчетов по другим известным формулам (Lindstedt,Calder ,1976 [1, 2, 3, 4]; Prinzinger, 1979 [5]; Western, Ssemakula, 1982 [6]; Паевский, 1985 [7, 8]; Гаврилов,1991 [9]; Зотин, Зотин, 1999 [10]) , применив критерий c2 проверки гипотезы об отсутствии значимых различий между двумя случайными выборками. Оказалось, что в половине случаев значимого различия между формулами нет, причем попарное сравнение других формул между собой дает такой же результат. Поэтому наша формула может применяться наравне с другими формулами. Однако она имеет то существенное отличие, что она основана на описании метаболических процессов, происходящих в организме.

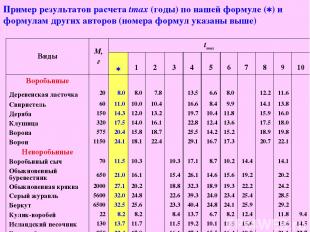
Пример результатов расчета tmax (годы) по нашей формуле ( ) и формулам других авторов (номера формул указаны выше) Виды М, г tmax 1 2 3 4 5 6 7 8 9 10 Воробьиные Деревенская ласточка 20 8.0 8.0 7.8 13.5 6.6 8.0 12.2 11.6 Свиристель 60 11.0 10.0 10.4 16.6 8.4 9.9 14.1 13.8 Деряба 150 14.3 12.0 13.2 19.7 10.4 11.8 15.9 16.0 Клушица 320 17.5 14.0 16.1 22.8 12.4 13.6 17.5 18.0 Ворона 575 20.4 15.8 18.7 25.5 14.2 15.2 18.9 19.8 Ворон 1150 24.1 18.1 22.4 29.1 16.7 17.3 20.7 22.1 Неворобьиные Воробьиный сыч 70 11.5 10.3 10.3 17.1 8.7 10.2 14.4 14.1 Обыкновенный буревестник 650 21.0 16.1 15.4 26.1 14.6 15.6 19.2 20.2 Обыкновенная кряква 2000 27.1 20.2 18.8 32.3 18.9 19.3 22.2 24.2 Серый журавль 5600 32.0 24.8 22.6 39.3 24.0 23.4 25.4 28.5 Беркут 6500 32.5 25.6 23.3 40.4 24.8 24.1 25.9 29.2 Кулик-воробей 22 8.2 8.2 8.4 13.7 6.7 8.2 12.4 11.8 9.4 Исландский песочник 130 13.7 11.7 11.5 19.2 10.1 11.5 15.6 15.6 14.5 Большой кроншнеп 850 22.4 17.0 16.1 27.4 15.5 16.4 19.9 21.1 22.7

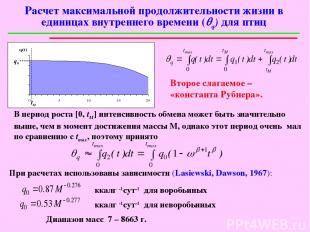
Расчет максимальной продолжительности жизни в единицах внутреннего времени (qq) для птиц q0 tM q0 tM В период роста [0, tM] интенсивность обмена может быть значительно выше, чем в момент достижения массы М, однако этот период очень мал по сравнению с tmax, поэтому принято При расчетах использованы зависимости (Lasiewski, Dawson, 1967): ккал г -1 сут-1 для воробьиных ккал г -1 сут-1 для неворобьиных Диапазон масс 7 – 8663 г. Второе слагаемое – «константа Рубнера».

Удельная скорость обмена выражена в [ккал/г/год]; Результаты расчетов Значения продолжительности жизни в единицах внутреннего времени для групп воробьиных и неворобьиных птиц существенно различаются (в среднем в 1.5 раза), однако внутри групп различия не столь велики. Для неворобьиных птиц эта величина составляет примерно 600 ед., для воробьиных – 950 ед. и определяется она уже не массой птицы, а особенностями метаболических процессов данных групп организмов. Группы n Массы (г) Средние qq Неворобьиные 76 22 - 8660 602 ± 2.5 Воробьиные 41 6 - 1150 963 ± 6.3

Предположения, лежащие в основе всего сказанного выше, имеют общий характер. Поэтому данный подход можно применить к любым животным, прекращающим рост после достижения определенной массы. Проблема заключается в том, чтобы оценить необходимые параметры.

Выводы Предложены способы определения максимальной продолжительности жизни животных ( tmax ), учитывающие особенности их роста и метаболизма. Рассчитаны максимальные продолжительности жизни в единицах внутреннего времени для рыб на основе процесса роста и для птиц на основе процесса метаболизма. В обоих случаях при довольно значительных внутри- и межвидовых различиях в оценках tmax различия в оценках максимальной продолжительности жизни в единицах внутреннего времени не столь велики.

Благодарим за внимание