Презентация на тему: Динамика численности популяций

Интегрированный урок биологии - информатики «Динамика биологических популяций» «Математическое моделирование. Биологические модели развития популяций» Учитель биологии Учитель информатики

Биология и информатика

Тема урока: Динамика популяций План урока 1. Динамика популяций, как биологическое явление. 2. Рост популяции. Типы роста. 3. Колебания численности в популяциях. 4. Способы регуляции численности популяций. 5. Модели развития популяций. 6. Математическое моделирование. 7. Компьютерный эксперимент в электронных таблицах «Excel».

Популяция, её показатели Популяция – это группа одновидовых организмов, занимающих определенный участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций. Условия, влияющие на численность популяции – пищевые ресурсы, ограниченность ареала обитания, эпидемии, болезни, природные катастрофы и т.д. Ёмкость среды – способность территории вмещать определённое количество особей. – биомасса, плотность расселения, общая численность, скорость роста численности, продолжительность жизни, рождаемость, смертность, возрастной состав. Демографические показатели – это единица вида и эволюции. – элементарная эволюционная единица, именно на уровне популяций идет эволюция.

Примеры популяций

Динамика популяций Цель урока 1. Сформировать знания о динамике популяций как о необходимом атрибуте жизни организма, способе их адаптации к постоянно меняющимся условиям существования. 2. Ознакомиться с характерными типами роста популяций как с общими свойствами, передающими их способность к восстановлению численности. 3. Сформировать знания о характере колебаний численности популяций некоторых видов организмов 4. Ознакомиться с явлением регуляции численности и значением этого явления. 5. Закрепить понятия математического моделирования, и навыки работы с программой «Электронная таблица Excel». Научиться прогнозировать развитие биологических популяций, используя компьютерное моделирование в электронных таблицах.

колебания или изменения численности популяций во времени; Динамика популяций, как биологическое явление Вывод: популяция не может сосуществовать без постоянных изменений, так как за счет них она приспосабливается к изменяющимся условиям среды это процессы изменений ее основных демографических показателей во времени – численности, биомассы, популяционной структуры (возрастного состава).

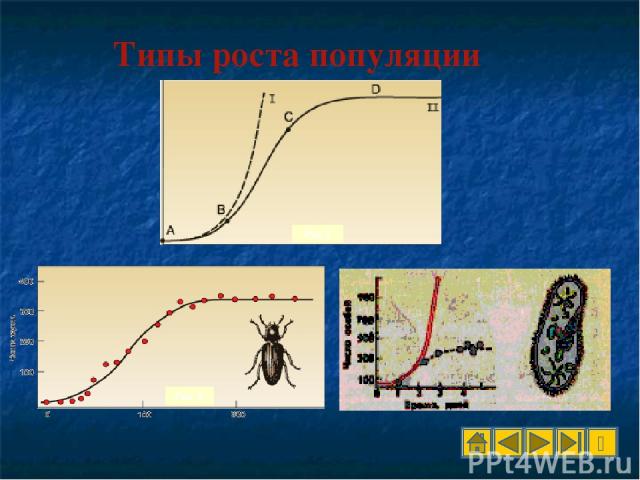
Рост популяции

Рис.1 Рис. 2 Типы роста популяции Рис. 3

Колебания численности особей в популяции Сезонные.

Колебания численности особей в популяции Циклические.

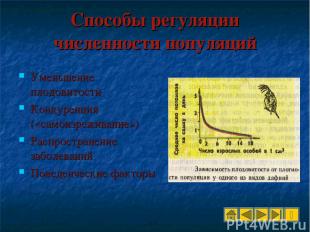
Способы регуляции численности популяций Уменьшение плодовитости Конкуренция («самоизреживание») Распространение заболеваний Поведенческие факторы

модель неограниченного роста (теоретическая); модель ограниченного роста (практическая); модель ограниченного роста с отловом; модель «хищник – жертва» (взаимодействия с другими популяциями). Саранча Сибирский шелкопряд Антилопы Волки загоняют лося Виды моделей развития популяций Корюшка

Основные термины темы «Модели»: Модель - Виды моделей - Способы построения компьютерных моделей - Моделирование - метод познания, состоящий в создании и исследовании моделей. это некий новый упрощенный объект, который отражает существенные особенности реального объекта, процесса или явления. статические, динамические, материальные, информационные. Виды информационных моделей - знаковые, вербальные. на языках объектно-ориентированного программирования и при помощи прикладного программного обеспечения. Виды систем - материальные, нематериальные, смешанные. Формализация - процесс построения информационных моделей с помощью формальных языков.

Основные этапы разработки и исследования моделей на компьютере I. Построение описательной информационной модели. Такая модель выделяет существенные, с точки зрения целей проводимого исследования, свойства (параметры) объекта, а несущественными свойствами пренебрегает; II. Создание формализованной модели. Описательная информационная модель записывается с помощью какого-либо формального языка.; III. Построение компьютерной модели. Формализованная информационная модель преобразуется в компьютерную модель, т.е. записывается на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели: создание проекта на одном из языков объектно-ориентированного программирования (Visual Basic, Delphi) или с помощью прикладного программного обеспечения (MS Excel, MS Word); IV. Компьютерный эксперимент и визуализация формальных моделей. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты. Если компьютерная модель исследуется в приложении, например, в электронных таблицах, можно построить таблицы, диаграммы или графики, провести сортировку или поиск данных и т.д.; V. Анализ полученных результатов и корректировка модели.

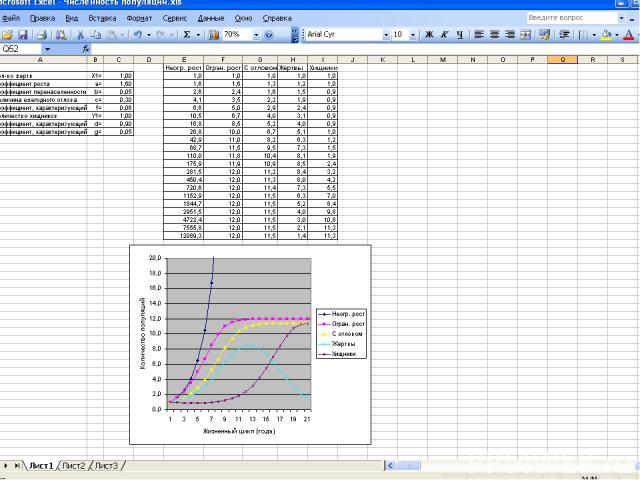
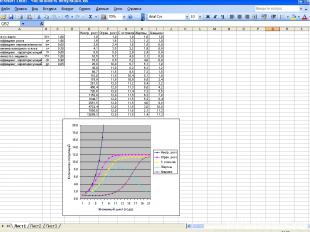
где xn+1 – численность популяции следующего года, xn – численность популяции текущего года, а – коэффициент роста (если рост 5%, то а = 1,05). Информационные модели развития популяций В этой модели численность популяции ежегодно увеличивается на определённый процент. Никакие абиотические (внешние) и биотические (внутренние) факторы влиять на численность популяции в этой модели не будут. Модель теоретическая. Модель неограниченного роста ,

В этой модели учитывается, что на численность популяции оказывает влияние состояние окружающей среды, наличие корма, перенаселённость и другие факторы Модель ограниченного роста , где xn+1 – численность популяции следующего года, xn – численность популяции текущего года, а – коэффициент роста, b – коэффициент перенаселённости.

В этой модели учитывается, что на численность популяций промысловых животных и рыб также оказывает влияние величина ежегодного отлова. Модель ограниченного роста с отловом где x n+1 – численность популяции следующего года, x n – численность популяции текущего года, а – коэффициент роста, b – коэффициент перенаселённости, с – величина ежегодного отлова, ,

Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (караси-щуки, зайцы-волки и т.д.). В этой модели количество жертв и хищников связано между собой. Модель «хищник – жертва» , Количество встреч жертв и хищников прямо пропорционально произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищником, xn – количество жертв, yn – количество хищников.

Типы данных в MS Excel Текст, число, формула Относительная адресация ячеек – (А1, D23, A1 : F5, ...) Адресация, допускающая автоматическую корректировку формулы при её перемещении и копировании. При этом относительные адреса ячеек, входящие в формулу, изменяются в соответствии с её перемещением относительно исходной ячейки. Абсолютная адресация ячеек - ($A$1, $A$1 : $F$5,...) Адресация, запрещающая автоматическую корректировку ячеек с абсолютной адресацией при перемещении и копировании формулы. При этом абсолютные адреса ячеек, входящие в формулу, не изменяются при её перемещении относительно исходной ячейки. Как сменить способ адресации ячеек? Нажать клавишу F4, установив курсор в формуле после адреса нужной ячейки. Что происходит при изменении данных в ячейке, на которую ссылается формула? Автоматический перерасчёт всей таблицы, изменение данных в тех ячейках, которые связаны с данной ячейкой. Повторим ранее изученный материал, который необходим при построении модели

Значение исследований моделей развития популяций Будущее человечества, жизнь наших детей, внуков и более отдалённых потомков целиком зависят от совместных усилий людей, населяющих Землю сегодня. Академик А. Виноградов, геофизик РОССИИ