Презентация на тему: Закони Кеплера

Закони Кеплера

Йога ннес Ке плер німецький філософ, математик, астроном, астролог і  оптик, відомий насамперед відкриттям законів руху планет, названих законами Кеплера на його честь. В обчислювальній математиці на його честь названо метод наближеного обчислення інтегралів. Він поширював логарифмічне числення у Німеччині, заснував оптику як науку, вдосконалив телескоп-рефрактор та допоміг довести відкриття, зроблені з допомогою телескопа його сучасником Ґалілео Ґалілеєм. Йога ннес Ке плер німецький філософ, математик, астроном, астролог і  оптик, відомий насамперед відкриттям законів руху планет, названих законами Кеплера на його честь. В обчислювальній математиці на його честь названо метод наближеного обчислення інтегралів. Він поширював логарифмічне числення у Німеччині, заснував оптику як науку, вдосконалив телескоп-рефрактор та допоміг довести відкриття, зроблені з допомогою телескопа його сучасником Ґалілео Ґалілеєм.

Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. Названо на честь німецького астронома Йоганес Кеплера, який відкрив їх шляхом аналізу спостережень руху Марса навколо Сонця, здійснених данським астрономом Тихо Браге. Закони Кеплера - три емпіричні залежності, що описують рух планет навколо Сонця. Названо на честь німецького астронома Йоганес Кеплера, який відкрив їх шляхом аналізу спостережень руху Марса навколо Сонця, здійснених данським астрономом Тихо Браге.

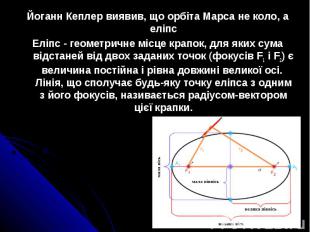
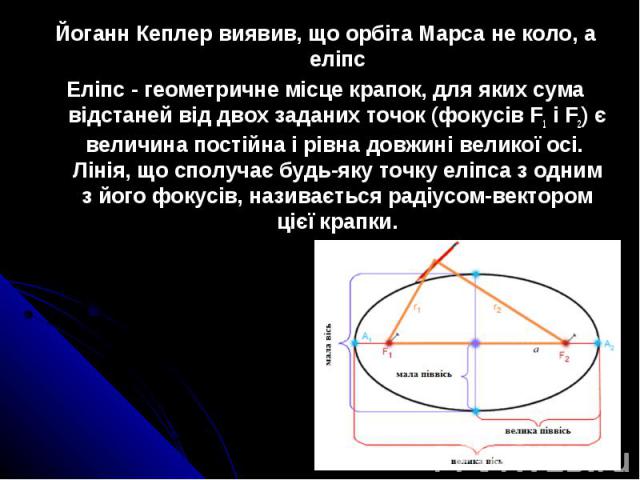
Йоганн Кеплер виявив, що орбіта Марса не коло, а еліпс Йоганн Кеплер виявив, що орбіта Марса не коло, а еліпс Еліпс - геометричне місце крапок, для яких сума відстаней від двох заданих точок (фокусів F1 і F2) є величина постійна і рівна довжині великої осі. Лінія, що сполучає будь-яку точку еліпса з одним з його фокусів, називається радіусом-вектором цієї крапки.

Закони Кеплера застосовні не лише для руху планет, але і для руху їх природніх і штучних супутників. Закони Кеплера застосовні не лише для руху планет, але і для руху їх природніх і штучних супутників.

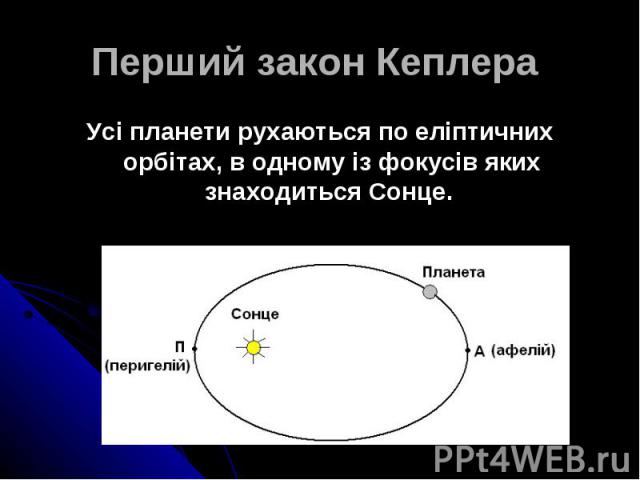
Перший закон Кеплера Усі планети рухаються по еліптичних орбітах, в одному із фокусів яких знаходиться Сонце.

Другий закон Кеплера. За рівні проміжки часу радіус-вектор планети описує рівні площі ∆S = L·∆t/2m

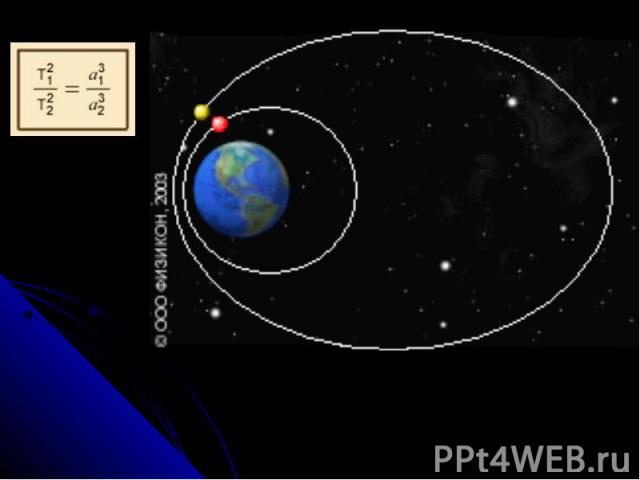
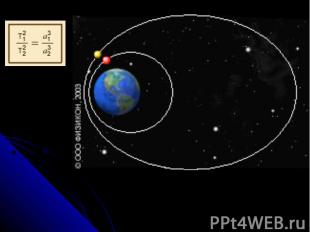
Третій закон Кеплера Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт. Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти. Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті. Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон

Підготували: Побережна Марія Олексюк Аліна Синюшко Дмитро Шаталюк Денис