Презентация на тему: Моделирование многогранников архимедовы тела

Моделирование многогранниковархимедовы телаурок геометрии10 класс Логинова Ирина Викторовна, «Школа развития способностей «Крошка Енот», преподаватель «Логики» и «Наглядной геометрии»Великий Новгород 2010

СОДЕРЖАНИЕТела Архимеда.Развертка многогранника.Усеченный куб. Усеченный тетраэдр. Усеченный октаэдр. Усеченный икосаэдр.Кубооктаэдр.ИкосододекаэдрРомбокубооктаэдр.Ромбоикосододекаэдр.Ромбоусеченный кубооктаэдр.Курносый куб.Курносый додекаэдр.Исследование. Оборудование для моделирования.Таблица№1 «Результаты исследования».Таблица №2 «Результаты исследования» (ответы).Литература.

Кроме правильных, существует тринадцать многогранников, которые впервые открыл и описал Архимед – это тела Архимеда. Все многогранные углы у них равны, а грани – правильные многоугольники разных видов. Причем в каждой вершине сходится одно и тоже количество граней.

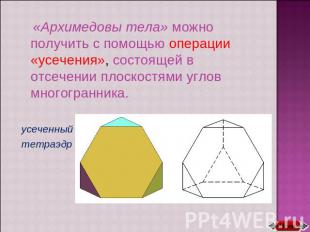
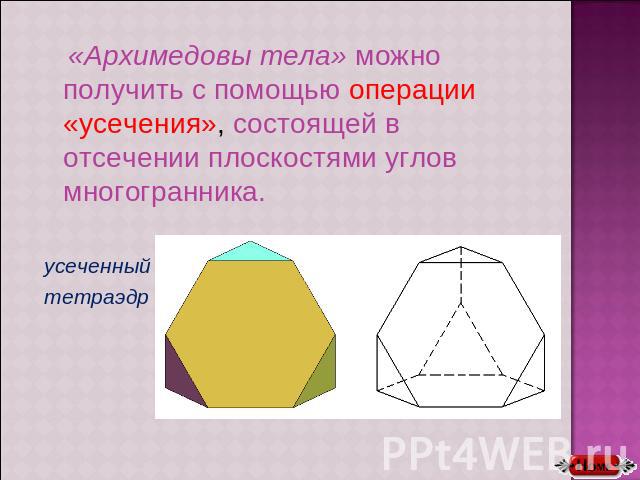
«Архимедовы тела» можно получить с помощью операции «усечения», состоящей в отсечении плоскостями углов многогранника.усеченныйтетраэдр

Если поверхность многогранника разрезать по некоторым ребрам и развернуть ее на плоскость так, чтобы все многоугольники, входящие в эту поверхность, лежали в данной плоскости, то полученная фигура на плоскости называется развертка кубооктаэдра разверткой многогранника.

Развертка усеченного куба

Усеченный тетраэдр

Развертка усеченного тетраэдра

Усеченный октаэдр

Развертка усеченного октаэдра (2 части)

Усеченный икосаэдр

Развертка усеченного икосаэдра

кубооктаэдр

Развертка кубооктаэдра (2 части)

икосододекаэдр

Развертка икосодекаэдра (2 части)

ромбокубооктаэдр

Развертка ромбокубооктаэдра

ромбоикосододекаэдр

Развертка ромбоикосододекаэдра

Ромбоусеченныйкубооктаэдр

Развертка ромбоусеченного кубооктаэдра

Курносый куб

Развертка курносого куба

Курносый додекаэдр

Развертка курносого додекаэдра

Исследование Собери из ТИКО-деталей многогранники и ответь на вопросы:Сколько вершин у многогранника?Сколько ребер у многогранника?Сколько граней у многогранника?Из каких граней составлен многогранник? Сколько их? Заполни таблицу.ОБОРУДОВАНИЕ ДЛЯ МОДЕЛИРОВАНИЯ:геометрический конструкторТИКО.

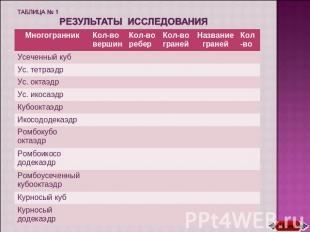
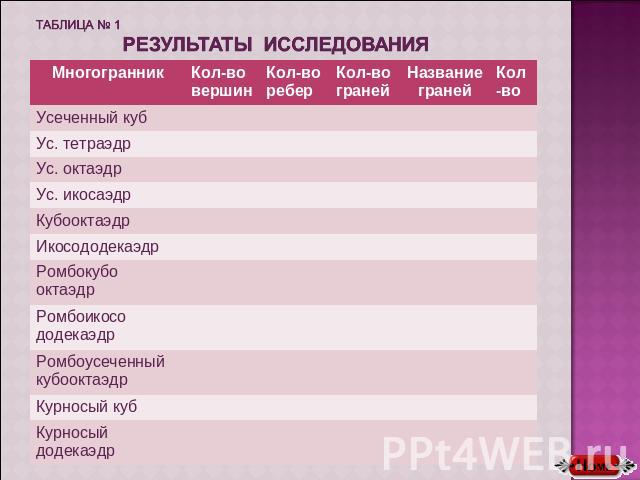
таблица № 1 результаты исследования

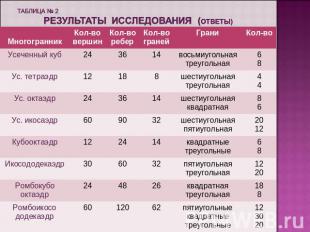
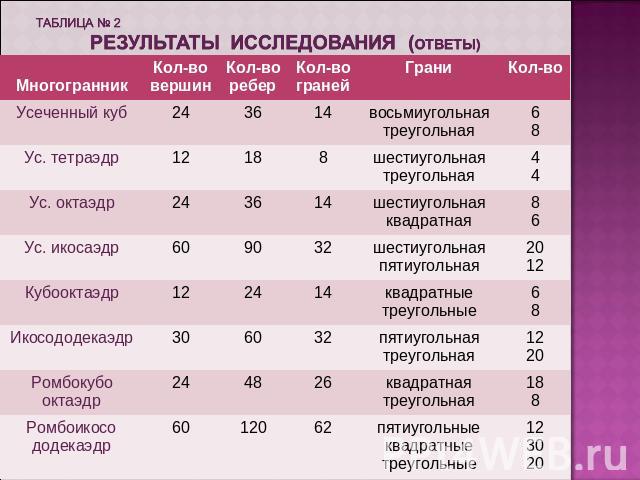
таблица № 2 результаты исследования (ответы)

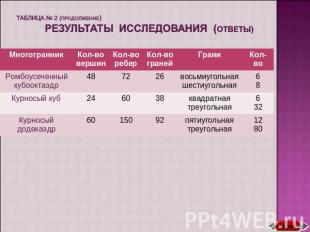
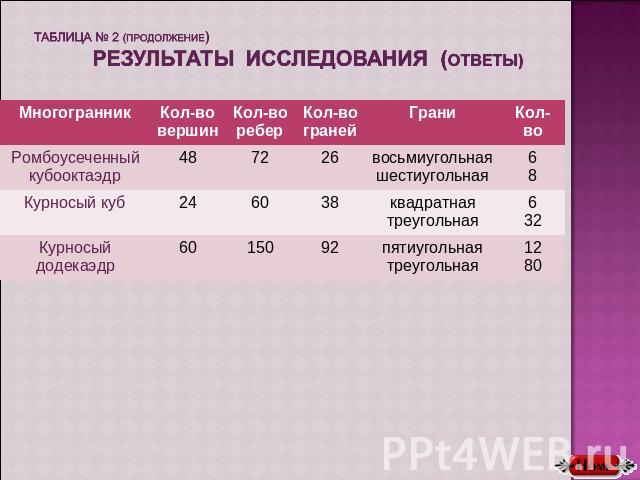
таблица № 2 (продолжение) результаты исследования (ответы)

литература Атанасян Л. С. И др. Учебник по геометрии 10 – 11 класс. – Просвещение, 2002.