Презентация на тему: Цифровые устройства и микропроцессоры

ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ

ТЕМА 1. СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ Цифровые устройства и цифровая информация

Цифровая обработка радиосигналов Все физические процессы, в том числе и радиотехнические сиг­налы, являются непрерывными (аналоговыми). Часто на практике возникает необходимость преобразования таких сигналов к виду, пригодному для обработки цифровыми устройствами. Преимущества цифровых методов обработки радиосигналов очевидны и заключаются в обеспечении высокой точности, стабильности параметров, недостижимых при аналоговой обработке. Цифровые схемы проектируются на основе одного или нескольких типов логических элементов, что существенно повышает технологичность их производства. В то же время аналоговые схемы содержат элементы с разными номиналами и потому требуют настройки. Стабильность цифровых устройств обеспечивается тем, что логические элементы имеют два устойчивых разграниченных состояния, которые сохраняются даже при воздействии внешних дестабилизирующих факторов (например температурных). Обработка сигналов цифровыми методами позволяет достичь прямоугольной формы одного из основных параметров фильтров амплитудно-частотной характеристики.

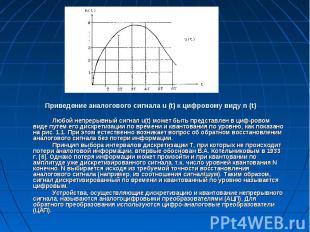
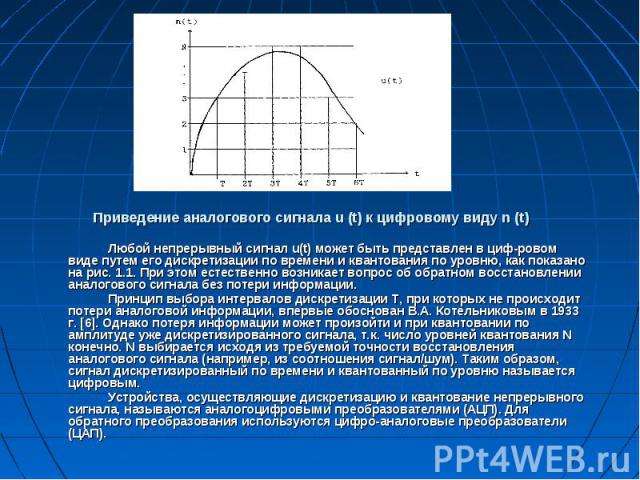
Приведение аналогового сигнала u (t) к цифровому виду n (t) Любой непрерывный сигнал u(t) может быть представлен в циф­ровом виде путем его дискретизации по времени и квантования по уровню, как показано на рис. 1.1. При этом естественно возникает вопрос об обратном восстановлении аналогового сигнала без потери информации. Принцип выбора интервалов дискретизации Т, при которых не происходит потери аналоговой информации, впервые обоснован В.А. Котельниковым в 1933 г. [6]. Однако потеря информации может произойти и при квантовании по амплитуде уже дискретизированного сигнала, т.к. число уровней квантования N конечно. N выбирается исходя из требуемой точности восстановления аналогового сигнала (например, из соотношения сигнал/шум). Таким образом, сигнал дискретизированный по времени и квантованный по уровню называется цифровым. Устройства, осуществляющие дискретизацию и квантование непрерывного сигнала, называются аналогоцифровыми преобразователями (АЦП). Для обратного преобразования используются цифро-аналоговые преобразователи (ЦАП).

Основные логические функции Математический аппарат, используемый при проектировании ЦУ, основан на алгебре-логике (булевой алгебре). Основными функциями булевой алгебры являются дизъюнкция, конъюнкция и инверсия. Дадим их краткие определения. Дизъюнкция – это логическое сложение (обозначается знаком V и читается ИЛИ). Конъюнкция – логическое умножение (обозначается знаком и читается И). Инверсия – отрицание (обозначается чертой над аргументом и читается НЕ). Данные операции выполняются по вполне определенным правилам, а именно:

Логические тождества Логические тождества

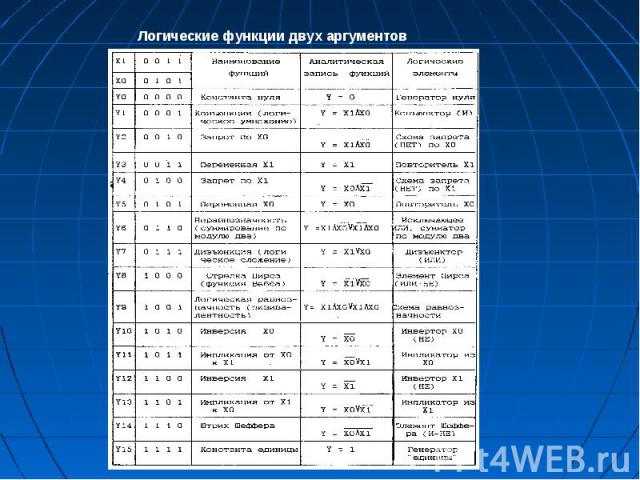
Одна из часто употребляемых логических функций носит название суммирование по модулю 2 и обозначается знаком и выполняется по следующим правилам: 0 0 = 0 0 1 = 1 1 0 = 1 1 1 = 0 Одна из часто употребляемых логических функций носит название суммирование по модулю 2 и обозначается знаком и выполняется по следующим правилам: 0 0 = 0 0 1 = 1 1 0 = 1 1 1 = 0 Замечательной особенностью алгебры-логики является ограниченное число возможных функций. Поскольку каждый аргумент может принимать лишь одно из двух значений (0 или 1), то число возможных комбинаций n аргументов составит: Такому числу комбинаций будет соответствовать следующее число логических функций: Например, когда число аргументов n= 2, получим 16 различных логических функций. В табл. 2.3 приведены все возможные логические функции двух аргументов. С помощью этих функций можно построить сколь угодно сложные функции многих аргументов, а на их основе – цифровые устройства от логических элементов до микропроцессорных систем.

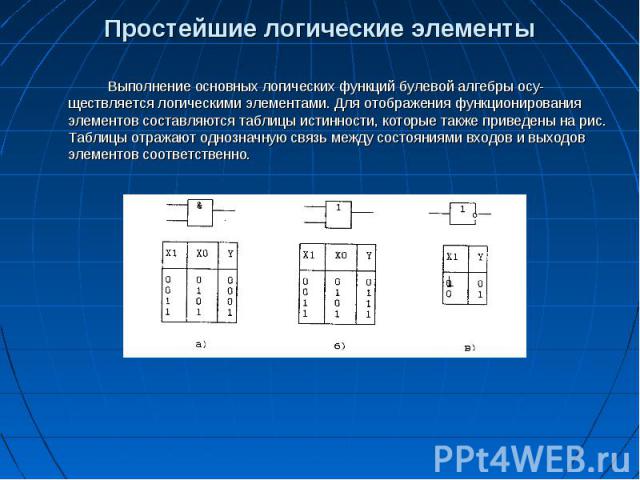
Простейшие логические элементы Выполнение основных логических функций булевой алгебры осу­ществляется логическими элементами. Для отображения функционирования элементов составляются таблицы истинности, которые также приведены на рис. Таблицы отражают однозначную связь между состояниями входов и выходов элементов соответственно.

Функционально полный набор Из таблицы видно, что любую функцию можно выразить через три основные функции булевой алгебры. Это, в свою очередь, позволяет реализовать многовходовые элементы на основе двухвходовых. Набор функций, достаточный для построения любой сколь угодно cложной функции, называется функционально-полной системой логических функций, а соответствующий набор элементов – функционально-полным набором логических элементов (ФПН). ФПН являются наборы, состоящие из конъюнктора, дизъюнктора и инвертора. Такой набор может состоять из двух элементов или даже одного. Примерами могут служить представленные на рис. элементы Пирса и Шеффера, последний из которых является базисным элементом цифровых интегральных микросхем, выполненных на основе транзисторно-транзисторной логики (ТТЛ).

ТЕМА 2. ЦИФРОВЫЕ УСТРОЙСТВА КОМБИНАЦИОННОГО ТИПА Теоретические основы синтеза цифровых устройств. Основы проектирования цифровых устройств. Влияние задержек в логических элементах на функционирование ЦУ. Временные диаграммы. Основы синтеза цифровых устройств без памяти Цифровые устройства, состояние выходов которых зависит только от состояний их входов в данный тактовый момент времени, носят название комбинационных цифровых устройств (КЦУ). Схемотехника КЦУ основана на совокупности логических элементов, составляющих функционально полный набор. Типичными КЦУ являются: кодопреобразователи (шифраторы и дешифраторы), цифровые компараторы, мультиплексоры.

Состязания сигналов Состязания сигналов Проектирование КЦУ проводится на основе математического аппарата булевой алгебры, а это означает, что такой важный параметр, как время (t) не учитывается. Таким образом, не учитываются физические процессы, происходящие в реальных схемах. В логических элементах имеются задержки распространения сигналов, что приводит к нарушению функциональной надежности устройств во время переходных процессов. Задержками обусловлены «состязания» сигналов, которые вызывают неустойчивую работу цифровых устройств. Таким образом, возникает техническое противоречие между математическим моделированием устройств и их реальным функционированием. Состязания сигналов подразделяются на статические и динамические. Состязания называются статическими, если для двух последовательных состояний входов состояние выхода должно остаться неизменным.

Способы борьбы с состязаниями сигналов Для разрешения этого противоречия применяются следующие способы: 1. Подбор задержек элементов таким образом, чтобы задержки в различных ветвях распространения сигнала стали бы равными Для устранения эффекта состязаний в схеме по данному методу необходимо уравнять задержки в ветвях распространения сигнала. Для этого в одну ветвь вводим повторитель, имеющий такую же задержку, как и остальные элементы.

2. Введение дополнительной синхронизации 2. Введение дополнительной синхронизации Этот метод базируется на том, что сигнал на выходе устройства, в котором возникает эффект состязаний, через определенное время принимает правильное значение. Следовательно, если передавать информацию потребителю после завершения переходных процессов, то можно избежать неприятных последствий эффекта состязаний. Для этого в устройство вводят дополнительный логический элемент, который передает сигнал с выхода устройства, если сигнал синхронизации С= =1 равен единице, и имеет состояние «нуль», если С=0. Из приведенного анализа схемы следует, что через ЗТз.ср на ее выходе сигнал принимает правильное значение (переходные процессы завершились). Таким образом, необходимо, чтобы сигнал синхронизации (С=1) появлялся не ранее, чем через 3Tср после изменения значений сигналов на входах.

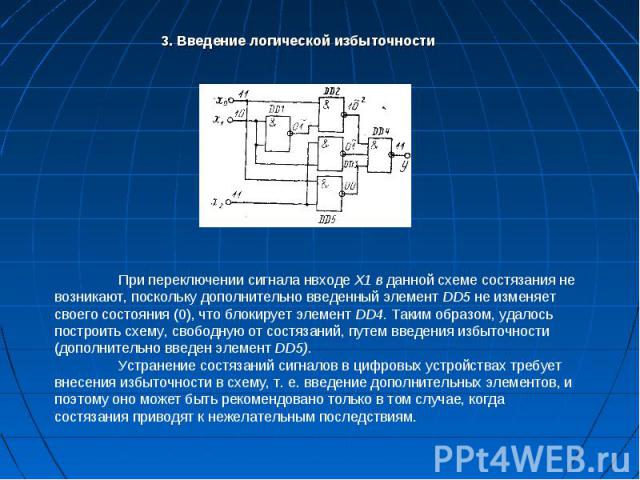
3. Введение логической избыточности 3. Введение логической избыточности

Кодопреобразователи и компараторы Цифровые кодопреобразователи. Применение. Условное графическое обозначение устройств. Схемы. Таблицы истинности

Шифраторы (CD – coder) Шифраторы – это кодопреобразователи, осуществляющие преобра­зование входного кода «1 из m» в двоичный или двоично-десятичный код. Наиболее часто шифраторы применяются для кодирования сигналов от клавиатуры в устройствах с небольшим числом кнопок. Например, с помощью шифратора К155ИВ1 можно передать сигналы от восьми кнопок по трем линиям. ИС К155ИВ1 является не просто кодопреобразователем сигнала «1 из 8» в двоичный код, а приоритетным шифратором: при несоот­ветствии входных сигналов указанному коду код на выходе соответствует нажатой кнопке с максимальным номером.

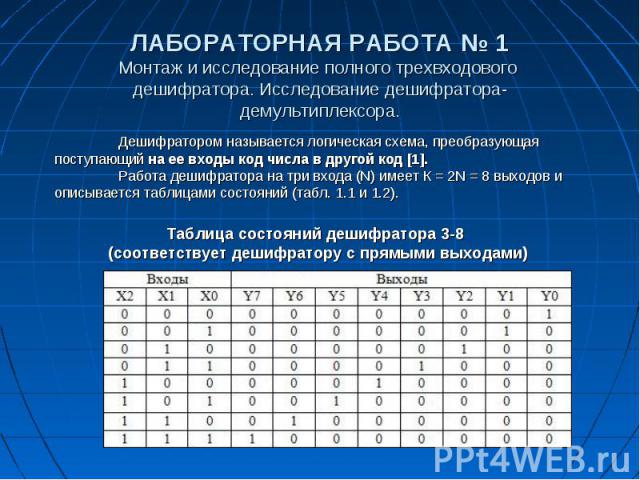
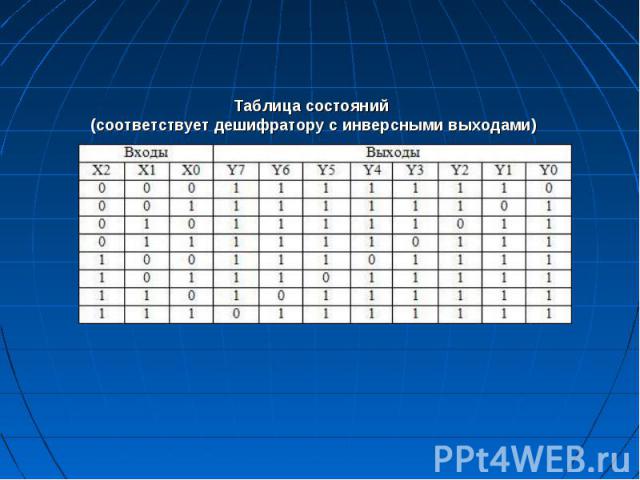
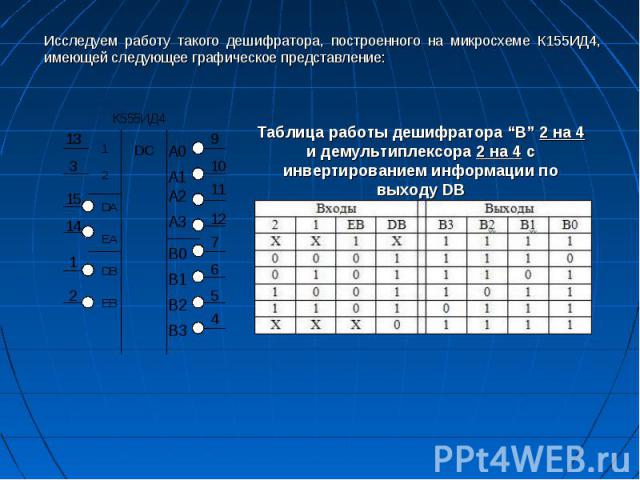
Дешифраторы (DC от слова decoder) Можно сказать (и это было действительно так в первые годы развития цифровой микросхемотехники), что дешифраторы выполняют функцию, обратную шифраторам: преобразуют входной двоичный код в код «1 из m». Дешифраторы выполняют функции, обратные функциям шифраторов, т. е. осуществляют преобразование входного числа, представленного в натуральном двоичном коде, в код «I из т». Иными словами, дешифратор при наличии определенной комбинации на входах обеспечивает появление логической единицы на одном из его выходов. В дешифраторах часто используется синхронизация, разрешающая выработку выходных сигналов только в присутствии разрешающего сигнала С=1.

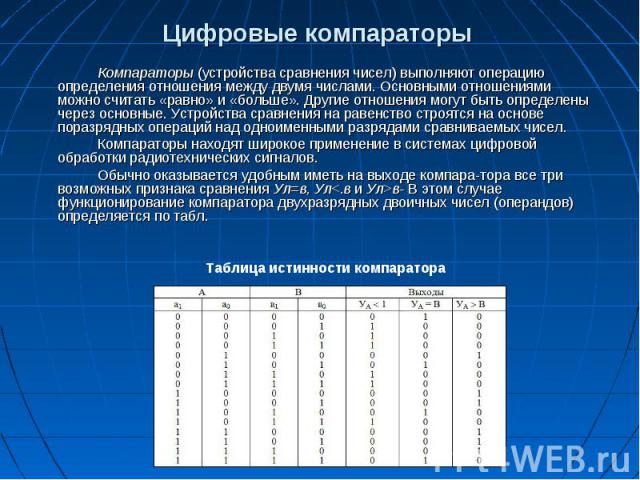
Цифровые компараторы Компараторы (устройства сравнения чисел) выполняют операцию определения отношения между двумя числами. Основными отношениями можно считать «равно» и «больше». Другие отношения могут быть определены через основные. Устройства сравнения на равенство строятся на основе поразрядных операций над одноименными разрядами сравниваемых чисел. Компараторы находят широкое применение в системах цифровой обработки радиотехнических сигналов. Обычно оказывается удобным иметь на выходе компара­тора все три возможных признака сравнения Ул=в, Ул<.в и Ул>в- В этом случае функционирование компаратора двухразрядных двоичных чисел (операндов) определяется по табл.

На рис. приведена схема компаратора СП1, имеющего 11 входов. Четыре пары входов принимают для анализа два четырехразрядных числа А и В. Три входа xA>B, хA<B, xA=B необходимы для наращивания разряд­ности компаратора. Компаратор имеет три выхода результатов сравнения yA<B, yA>B, yA=B. Пять последних строк отображают режим наращивания разрядности, которое может быть последовательным или параллельным. Так, с помощью двух компараторов СП1 можно сравнивать два восьмиразрядных числа. На рис. приведена схема компаратора СП1, имеющего 11 входов. Четыре пары входов принимают для анализа два четырехразрядных числа А и В. Три входа xA>B, хA<B, xA=B необходимы для наращивания разряд­ности компаратора. Компаратор имеет три выхода результатов сравнения yA<B, yA>B, yA=B. Пять последних строк отображают режим наращивания разрядности, которое может быть последовательным или параллельным. Так, с помощью двух компараторов СП1 можно сравнивать два восьмиразрядных числа.

Мультиплексоры (MUX от слова multiplexor) Мультиплексором называется КЦА, осуществляющий передачу логического сигнала с одного из информационных входов на выход в зависимости от комбинации сигналов на управляющих входах. Мультиплексоры используются как многопозиционные переключатели для выборки цифровых каналов или как логические схемы, реализующие любые функции трех (четырехвходовой мультиплексор), четырех (восьмивходовой мультиплексор) и более переменных.

ТЕМА 3. ЦИФРОВЫЕ УСТРОЙСТВА ПОСЛЕДОВАТЕЛЬНОСТНОГО ТИПА Триггеры .Классификация В ЦУ последовательностного типа значения выходных сигналов в данный момент времени определяются значениями входных сигналов в этот же и в предшествующие моменты времени. Предыстория значений входных сигналов фиксируется во внутренних элементах памяти ЦУ.

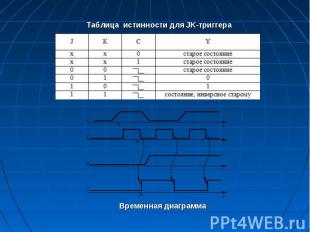
Триггерами принято называть цифровые последовательностные устройства, которые могут находиться в одном из двух устойчивых состояний и переходить из одного состояния в другое под воздействием входных сигналов. Состояние триггера определяется сигналом на выходе Q. Часто триггеры имеют дополнительный инверсный выход Q. Входы триггеров подразделяются на информационные и управляющие. Триггерами принято называть цифровые последовательностные устройства, которые могут находиться в одном из двух устойчивых состояний и переходить из одного состояния в другое под воздействием входных сигналов. Состояние триггера определяется сигналом на выходе Q. Часто триггеры имеют дополнительный инверсный выход Q. Входы триггеров подразделяются на информационные и управляющие. Триггеры отличаются друг от друга выполняемыми функциями, схемой построения, способом управления и т.д. Эти признаки явля­ются основой для их классификации. Классификация триггеров по виду выполняемой логической функции является наиболее важной, поскольку она позволяет определить пригодность данного триггера для выполнения тех или иных операций. Несмотря на потенциальное многообразие видов триггеров, на практике применяются четыре основных типа: – RS-триггер – триггер с раздельной установкой состояний; – информационный D-триггер; – счетный Т-триггер; – универсальный JK-триггер. По способу записи информации триггеры можно разделить на синхронные, асинхронные и универсальные. Состояние выходов синхронных триггеров изменяется лишь в момент прихода разрешающего сигнала на вспомогательный вход синхронизации (или тактирующий вход), при необходимом сочетании сигналов на информационных входах. Асинхронные триггеры не имеют тактирующего входа, и их состояние меняется в момент изменения информационных входных сигналов. В универсальных триггерах имеются как асинхронные, так и тактирующие входы.

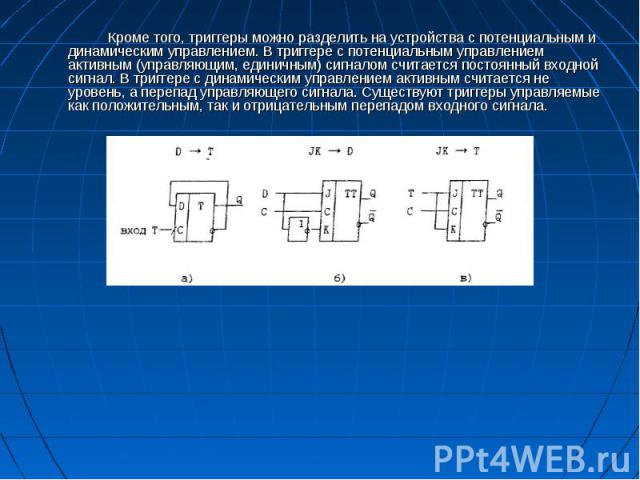
Кроме того, триггеры можно разделить на устройства с потенциальным и динамическим управлением. В триггере с потенциальным управлением активным (управляющим, единичным) сигналом считается постоянный входной сигнал. В триггере с динамическим управлением активным считается не уровень, а перепад управляющего сигнала. Существуют триггеры управляемые как положительным, так и отрицательным перепадом входного сигнала. Кроме того, триггеры можно разделить на устройства с потенциальным и динамическим управлением. В триггере с потенциальным управлением активным (управляющим, единичным) сигналом считается постоянный входной сигнал. В триггере с динамическим управлением активным считается не уровень, а перепад управляющего сигнала. Существуют триггеры управляемые как положительным, так и отрицательным перепадом входного сигнала.

Основные параметры триггеров Подбор типа триггера для использования в качестве функцио­нального элемента схемы не обходится без определения его парамет­ров. Основные параметры триггеров в интегральном исполнении приводятся в справочниках и как паспортные данные. К ним относятся: – нагрузочная способность (N) определяется числом элементов, которые можно подключить к выходу триггера без ущерба функционированию; – задержка переключения триггера Тз.тр (временной интервал между моментами поступления сигнала на вход и реакцией на выходе на этот сигнал); – разрешающее время триггера Т тр (минимальный интервал вре­мени между входными сигналами, при котором не нарушается нормальное функционирование триггера); – максимальная частота переключения триггера Fmax = 1/Tmax

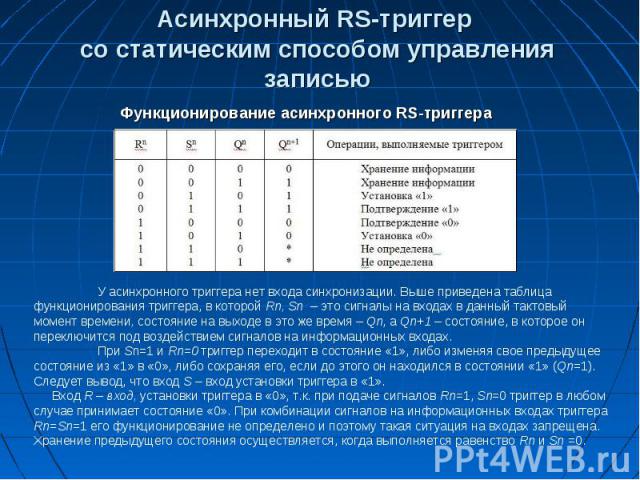
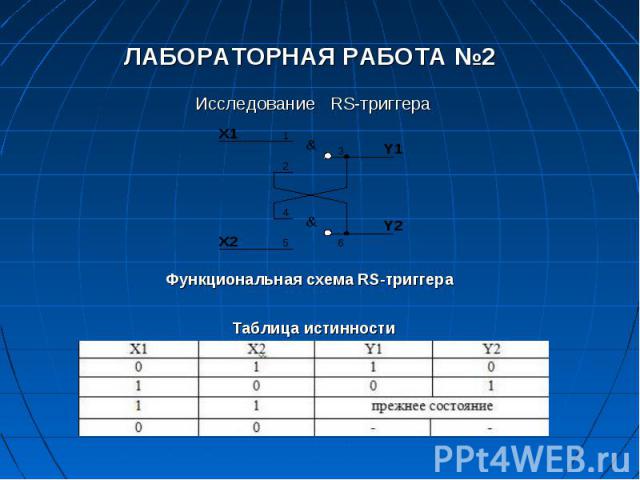
Схемы триггеров. Триггер с установочными входами – RS-триггер (SET – устанавливать, RESET – восстанавливать) Триггером RS типа называют триггер, имеющий два информационных входа R и S. При S=1, R=0 на выходе триггера появляется «1» (Q=1), при S=0, R=1 состояние «0» (Q=0), а при S=0, R=0 сохраняется предыдущее состояние. Данный тип триггеров может быть как синхронным, так и асинхронным. Управление записью информации осуществляется как статическим способом, так и динамическим. Самым простым является асинхронный RS-триггер, который является элементарной ячейкой для построения других типов триггеров и называется конъюнктивной бистабильной ячейкой (КБЯ).

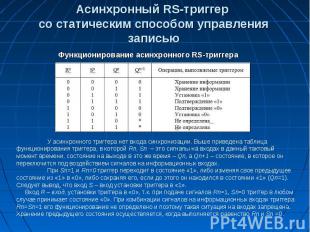
Асинхронный RS-триггер со статическим способом управления записью Функционирование асинхронного RS-триггера

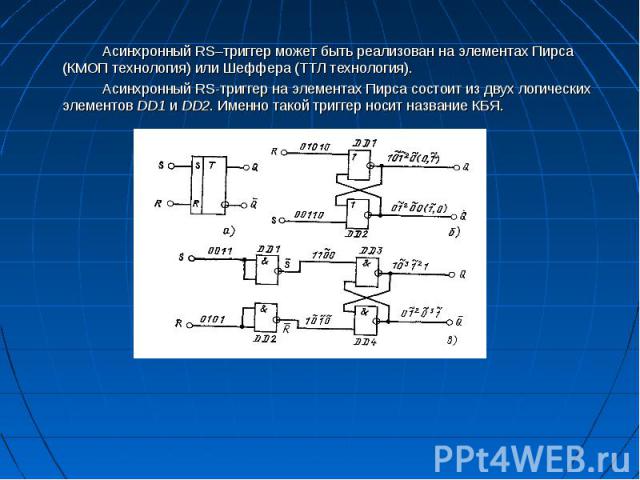
Асинхронный RS–триггер может быть реализован на элементах Пирса (КМОП технология) или Шеффера (ТТЛ технология). Асинхронный RS–триггер может быть реализован на элементах Пирса (КМОП технология) или Шеффера (ТТЛ технология). Асинхронный RS-триггер на элементах Пирса состоит из двух логических элементов DD1 и DD2. Именно такой триггер носит название КБЯ.

Проведенный анализ позволяет установить параметры быстродействия асинхронного RS-триггера на элементах Пирса Проведенный анализ позволяет установить параметры быстродействия асинхронного RS-триггера на элементах Пирса Анализ схемы RS-триггера на двух элементах Шеффера студенты проводят самостоятельно. Следует обратить внимание на то, что входы такого триггера являются инвертированными. Здесь лишь приведем его схему, таблицу функционирования и параметры быстродействия.

Синхронный RS-триггер Синхронный RS-триггер отличается от асинхронного тем, что информация в него записываются только тогда, когда есть разрешающий сигнал на тактовом входе С. На практике в качестве разрешающего может быть сигнал «0», «1» или перепады (положительный 0 1 или отрицательный 1 0). При запрещающем сигнале на информационном входе триггер осуществляет хранение информации.

Анализ работы синхронного RS-триггера на элементах Шеффера, для чего поочередно подадим на входы сигналы в такой последовательности как указано на рис. При С=0 никакие сигналы на информационных входах не изменяют состояние триггера. Анализ работы синхронного RS-триггера на элементах Шеффера, для чего поочередно подадим на входы сигналы в такой последовательности как указано на рис. При С=0 никакие сигналы на информационных входах не изменяют состояние триггера.

Триггер задержки – D (от английского слова delay)

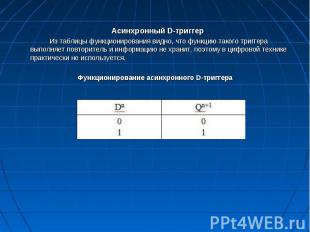
Асинхронный D-триггер Из таблицы функционирования видно, что функцию такого триггера выполняет повторитель и информацию не хранит, поэтому в цифровой технике практически не используется. Функционирование асинхронного D-триггера

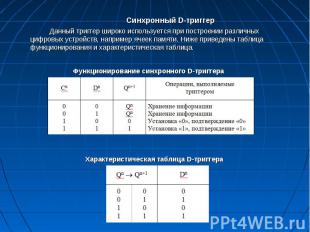
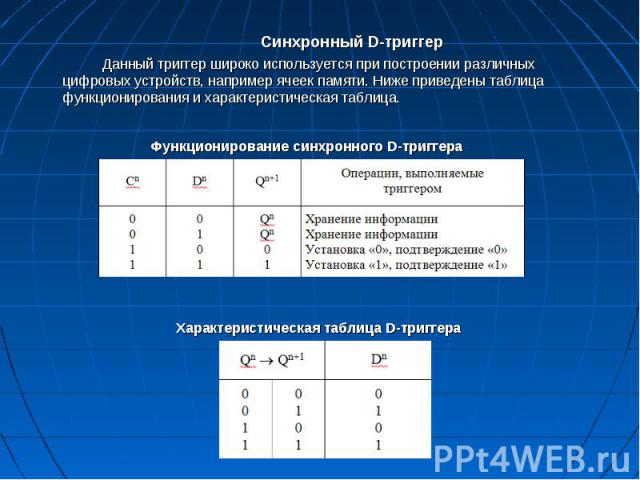
Синхронный D-триггер Синхронный D-триггер Данный триггер широко используется при построении различных цифровых устройств, например ячеек памяти. Ниже приведены таблица функционирования и характеристическая таблица.

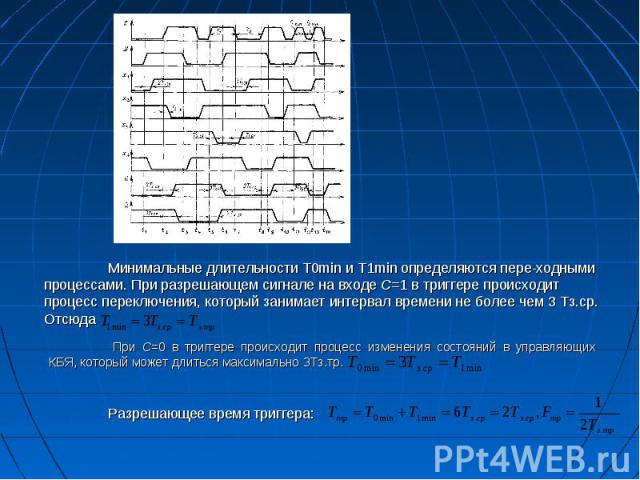
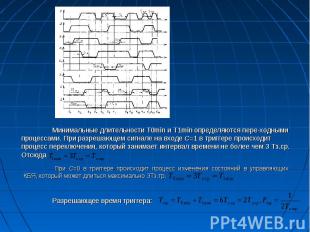
Характеристическое уравнение синхронного D-триггера. D-триггер с динамическим способом управления Характеристическое уравнение синхронного D-триггера. D-триггер с динамическим способом управления Пусть разрешающим сигналом по тактовому входу будет «1». При С = 1 D-триггер со статическим способом управления переходит в режим асинхронной работы, поэтому чаще используют D-триггеры с динамическим способом управления. Рассмотрим работу триггера с использованием временных диаграмм. Пусть на входах присутствуют сигналы «1» (R=S=1). До момента t2 С=0 и триггер находится в режиме хранения информации. Сигналы х2 и х3, влияющие на работу выходной КБЯ, при изменении сигнала на информационном входе D в момент времени t=t1 не изменяют своего значения и остаются равными «1». По диаграммам определяем параметры D-триггера. Задержка переключения триггера равна: Тз.тр=ЗТз.ср. Для на­хождения разрешающего времени триггера (Ттр) необходимо организовать режим повторяющегося переключения триггера. Видно, что период поступления сигналов на вход синхронизации складывается из двух частей: То (когда на тактовом входе низкий потенциал) и T1 (когда – высокий). Для нахождения Ттр необходимо найти минимально возможные длительности Т0 и T1 и тогда

Счетный триггер и JK-триггер. Счетный триггер (от английского слова topple – кувыркаться) Счетным триггером называется триггер, имеющий один информационный вход Т, при подаче сигнала на который триггер меняет свое состояние на противоположное. Счетный триггер находит широкое применение в микропроцессорной технике (например счетчик команд в микропроцессоре).

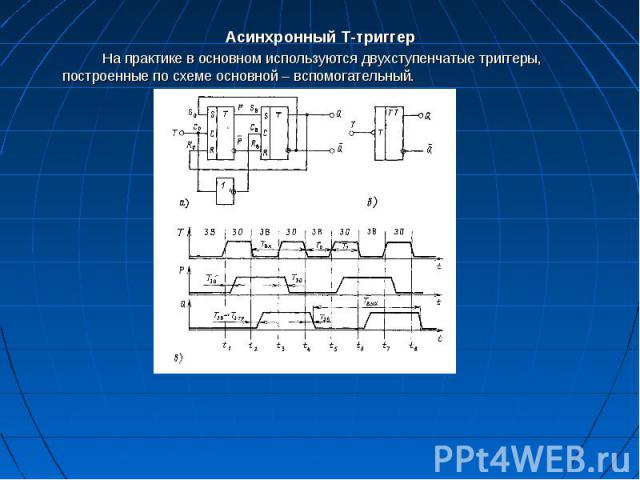
Асинхронный Т-триггер Асинхронный Т-триггер На практике в основном используются двухступенчатые триггеры, построенные по схеме основной – вспомогательный.

Первый триггер называется основным, второй – вспомогательным. Выходы вспомогательного триггера являются выходами всего Т-триггера. Проанализируем работу триггера по временной диаграмме. При t<.t1 (Т = 0) в триггере выполняются два условия: Первый триггер называется основным, второй – вспомогательным. Выходы вспомогательного триггера являются выходами всего Т-триггера. Проанализируем работу триггера по временной диаграмме. При t<.t1 (Т = 0) в триггере выполняются два условия: 1) разрешена перезапись информации из основного триггерa вo вспомогательный, так как сигнал на тактовом входе вспомогательного триггера (Св) равен единице: Св=Т=l, при этом на входах Rв и Sв действуют сигналы с выходов основного триггера Р и Р; 2) запрещена запись информации в основной триггер, т.к. T = Со = 0. В следующий момент времени (t>t1) на входе Т действует сигнал «1», и выполняются два других условия: 1) осуществляется запись новой информации в основной триггер, поскольку Со=Т=1. В основной триггер при Т=1 запишется информация, инверсная по отношению к выходному сигналу. Через время, равное времени задержки переключения основного триггера, новый сигнал появится на его выходах; 2) перезапись информации из основного триггера во вспомогательный запрещена, так как Св=Т=0. Таким образом, переключение триггера происходит в два этапа – сначала (при Т = 1) происходит запись в основной триггер, а затем (при Т = 0) новая информация переписывается во вспомогательный триггер и появляется на выходе устройства. Сигналом, вызывающим переключение триггера, является составной сигнал (высокое напряжение на первом этапе и низкое на втором), т.е. это триггер с динамическим способом управления по отрица­тельному перепаду.

Определим параметры быстродействия триггера. Под задержкой переключения данного двухступенчатого триггера понимается интервал времени между моментом подачи отрицательного перепада на вход и моментом появления сигнала на выходе. Для двухступенчатого триггера задержка переключения вызвана длительностью перезаписи информации из основного триггера во вспомогательный: Определим параметры быстродействия триггера. Под задержкой переключения данного двухступенчатого триггера понимается интервал времени между моментом подачи отрицательного перепада на вход и моментом появления сигнала на выходе. Для двухступенчатого триггера задержка переключения вызвана длительностью перезаписи информации из основного триггера во вспомогательный:

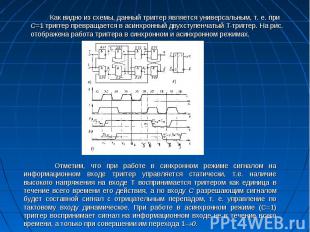
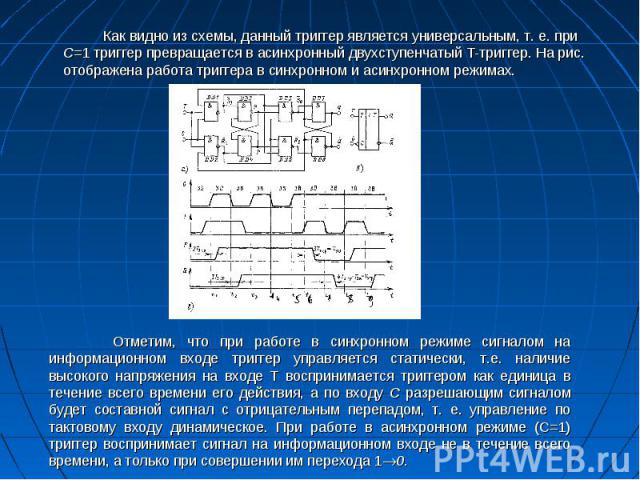
Как видно из схемы, данный триггер является универсальным, т. е. при С=1 триггер превращается в асинхронный двухступенчатый Т-триггер. На рис. отображена работа триггера в синхронном и асинхронном режимах. Как видно из схемы, данный триггер является универсальным, т. е. при С=1 триггер превращается в асинхронный двухступенчатый Т-триггер. На рис. отображена работа триггера в синхронном и асинхронном режимах.

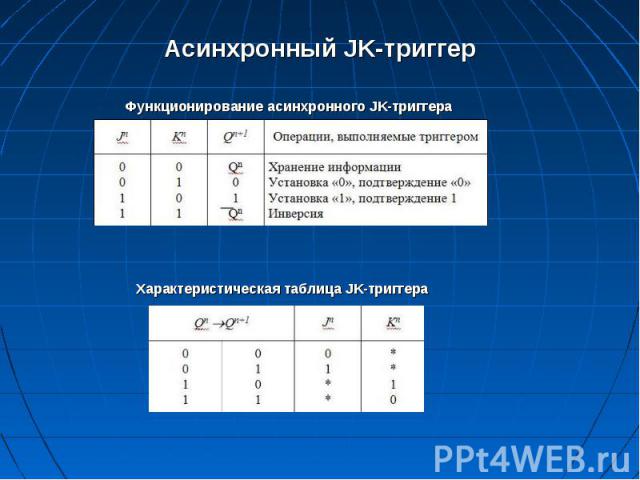
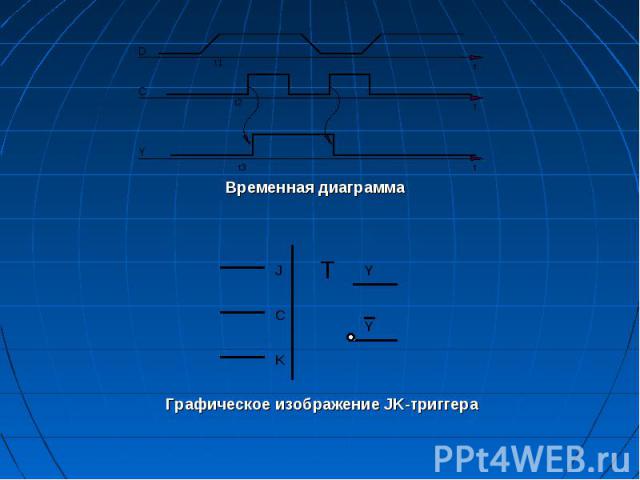
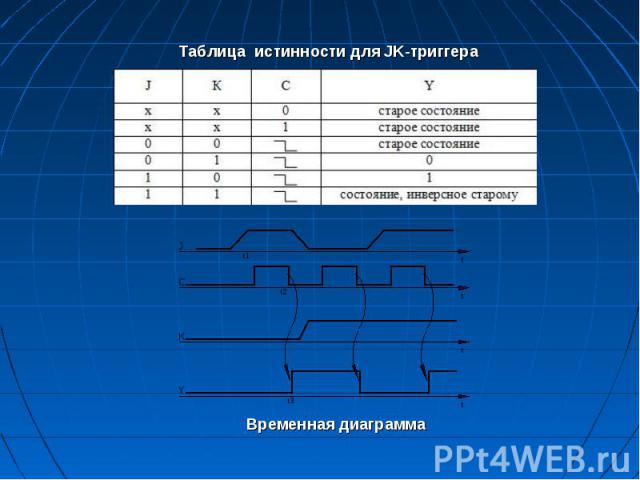
JK-триггер (jark – внезапное включение и kill – внезапное отключение) Триггером JK типа называется триггер с двумя информа­ционными входами J и К., который при J = K =1 осуществляет инверсию предыдущего состояния, а в остальных вариантах функционирует как RS-триггер, причем входу J соответствует вход S, входу К – вход R.

Асинхронный JK-триггер Асинхронный JK-триггер

JK-триггер осуществляет при одной из комбинаций входных аргументов инверсию своего предыдущего состояния и поэтому его реализация со статическим способом управления практически не используется. JK-триггер осуществляет при одной из комбинаций входных аргументов инверсию своего предыдущего состояния и поэтому его реализация со статическим способом управления практически не используется. Данный триггер управляется отрицательным перепадом (1 0). Так, например, чтобы установить триггер в состояние «1», необходимо на вход J подать единицу (K=0) (при этом происходит запись в основной триггер) и затем – сигнал «0» (сигнал «1» переписывается из основного триггера во вспо­могательный). Таким образом, под сигналом «1» на входах J и K двухступенчатого триггера необходимо понимать сигнал вида 1 0, что означает отрицательный перепад напряжения. Параметры быстродействия асинхронного двухступенчато­го триггера совпадают с соответствующими параметрами Т-триггера.

Счетчики. Определение, основные характеристики и классификация счетчиков Счетчиком называется цифровой автомат последовательностного типа, осуществляющий счет и хранение числа подсчитанных сигналов. Счетчики находят весьма широкое применение в радиотехнических системах и микропроцессорной технике для построения устройств синхронизации, осреднения, накопления и т. д. Кроме этого, счетчики используются в качестве делителей частоты следования импульсных последовательностей.

Параметры счетчиков Одним из основных параметров счетчика является модуль счета (Mсч). Модуль счета Мсч – это число, характеризующее количество различных состояний счетчика. После поступления Мсч счетных сигналов счетчик возвращается в исходное состояние.

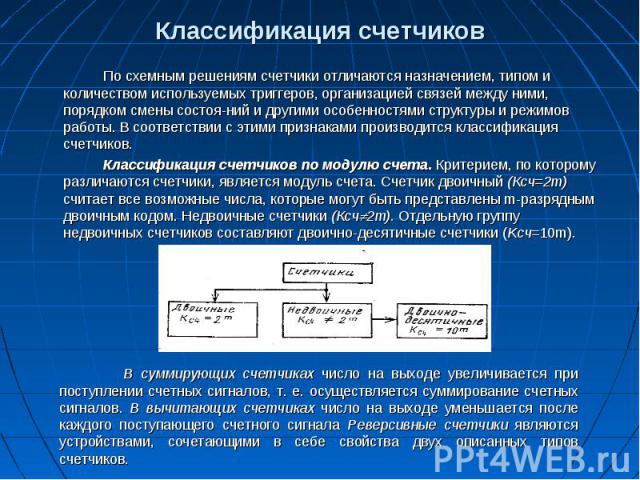
Классификация счетчиков По схемным решениям счетчики отличаются назначением, типом и количеством используемых триггеров, организацией связей между ними, порядком смены состоя­ний и другими особенностями структуры и режимов работы. В соответствии с этими признаками производится классификация счетчиков. Классификация счетчиков по модулю счета. Критерием, по которому различаются счетчики, является модуль счета. Счетчик двоичный (Ксч=2m) считает все возможные числа, которые могут быть представлены m-разрядным двоичным кодом. Недвоичные счетчики (Ксч 2m). Отдельную группу недвоичных счетчиков составляют двоично-десятичные счетчики (Kсч=10m).

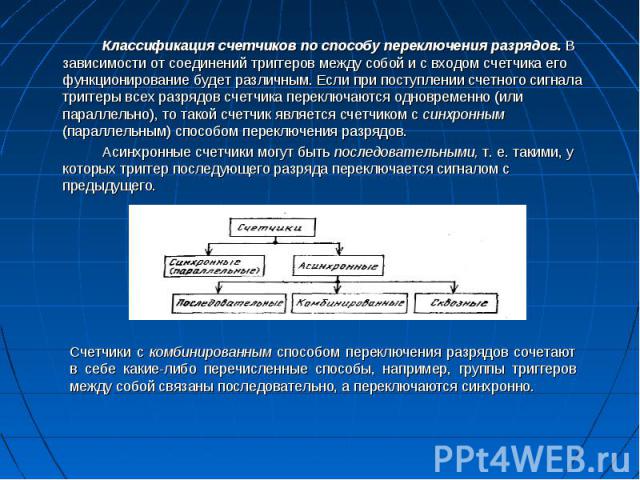
Классификация счетчиков по способу переключения разрядов. В зависимости от соединений триггеров между собой и с входом счетчика его функционирование будет различным. Если при поступлении счетного сигнала триггеры всех разрядов счетчика переключаются одновременно (или параллельно), то такой счетчик является счетчиком с синхронным (параллельным) способом переключения разрядов. Классификация счетчиков по способу переключения разрядов. В зависимости от соединений триггеров между собой и с входом счетчика его функционирование будет различным. Если при поступлении счетного сигнала триггеры всех разрядов счетчика переключаются одновременно (или параллельно), то такой счетчик является счетчиком с синхронным (параллельным) способом переключения разрядов. Асинхронные счетчики могут быть последовательными, т. е. такими, у которых триггер последующего разряда переключается сигналом с предыдущего.

Синхронные двоичные счетчики Количество разрядов счетчика m в общем случае зависит от кода и может быть определено формулой . Скобки означают, что значение логарифма округляется до большего ближайшего целого числа. Для двоичных счетчиков . Рассмотрим пример. Синхронный двоичный суммирующий счетчик, работаю­щий в коде 4–2–1 с модулем счета, равным 8. В данном случае

Схема синхронного двоичного счетчика Схема синхронного двоичного счетчика Уравнения входов младшего разряда имеют максимально простой вид (Jо = Kо =1) и поэтому для их реализации достаточно подключить все входы Jо и Ко триггера к генератору единицы. Входы J1 и K1 триггера первого разряда могут быть подключены двумя способами: соединением всех входов с выходом триггера младшего разряда или соединением одного входа j1 и одного входа К1 к выходу Q0 младшего разряда и подключением всех оставшихся входов к генератору единицы.

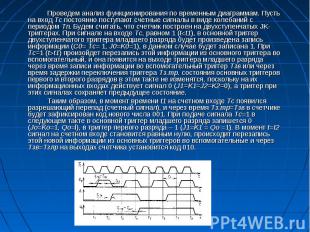
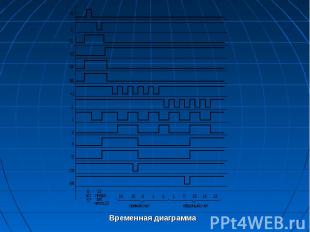
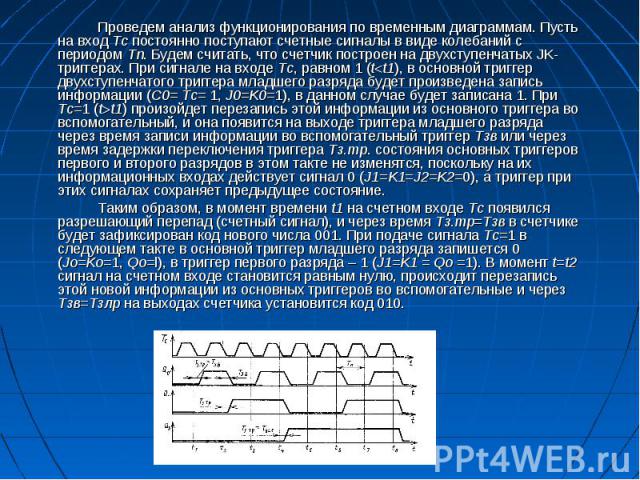
Проведем анализ функционирования по временным диаграммам. Пусть на вход Тс постоянно поступают счетные сигналы в виде колебаний с периодом Тn. Будем считать, что счетчик построен на двухступенчатых JK-триггерах. При сигнале на входе Тс, равном 1 (t t1), в основной триггер двухступенчатого триггера младшего разряда будет произведена запись информации (С0= Тс= 1, J0=K0=1), в данном случае будет записана 1. При Тс=1 (t t1) произойдет перезапись этой информации из основного триггера во вспомогательный, и она появится на выходе триггера младшего разряда через время записи информации во вспомогательный триггер Тзв или через время задержки переключения триггера Тз.тр. состояния основных триггеров первого и второго разрядов в этом такте не изменятся, поскольку на их информационных входах действует сигнал 0 (J1=K1=J2=K2=0), а триггер при этих сигналах сохраняет предыдущее состояние. Проведем анализ функционирования по временным диаграммам. Пусть на вход Тс постоянно поступают счетные сигналы в виде колебаний с периодом Тn. Будем считать, что счетчик построен на двухступенчатых JK-триггерах. При сигнале на входе Тс, равном 1 (t t1), в основной триггер двухступенчатого триггера младшего разряда будет произведена запись информации (С0= Тс= 1, J0=K0=1), в данном случае будет записана 1. При Тс=1 (t t1) произойдет перезапись этой информации из основного триггера во вспомогательный, и она появится на выходе триггера младшего разряда через время записи информации во вспомогательный триггер Тзв или через время задержки переключения триггера Тз.тр. состояния основных триггеров первого и второго разрядов в этом такте не изменятся, поскольку на их информационных входах действует сигнал 0 (J1=K1=J2=K2=0), а триггер при этих сигналах сохраняет предыдущее состояние. Таким образом, в момент времени t1 на счетном входе Тс появился разрешающий перепад (счетный сигнал), и через время Тз.тр=Тзв в счетчике будет зафиксирован код нового числа 001. При подаче сигнала Тс=1 в следующем такте в основной триггер младшего разряда запишется 0 (Jо=Kо=1, Qo=l), в триггер первого разряда – 1 (J1=K1 = Qo =1). В момент t=t2 сигнал на счетном входе становится равным нулю, происходит перезапись этой новой информации из основных триггеров во вспомогательные и через Тзв=Тзлр на выходах счетчика установится код 010.

Реверсивные и асинхронные счетчики. Синхронный двоичный реверсивный счетчик Реверсивный счетчик сочетает в себе свойства суммирующего и вычитающего счетчиков. Реверсивные счетчики строятся двумя способами. В первом случае счетчик имеет один счетный и один управляющий входы, причем в зависимости от сигнала на управляющем входе счетчик работает либо в режиме суммирования, либо в режиме вычитания. Во втором случае счетчик имеет два счетных входа, при подаче счетных сигналов на один из входов они суммируются, при подаче на другой – вычитаются. Минимально возможная длительность Т0min определяется процессом перезаписи информации из основного во вспомогательный триггер Тзв. T1min определяется временем задержки распространения сигнала через дополнительно введенные логические элементы Гз.ср и временем записи информации в основной триггер каждого из разрядов: T1min= Tз.ср+Tзо. Отсюда разрешающее время и максимальная рабочая частота счетчика

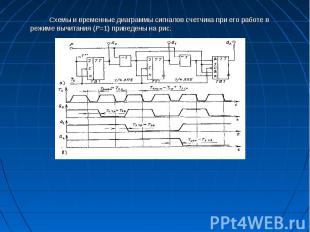
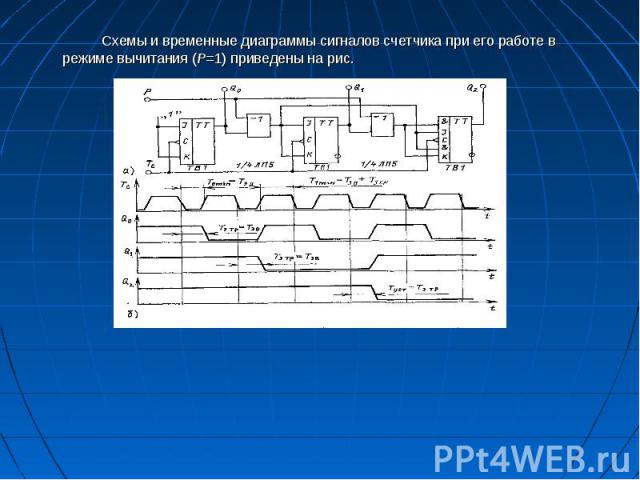
Схемы и временные диаграммы сигналов счетчика при его работе в режиме вычитания (Р=1) приведены на рис. Схемы и временные диаграммы сигналов счетчика при его работе в режиме вычитания (Р=1) приведены на рис.

Асинхронные счетчики Интересны асинхронные счетчики в упрощенном исполнении. Упрощение схемы асинхронного счетчика достигается тем, что разрешающий сигнал поступает на тактовые входы С триггеров не в каждом такте, как в синхронных счетчиках, а по возможности только в те такты, когда триггер должен изменить свое состояние. В остальные такты работы разрешающий сигнал стремятся не подавать, и это позволяет иметь произвольные сигналы на информационных входах триггеров. Асинхронный суммирующий двоичный счетчик

Анализ работы счетчика проведем с использованием временных диаграмм. Анализ работы счетчика проведем с использованием временных диаграмм. При Tс=1 происходит запись информации в основной триггер двухступенчатого триггера младшего разряда. Так как сигнал на его информационных входах всегда равен единице, то в него записывается двоичный сигнал, противоположный сигналу на выходе триггера Q0. Как только сигнал на счетном входе становится равным нулю, начинается процесс перезаписи информации из основного триггера во вспо­могательный, и через время Tзв=Tз.тр на выходах счетчика зафиксируются сигналы Q0 = l, Q1 =Q2 =0. Как видно, при этом переключении новый код (001) счетчика установился через время Tз.тр. Однако это не будет временем установления счетчика в целом. Для его определения необходимо рассмотреть все возможные переключения и выбрать наибольшее. При переключении старшего разряда, для которого тактирующим сигналом является выходной сигнал первого разряда Q1, время установления кода утраивается (ЗTз.тр), это время – наибольшее время переключения, оно и является временем уста­новления кода счетчика

Регистры. Назначение и классификация регистров Регистрами называются цифровые устройства, осуществляющие кратковременное хранение и преобразование многоразрядных двоичных чисел, т.е. они являются оперативными запоминающими устройствами (ОЗУ). В качестве запоминающих элементов в регистрах используются триггеры. Число триггеров, предназначенных для хранения многоразрядного числа, равно количеству разрядов в этом числе. В регистрах используются в качестве вспомогательных элементов комбинационные схемы для осуществления: ввода и вывода из регистра хранимого числа; преобразование кода числа, хранящегося в регистре; сдвига числа в сторону старших или младших разрядов на определенное число разрядов; преобразования последовательного кода числа в параллельный и наоборот и др. Регистры классифицируются по способу ввода информации в регистр и ее вывод. Ввод и вывод информации (двоичных чисел) в параллельных регистрах (регистрах памяти) осуществляется одновременно во всех разрядах (в параллельном коде). При этом время ввода (вывода) информации равно времени ввода (вывода) одного разряда.

Ввод и вывод информации в последовательных регистрах (регистрах сдвига) осуществляется последовательно разряд за разрядом (в последовательном коде). Время ввода (вывода) m-разрядного двоичного числа в регистрах сдвига равно тТСД, где Тся – период следования тактирующих сигналов, осуществляющих ввод (вывод) информации. В комбинированных регистрах ввод числа может осуществляться в параллельном коде, а вывод – в последовательном или наоборот. Ввод и вывод информации в последовательных регистрах (регистрах сдвига) осуществляется последовательно разряд за разрядом (в последовательном коде). Время ввода (вывода) m-разрядного двоичного числа в регистрах сдвига равно тТСД, где Тся – период следования тактирующих сигналов, осуществляющих ввод (вывод) информации. В комбинированных регистрах ввод числа может осуществляться в параллельном коде, а вывод – в последовательном или наоборот. Параллельные регистры. Параллельные регистры осуществляют не только хранение двоичных чисел, но и осуществляют преобразование поразрядно двоичные числа. Примером параллельных регистров могут служить регистры памяти, например на D-триггерах.

Регистр памяти на D-триггерах Регистр памяти на D-триггерах Схема регистра памяти на D-триггерах не имеет элементов ввода информации (вводимое число подается непосредственно на входы триггеров). Кроме этого, использование D-триггеров позволяет записывать число, представленное только в прямом коде, что упрощает сопряжение регистра с источником записываемой информации. Таким образом, использование D-триггеров для построения регистров памяти оказывается предпочтительным.

Регистры сдвига Регистры сдвига Регистры сдвига, в свою очередь, можно классифицировать. Регистры сдвига (последовательные регистры), помимо запоминания многоразрядных двоичных чисел, обеспечивают сдвиг хранимого числа на любое число разрядов. Сдвиг кода числа осуществляется с помощью сдвигающих сигналов Тсл, которые перемещают все разряды кода числа от младших разрядов к старшим (влево) или наоборот (вправо), последовательно переводя каждый триггер регистра в состояние, соответствующее разряду кода на входе данного триггера в момент поступления очередного сигнала Тсл. Регистры сдвига могут быть классифицированы по критерию направления сдвига кодов многоразрядных чисел. Регистры, сдвигающие информацию в сторону старших или младших разрядов, обеспечивают сдвиг только в одну сторону. Реверсивные регистры сдвига могут осуществлять сдвиг в любую сторону в зависимости от специального управляющего сигнала, задающего это направление.

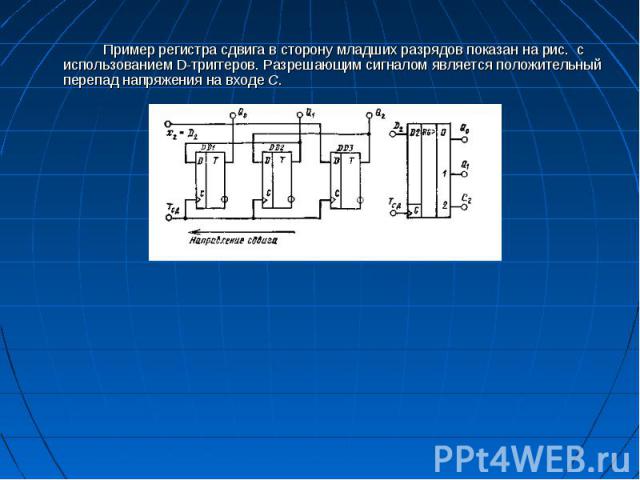
Пример регистра сдвига в сторону младших разрядов показан на рис. с использованием D-триггеров. Разрешающим сигналом является положительный перепад напряжения на входе С. Пример регистра сдвига в сторону младших разрядов показан на рис. с использованием D-триггеров. Разрешающим сигналом является положительный перепад напряжения на входе С.

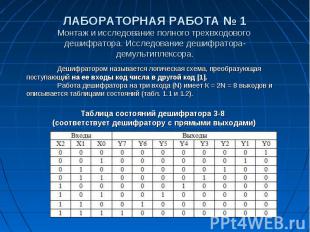
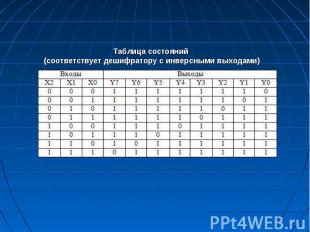
ЛАБОРАТОРНАЯ РАБОТА № 1 Монтаж и исследование полного трехвходового дешифратора. Исследование дешифратора- демультиплексора.

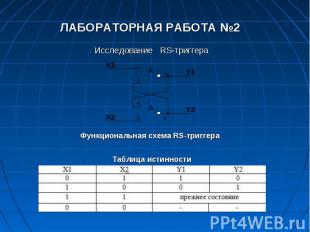
ЛАБОРАТОРНАЯ РАБОТА № 3