Презентация на тему: Решение нестандартных задач

1. решение логических задач становится очень 1. решение логических задач становится очень простым уже в пятом классе. 2.задача №1 о четырех друзьях. 3. решение задачи №1. 4.условие задачи №2 о трех друзьях для самостоятельного решения. 5.проверка решения задачи №2. 6.задача №3 о жидкостях. 7.решение задачи №3. 8.задача №4 про зверей. 9.решение задачи №4. 10.задача№5.о профессиях 11.решение задачи№5. 12.выводы. 13.литература. 14.выход.

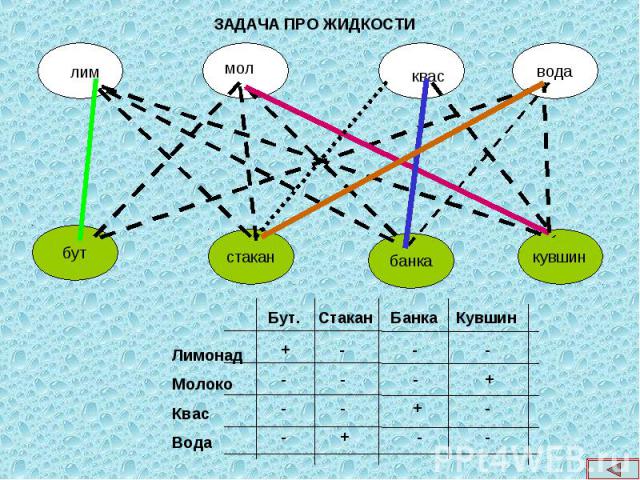
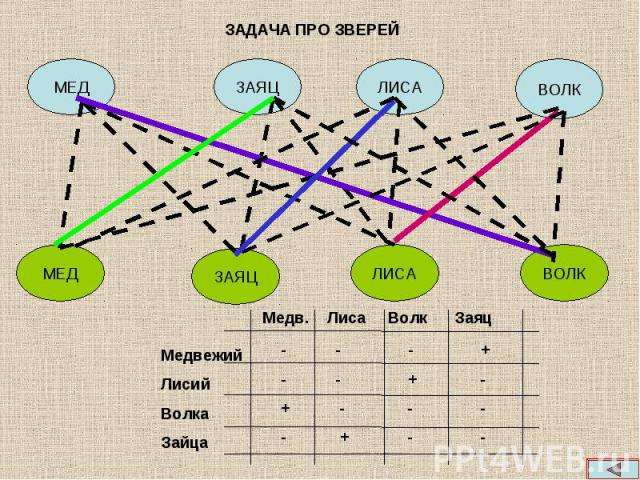
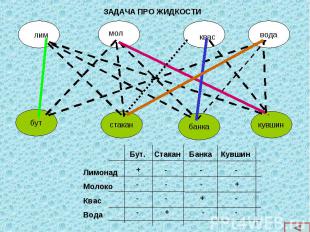
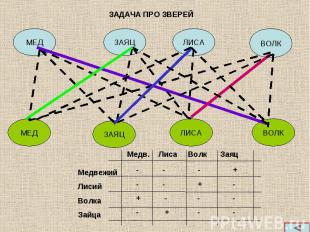
Логические задачи занимают особое место, они носят и занимательный характер и развивают логическое мышление. Я предлагаю один из вариантов методики обучения решению таких задач. Перед началом решения выясняем, что между двумя множествами устанавливается взаимно однозначное соответствие( в предлагаемых задачах). Логические задачи занимают особое место, они носят и занимательный характер и развивают логическое мышление. Я предлагаю один из вариантов методики обучения решению таких задач. Перед началом решения выясняем, что между двумя множествами устанавливается взаимно однозначное соответствие( в предлагаемых задачах). Элементы множеств изображаем друг под другом кругами (все зависит от фантазии учителя).И начинаем устанавливать соответствие. Я их называю прочные и разрывные связи. Читаем условие по одной строке и сразу же изображаем связь. Условие задач нужно читать и анализировать порциями, которые выделены в слайдах отдельными частями. При желании текст можно вывести на бумагу для более удобного анализа.

В одном дворе живут четыре друга. В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, Электрик-младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

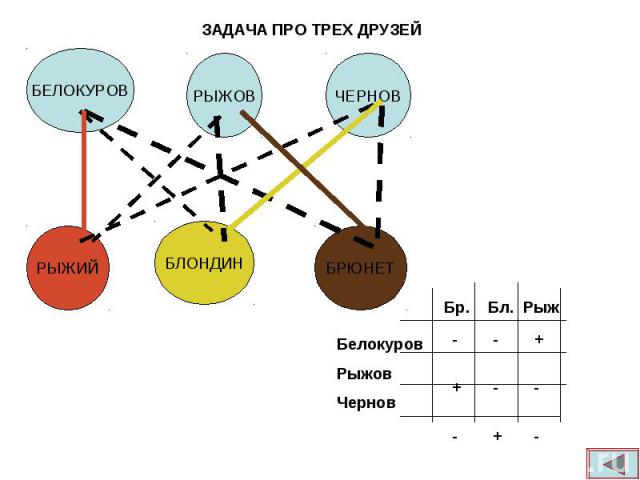
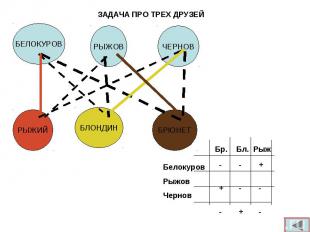
Беседуют трое друзей: Белокуров , Рыжов и Чернов. Беседуют трое друзей: Белокуров , Рыжов и Чернов. Брюнет сказал Белокурову : "Любопытно , что один из нас блондин , другой- брюнет, третий-рыжий, но ни у кого цвет волос не соответствует фамилии". Какой цвет волос у каждого из друзей? Условие задачи и один из вариантов решения (табличный) можно посмотреть в приложении "Математика" №7 за 2005год

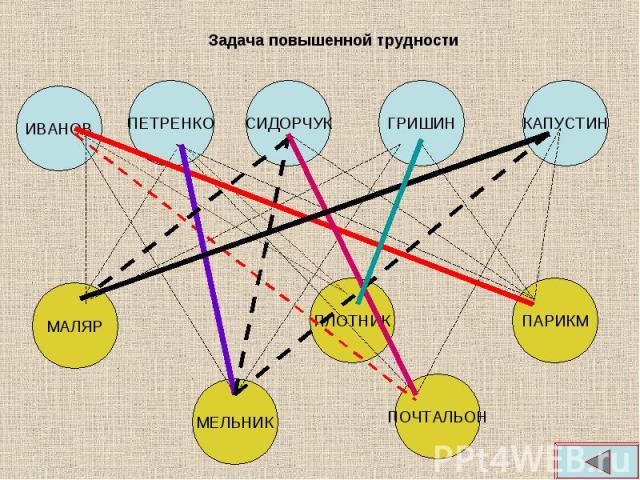
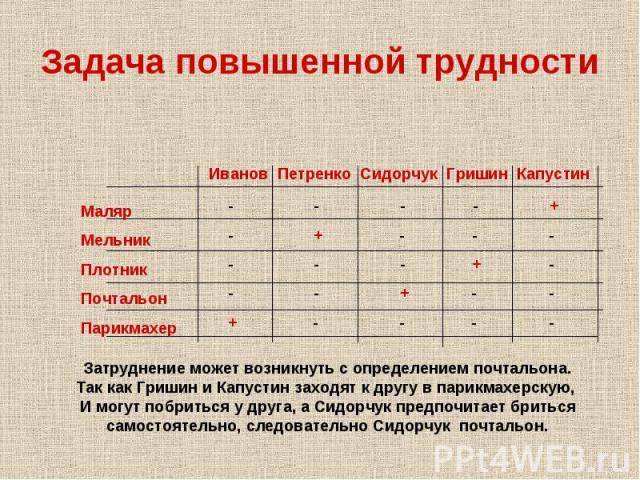
В небольшом городке живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. В небольшом городке живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные: один из них маляр, другой- мельник, третий- плотник, четвертый-почтальон, а пятый- парикмахер. Петренко и Гришин никогда не держали в руках малярной кисти. Иванов и Гришин собираются посетить мельницу, на которой работает их товарищ. Петренко и Капустин живут в одном доме с почтальоном. Сидорчук был недавно в ЗАГСе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком. Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром. Гришин и Капустин по субботам обязательно встречаются в парикмахерской, где работает их друг. Почтальон предпочитает бриться сам. Кто есть кто?

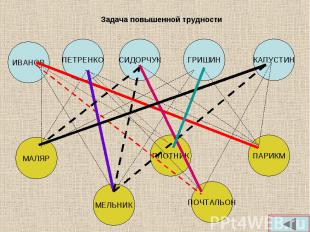
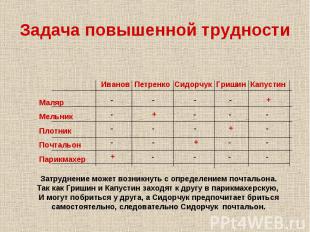
Предлагаемые два варианта решения логических задач является распространенными, и вы можете выбрать удобный для Вас способ решения. Предлагаемые два варианта решения логических задач является распространенными, и вы можете выбрать удобный для Вас способ решения.

1.Т.Д.Гаврилова.Занимательная математика.5-11классы. (Волгоград.2003г) 1.Т.Д.Гаврилова.Занимательная математика.5-11классы. (Волгоград.2003г) 2."Математика"-приложение к газете "Первое сентября" №7,2005г 3. "Математика" №10.2005г