Презентация на тему: Место математики в изучении акустических характеристик слуховых аппаратов

Место математики в изучении акустических характеристик слуховых аппаратов

Цель работы Определить значение математики в изучении акустических характеристик слуховых аппаратов

Задачи исследования определить актуальность выбранной темы;узнать роль математики в медицине;подробно рассмотреть акустические характеристики ушных вкладышей;составит понятийный аппарат незнакомых терминов.

выполнить задачи работы, проанализировать её;подвести итоги и сделать выводы;предоставить исследование научной комиссии;выполнить рефлексию проделанного труда.

В настоящее время все большее внимание уделяется проблеме слуха. Существуют различные взгляды на определение причин нарушений слуха:факторы наследственного характера;факторы эндо- или экзогенного воздействия на орган слуха.

Роль математики велика и в музыке, и в медицине, и в образовании. Но более подробно хочется рассмотреть её роль в медицине, а именно в изучении акустических характеристик слуховых аппаратов. Данная тема позволила разобраться в практической пользе математики, например, с помощью математических расчетов создаются инновационные виды слуховых аппаратов.

Слух – важнейшее из человеческих чувств, оказывающий влияние на формирование и развитие личностных качеств членов общества, в той или иной мере, влияющий на развитие интеллекта и профессиональных способностей каждого человека. Как же математика – «царица всех наук» - помогает решать данные вопросы о причинах возникновения и методах лечения нарушения слуха?

математика служит основой для моделирования в обработке изображений;математика с её обширным репертуаром методов научных вычислений позволяет эффективную реализацию модели на современных технических средствах;математика дает теоретический инструмент для понимания и анализа моделей медицины.

Исторически первыми слуховыми аппаратами были слуховые трубы – рупоры из различных материалов .В 1878 г. был сконструирован первый электрический слуховой аппарат.В 1990-х появились цифровые слуховые аппараты.

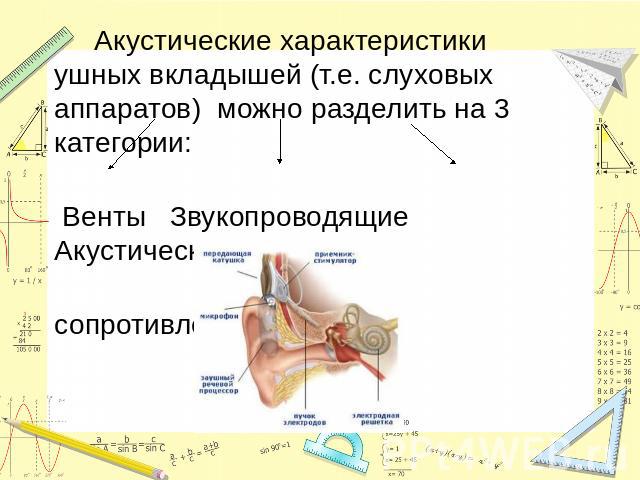
Акустические характеристики ушных вкладышей (т.е. слуховых аппаратов) можно разделить на 3 категории: Венты Звукопроводящие Акустическое трубочки сопротивление

Венты снижают усиление низкочастотных звуков, проявляя свой наибольший эффект ниже 1000 Гц. Масса воздуха, пойманная в «ловушку» внутри вента, действует как акустическая инерционная масса. Воздушная масса колеблется в качестве единого целого и создает резонанс в районе 400-500 Гц, что несколько ослабляет эффект вента, усиливая звуки в этом диапазоне.

Чтобы запомнить об ослаблении эффекта вента под влиянием воздуха, следует пользоваться формулой: F=5500Hz √ (πr²/Io-Ve) Умножить 5500 Гц на квадратный корень поперечной площади вента в кв.см (πr²), деленный на длину вента (Io) и объем воздуха (Ve)

Резонансная частота воздуха, пойманного в ловушку внутри вента, прямо пропорциональна его длине. Длинный и узкий вент будет иметь относительно низкий частотный резонанс, в то время как короткий и широкий вент будет иметь более высокий частотный резонанс.

Низкий и высокий частотный резонансНизкий Высокий

Слуховой аппарат с длинным узким вентом будет иметь резонанс на частоте 300-400 Гц, и это приведёт к тому, что собственный голос человека будет странно звучать, то есть произойдёт эффект окклюзии = > короткие широкие венты будут лучше снижать эффект окклюзии.

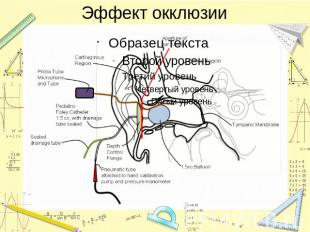
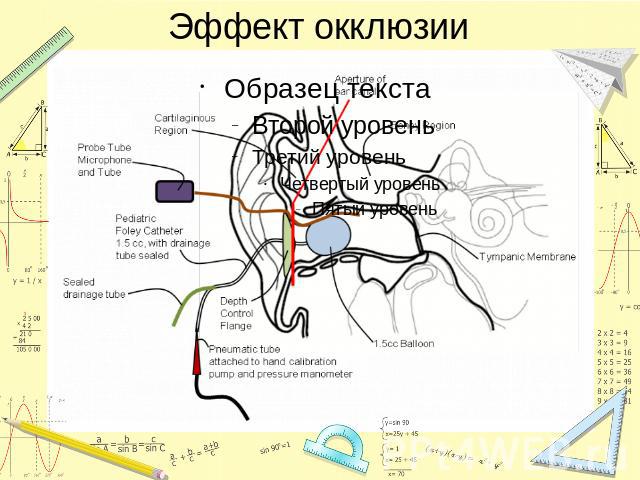
Эффект окклюзии

Резонансная частота варьируется в зависимости от квадратного корня, поэтому нужно менять как диаметр, так и длину вента. Изменения под знаком корня приведут к меньшим изменениям акустических характеристик, нежели если бы изменения проводились без извлечения корня. То же самое относится и к логарифмам.

Вент будет оказывать влияние на реальный коэффициент компрессии при настройке средств защиты слуха (СА). В случае большого вента низкочастотный звук будет поступать в ухо напрямую, минуя слуховой аппарат, и будет суммироваться с низкочастотным выходным сигналом СА низкой интенсивности, тем самым повышая крутизну функции вход/выход слухового вкладыша для негромких входных сигналов. Физические законы компрессии

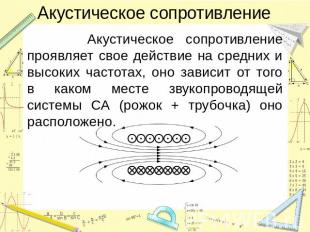
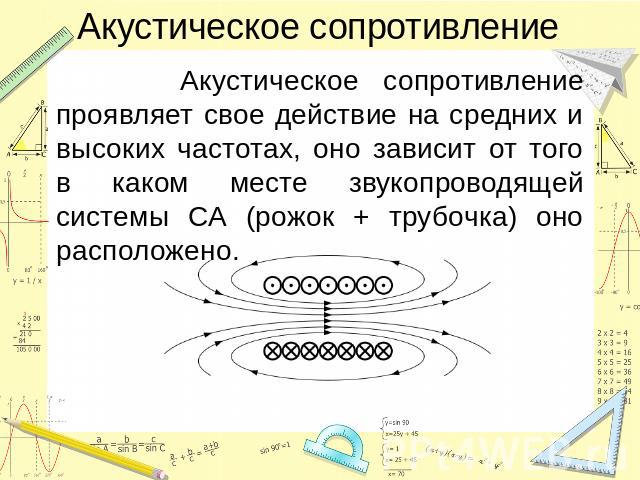
Акустическое сопротивление проявляет свое действие на средних и высоких частотах, оно зависит от того в каком месте звукопроводящей системы СА (рожок + трубочка) оно расположено. Акустическое сопротивление

Акустическая волна, которая распространяется по любой трубе, зависит от ее граничных условий и определяется длиной трубы, а не поперечным сечением. (Труба должна быть открыта с одного конца и закрыта с другого – это рождает четвертьволновые резонаторы).

F= v/4L Резонансы звукопроводящей трубочки управляются скоростью звука “v”, делённой на длину трубочки “L”, умноженную на четыре. Пример: длина трубочки равна 75 мм; скорость звука равна 340 м/с (340 000 мм/с); F=340 000 мм/с:4*75 = 340 000 / 300 = =1100 Гц ≈ 1000 Гц – это резонанс Резонанс 1000 Гц имеет «друзей» на повторяющихся нечетных числах 3000 Гц и 5000 Гц.

Удельный импеданс трубочки определяется согласно формуле: Удельный импеданс = 41 Ом Площадь поперечного сечения (см)² Акустическое сопротивление вряд ли будет нужно для тонких трубочек , потому что они в большинстве случаев используются для протезирования, оставляющее ухо открытым.

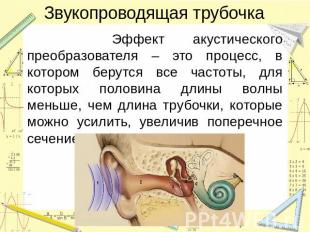
Эффект акустического преобразователя – это процесс, в котором берутся все частоты, для которых половина длины волны меньше, чем длина трубочки, которые можно усилить, увеличив поперечное сечение трубочки.

Если трубочка постепенно расширяется, и диаметр этого раструба составляет не менее ⅓ от общей длины трубки, то это будет усиливать интенсивность высокочастотных компонентов звука.

Формула эффекта акустического преобразователя: F= v / 2L Эта формула поможет найти частоту, начиная с которой трубочка с эффектом горна будет проявлять своё действие.Пример: Длина трубочки СА (L)=75 мм; Скорость звука (v) = 340 000 мм/с; F = 340 000 мм/с : (2*75 мм) = 2200 Гц;

Формула, позволяющая рассчитать эффект горна: Фактор усиления (дБ) = 20 log*(диаметр 2 /диаметр 1)Пример: Внутренний диаметр трубочки = =2 мм; Внешний диаметр = 4 мм; 20 log (4/2) = 20 log2 = 6 дБ

Почему нельзя увеличить электрическое усиление на 6дБ на высоких частотах? Ответ: Можно, но это сократит срок службы батарейки в СА. Если внутренний диаметр удваивается, то усиление на 6 дБ возникает на высоких частотах независимо от первоначального диаметра трубочки! Пример: 20 log (2/1) = 20 log2 = 6 дБ; 20 log (6/3) = 20 log2 = 6 дБ.

1. Акустические характеристики 2. акустическое сопротивление 3. венты 4. звукопроводящие трубочки 5. компрессия 6. резонанс 7. резонаторы 8. слуховой аппарат 9. удельный импеданс 10. эффект акустического преобразователя 11. эффект горна 12. эффект окклюзии

Чтобы на практике убедиться во всей важности математики в создании слуховых аппаратов и изучении акустики, я посетила Сургутский центр слуха и слухопротезирования «Аудиофон». Аминева О.В. – директор данного центра и специалист-сурдолог помогла дополнить данную научно-исследовательскую работу практическим и теоретическим материалом.

В ходе исследовательской работы была определена роль математики в изучении акустических характеристик слуховых аппаратов. С помощью геометрии, алгебры и физических законов проводятся испытания слуховых аппаратов. Таким образом, методы акустики позволяют человеку слышать определённую громкость, тембр, темп и диапазон речи.

1. Гусева Е.Е., Дзюбук Н.А., Константинова М.А., Ласкина М.В., Шиханова Я.В. – газета «Радуга звуков» №4 (40) – декабрь 2010;2. М. Чейсин – журнал «The Hearing Review» № 11 – ноябрь 2009;3. www.krainamriv.org <26.02.2012>;4. www.audiofon.org <10.04.2012>;5. http://radioskot.ru/publ/prostoj_sluxovoj_apparat/1-1-0-244 <11.04.2012>;6. articlehost.ru/article/a-244.html <13.04.2012>;7. www.nvsaratov.ru/nvrubr/ELEMENT_ID=9503 <13.04.2012>