Презентация на тему: Арккосинус и решение уравнения cos x = a

Арккосинус и решение уравнения cos x = a Уроки № 1-2

Цели урока ввести понятие arccos x; вывести формулу решения уравнения cos x=a, ; рассмотреть уравнения на применение этой формулы; рассмотреть простейшие тригонометрические неравенства.

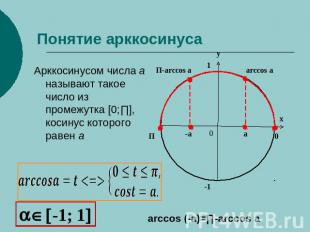
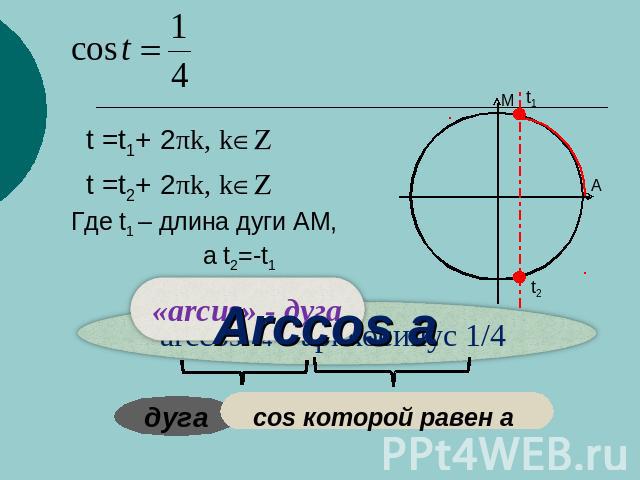
Понятие арккосинуса Арккосинусом числа а называют такое число из промежутка [0;∏], косинус которого равен а

Имеют смысл выражения?

Для чего нужен арккосинус?

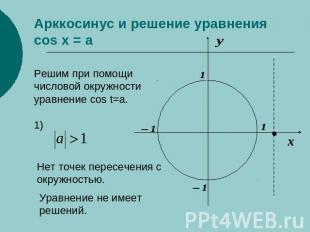
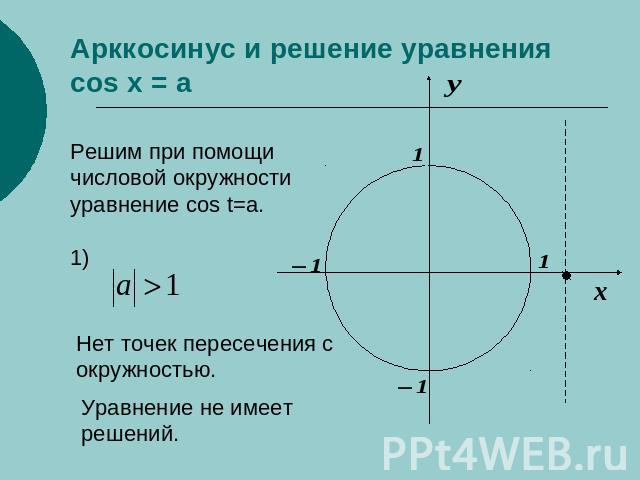
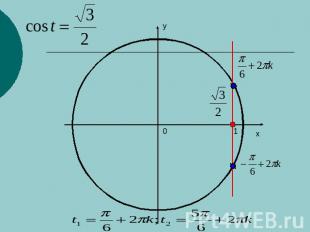
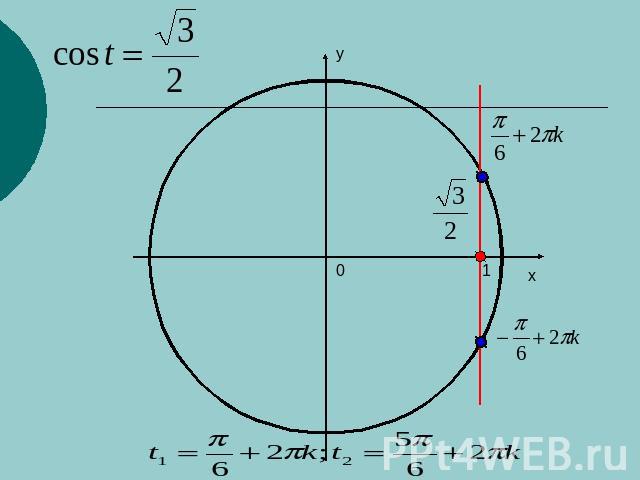
Арккосинус и решение уравнения cos x = a Решим при помощичисловой окружностиуравнение cos t=a.1)Нет точек пересечения с окружностью.Уравнение не имеет решений.

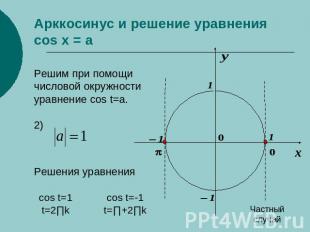
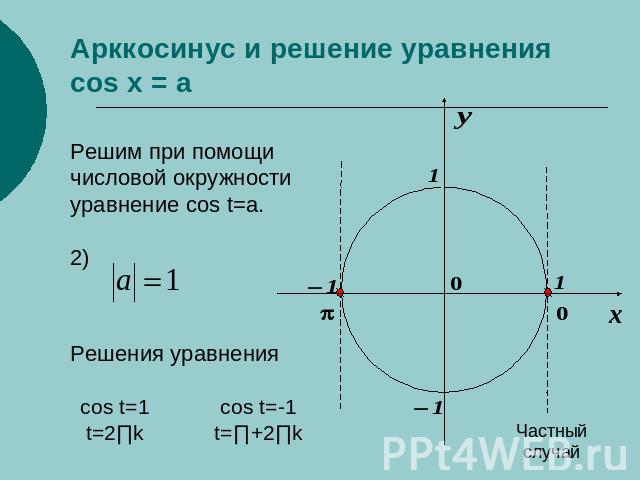
Арккосинус и решение уравнения cos x = a Решим при помощичисловой окружностиуравнение cos t=a.2)

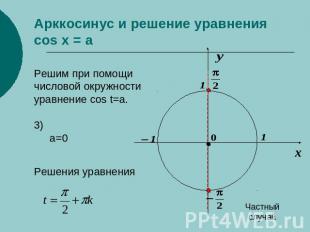
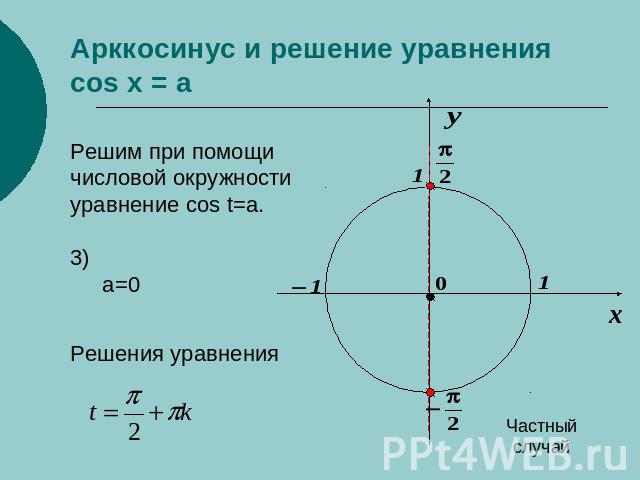
Арккосинус и решение уравнения cos x = a Решим при помощичисловой окружностиуравнение cos t=a.3)

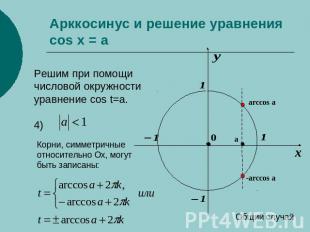
Арккосинус и решение уравнения cos x = a Решим при помощичисловой окружностиуравнение cos t=a.4) Корни, симметричные относительно Оx, могут быть записаны:

Арккосинус и решение уравнения cos x = a

Выясните, верно ли равенство?

Какие из чисел являются арккосинусами?

Основная задача – свести любое тригонометрические уравнение к простейшему виду

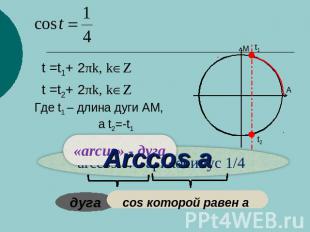
Пример решения уравнения Это частный вид уравнения cos t=a, где a=0

Характерная грубая ошибка Учащиеся делят обе части на 4 и получают следующее:

Пример решения уравнения

Пример решения уравнения

Закрепление изученного материала № 289-291 (а, б) № 293 а, б № 294 а, б

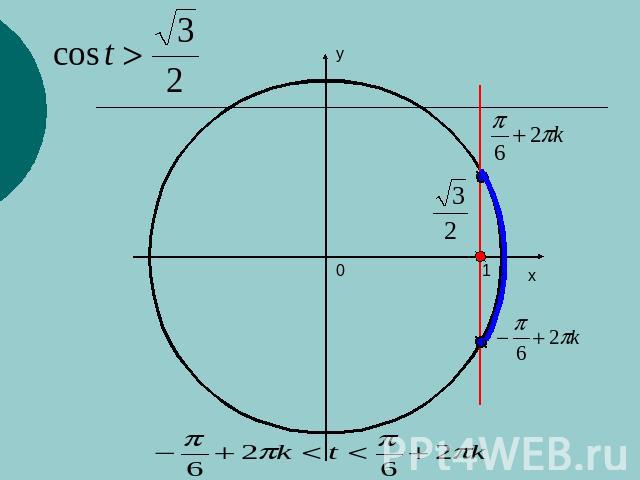
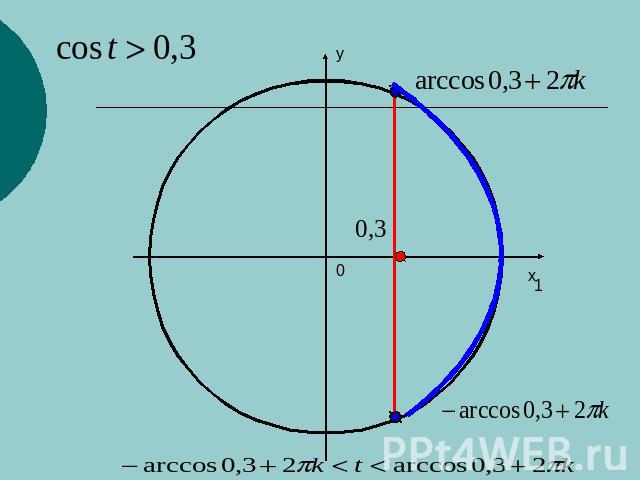
Решение простейших тригонометрических неравенств

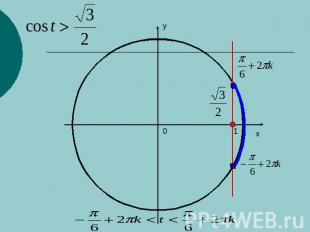
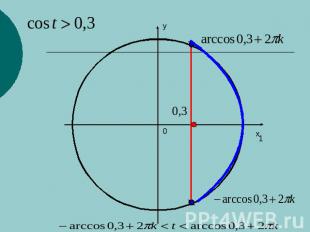
Закрепление изученного материала №303 (а, г) № 304 (а, г)№ 305 (а, г), № 306 (а, г).

Домашнее задание Теория: стр. 75-81№ 291 (в, г) № 293 (в, г) № 294 (в, г) №303 (б, в) № 304 (б, в) № 305 (б, в) № 306 (б, в)