Презентация на тему: Алгоритмы внутренних точек с приближенным решением вспомогательной задачи

Алгоритмы внутренних точекс приближенным решениемвспомогательной задачи Филатов А.Ю.к.ф.-м.н., ИСЭМ СО РАН, ИГУ (Иркутск)Пержабинский С.М.ИСЭМ СО РАН (Иркутск)http://polnolunie.baikal.ru/me/mat_prog.htm,http://matec.isu.ruРабота выполнена при финансовой поддержке РФФИ(проект 05-01-00587а)

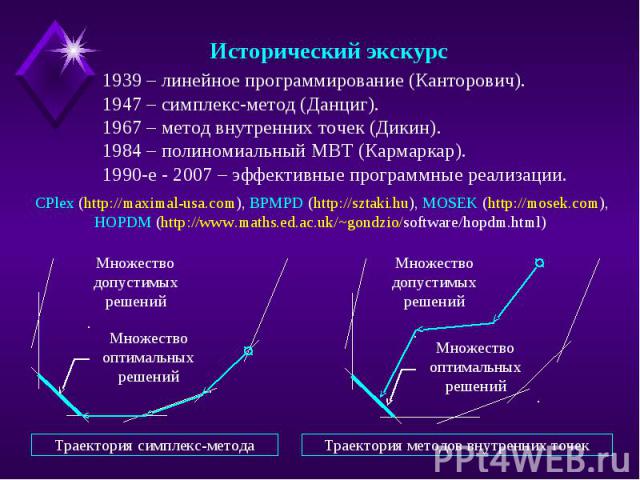
Исторический экскурс 1939 – линейное программирование (Канторович).1947 – симплекс-метод (Данциг).1967 – метод внутренних точек (Дикин).1984 – полиномиальный МВТ (Кармаркар).1990-е - 2007 – эффективные программные реализации. CPlex (http://maximal-usa.com), BPMPD (http://sztaki.hu), MOSEK (http://mosek.com), HOPDM (http://www.maths.ed.ac.uk/~gondzio/software/hopdm.html)

Пара взаимно-двойственных задачлинейного программированияОсновные классы алгоритмоввнутренних точек Аффинно-масштабирующие алгоритмы. Алгоритмы центрального пути. Алгоритмы скошенного пути. Комбинированные алгоритмы. Прямые алгоритмы. Двойственные алгоритмы. Прямо-двойственные алгоритмы.

Аффинно-масштабирующиеалгоритмы внутренних точекСтартовое приближение:Итеративный переход:Задача поиска направления корректировки:Шаг корректировки:Способы выбора весовых коэффициентов:

Алгоритмы центрального пути(имеют полиномиальные оценки)Логарифмическая барьерная функция:Задача поиска направления корректировки:Комбинированные алгоритмы(используют параметризацию)Задача поиска направления корректировки:

Решение вспомогательной задачиАффинно-масштабирующие алгоритмы:Алгоритмы центрального пути:Комбинированные алгоритмы:

Методы решениявспомогательной задачи Метод Гаусса. Метод Халецкого (метод квадратного корня). Метод сопряженных направлений. Метод Зейделя. Другие приближенные итеративные методы.Предпосылки использованияприближенных итеративных методов На первых итерациях достаточно искать приближенное направление корректировки , используя вектор , для которого . В финале вычислительного процесса, диагональная мат- рица изменяется по итерациям очень незначительно, имеется хорошее стартовое приближение .

Метод сопряженных направленийИтеративный переход:Направление корректировки:Шаг, определяющий вариант метода:Шаг корректировки:

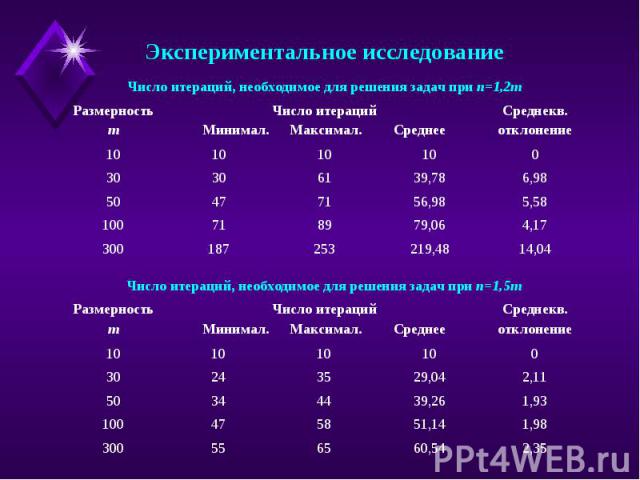
Экспериментальное исследование Число итераций, необходимое для решения задач при n=1,2mЧисло итераций, необходимое для решения задач при n=1,5m

Параметры управления алгоритмом Вариант приближенного метода. – параметр в условии останова δ – параметр в условие перехода с точного на приближенный метод K – максимальное число выполняемых подряд итераций приближенного метода. t – число внутренних итераций приближенного метода. Процедуры корректировки формул (3), (10) и формул вычисления максимального шага на фазе 1.

Спасибоза внимание!