Презентация на тему: Решение СЛАУ в EXEL

Решение системы уравнений в Excel методом Крамера и обратной матрицы

Метод Крамера Ме тод Кра мера — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно). Для системы n линейных уравнений с n неизвестными - основная матрица системы.

Определитель квадратной матрицы  равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения - определитель системы: Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Нахождения неизвестных переменных по методу Крамера 

Метод обратной матрицы Ма тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит следующем . Пусть дана система линейных уравнений с  неизвестными (над произвольным полем): Тогда её можно переписать в матричной форме: А*X=B, где А- основная матрица системы; B и X - столбцы свободных членов и решений системы соответственно:

Найдём обратную матрицу по формуле: Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле    

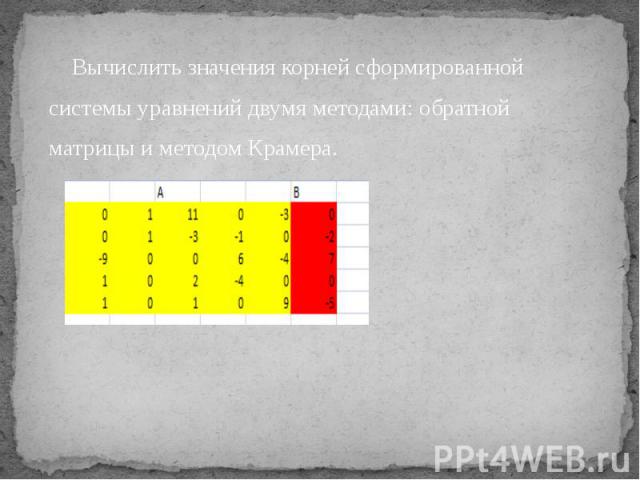
Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.

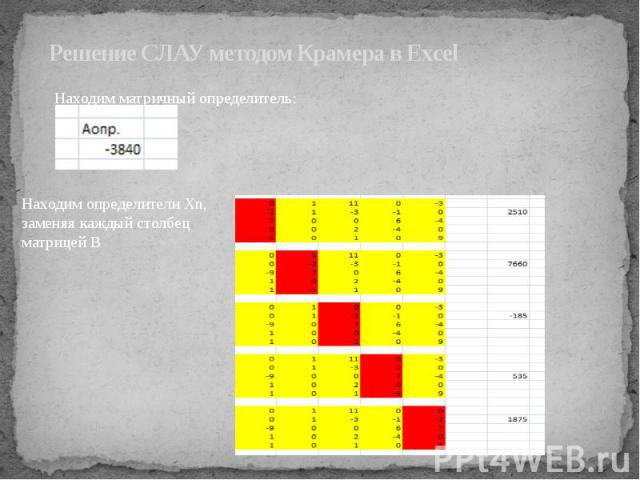
Решение СЛАУ методом Крамера в Excel

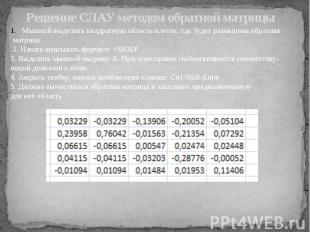
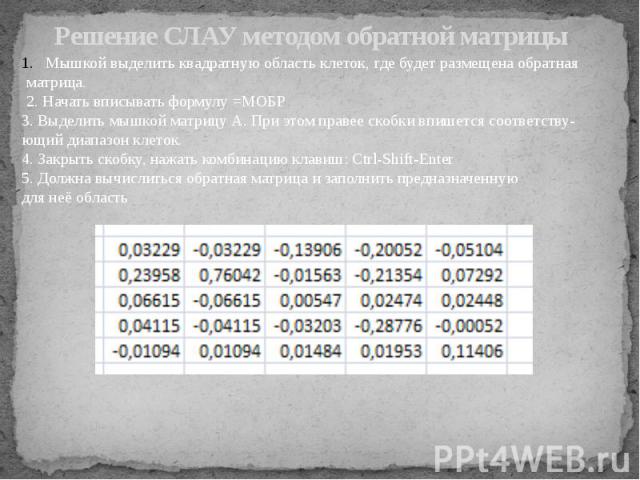
Решение СЛАУ методом обратной матрицы

1.Начать вписывать формулу =МУМНОЖ 2.Выделить мышкой матрицу - первый сомножитель. 3. Выделить мышкой вектор- второй сомножитель. 4.нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Вычислиться произведение и заполниться предназначенная для неё область.