Презентация на тему: Понятие «информация» и свойства информации

Понятие «информация» и свойства информации

«Информация» - от лат. Informatio означает сведение, разъяснение, ознакомление.В биологии понятие «информация» связывается с целесообразным поведением живых организмов.В физике информация рассматривается как антиэнтропия или энтропия с обратным знаком.В кибернетике понятие «информация» связано с процессами управления в сложных системах, живых организмах или технических устройствах.С точки зрения процесса познания информация может рассматриваться как знания.

Социально значимые свойства информации:понятность;полезность;достоверность;актуальность точность;полнота.

Единицы измерения информации За единицу количества информации принимается количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица называется «бит», а следующей по величине единицей является байт:1 байт = 23 бит = 8 бит

Кратные байту единицы измерения:1 Кбайт = 210 байт = 1024 байт;1 Мбайт = 210 Кбайт = 1024 Кбайт;1 Гбайт = 210 Мбайт = 1024 МбайтСуществует формула, связывающая между собой количество возможных событий N и количество информации I: N=2I

Пример: В игре «крестики – нолики» на поле 8х8 перед первым ходом существует 64 возможных события (64 различных варианта расположения «крестика»), тогда уравнение принимает вид: 64 = 2I. Так как 64 = 26, то получим 26=2I. Таким образом, I = 6 битов, т.е.количество информации, полученное вторым игроком после первого хода первого игрока, составляет 6 битов.Задание 2.1Какое количество информации получит второй игрок после первого хода первого игрока в игре в «Крестики – нолики» на поле размером 4х4?

Алфавитный подход к определению количества информации.Формула Шеннона.

Количество информации, которое содержит сообщение закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на количество знаков. В русском алфавите, если не использовать букву Ё, количество событий (букв) будет равно 32. Тогда: 32= 2I, откуда I = 5, т.е. каждый символ несет 5 битов информации.

Формулу для вычисления количества информации в случае различных вероятностей событий предложил К.Шеннон в 1948 году:где I -количество информации;N - количество возможных событий;Pi – вероятность i-го события

Этот подход к определению количества информации называется вероятностным. Когда события равновероятны (Pi=1/N), величину количества информации I можно рассчитать по формуле:Количество информации, которое мы получаем, достигает максимального значения, если события равновероятны.

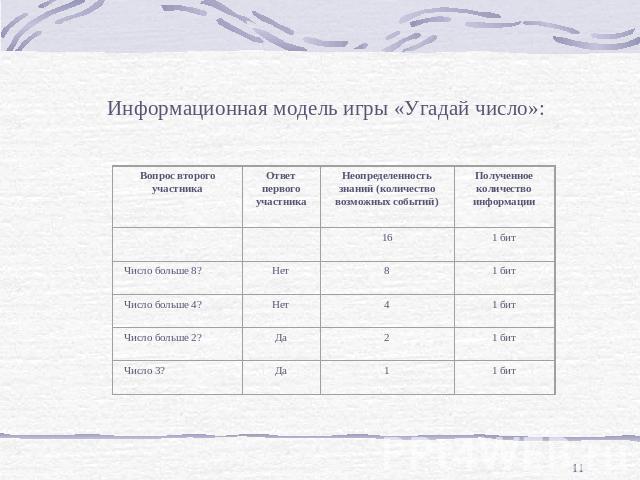
Информационная модель игры «Угадай число»: