Презентация на тему: Задачи оптимизации

Задачи оптимизации Среди прикладных задач, решаемых с помощью математики, выделяются, так называемые, задачи оптимизации. Среди них:транспортная задача о составлении оптимального способа перевозок грузов;задача о диете, т.е. о составлении наиболее экономного рациона питания, удовлетворяющего определенным медицинским требованиям;задача составления оптимального плана производства;задача рационального использования посевных площадей и т.д.Несмотря на различные содержательные ситуации в этих задачах, математические модели, их описывающие, имеют много общего, и все они решаются одним и тем же методом, разработанным отечественным математиком Л.В. Канторовичем (1912-1986).В качестве примера задачи оптимизации рассмотрим упрощенный вариант транспортной задачи.

Задача Пусть на четыре завода З1, З2, З3, З4 требуется завезти сырье одинакового вида, которое хранится на двух складах С1, С2. Потребность данных заводов в сырье каждого вида указана в таблице 1, а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок, т. е. такой, при котором общее число тонно-километров наименьшее.

Решение Для решения этой задачи, в первую очередь, проанализируем ее условие и переведем его на язык математики, т. е. составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y и z соответственно. Тогда на четвертый завод с этого склада нужно будет перевезти 20 - x – y - z сырья в тоннах, а со второго склада нужно будет перевезти соответственно 8 - x, 10 - y, 12 - z, x + y + z - 5 сырья в тоннах. Запишем эти данные в таблицу 3.

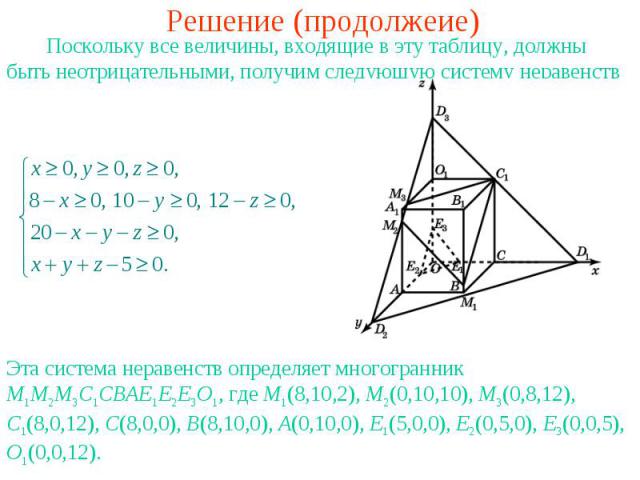
Решение (продолжеие) Поскольку все величины, входящие в эту таблицу, должны быть неотрицательными, получим следующую систему неравенствЭта система неравенств определяет многогранник M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12).

Решение (продолжение)Общее число тонно-километров выражается формулой: 5x + 6y + 4z + 10(20 - x - y - z) + 3(8 - x) + 7(10 - y) + 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.Таким образом, задача сводится к отысканию наименьшего значения функции F = 295 - x - 4y - 2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.Для нахождения наибольшего значения линейной функции на многограннике, достаточно вычислить значения функции в вершинах многогранника и выбрать из них наибольшее. Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограничений: f(M1) = 52, f(M2) = 60, f(M3) = 56, f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24. Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точке M2(0,10,10).

ОтветТаким образом, наиболее выгодный вариант перевозок задается таблицей 4.Таблица 4Заметим, что число независимых переменных в этой задаче было равно трем и поэтому в процессе ее решения получился многогранник. Если бы число независимых переменных равнялось двум, то получился бы многоугольник. В реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются электронно-вычислительные машины.

Упражнение 1 Какая фигура является графиком линейной функции z = ax + by + c?

Упражнение 2 Как расположен график линейной функции z = ax + c по отношению к оси Oy?

Упражнение 3 Как расположен график линейной функции z = ax + by по отношению к началу координат?

Упражнение 4 Что произойдет с графиком линейной функции z = ax + by + c, если c: а) увеличить на единицу; б) уменьшить на единицу?

Упражнение 5 Пусть математическая модель некоторой задачи представляется следующей системой ограничений На множестве решений этой системы найдите наименьшее значение функции F = y - x.

Упражнение 6 На трех складах хранится сырье одинакового вида в количествах соответственно 10 т, 20 т, 30 т. На завод нужно завезти 35 т сырья. Найдите наиболее выгодный вариант перевозок, если расстояния от складов до завода равны 7 км, 5 км, 8 км.

Упражнение 7 Решите предыдущую задачу при дополнительном требовании: со второго склада вывозится сырья не больше, чем с третьего.

Упражнение 8 Установка собирается из трех различных деталей А, Б, В. На одном станке можно за смену изготовить либо 12 деталей типа А, 18 типа Б и 30 типа В (первый режим), либо 20 деталей типа А, 15 типа Б и 9 типа В (второй режим). Хватит ли ста станков, чтобы изготовить за смену детали для 720 установок? Какое наименьшее число станков (и с какими режимами работы) нужно для выполнения заказа?Ответ: Хватит. Наименьшее число станков равно 44, из них 20 должны работать в первом режиме.