Презентация на тему: Описанная и вписанная окружность
Вписанная и описанная окружности 8 класс Мухина Г.Г. – учитель математики МАОУ многопрофильного лицея №20 города Ульяновска.
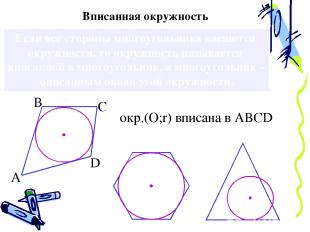
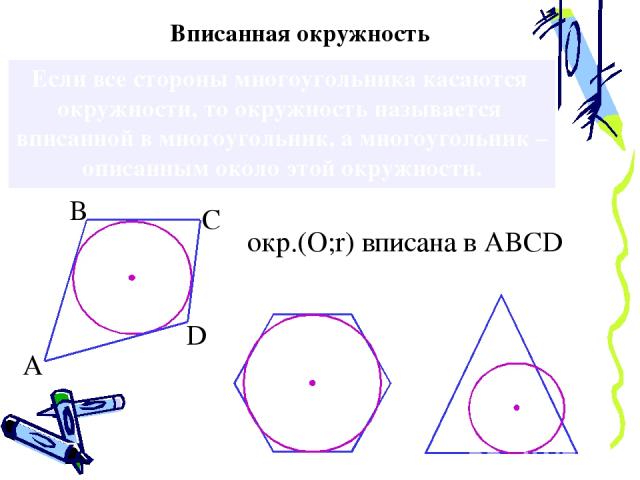
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности. Вписанная окружность А В С D окр.(О;r) вписана в ABCD
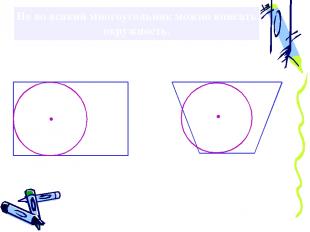
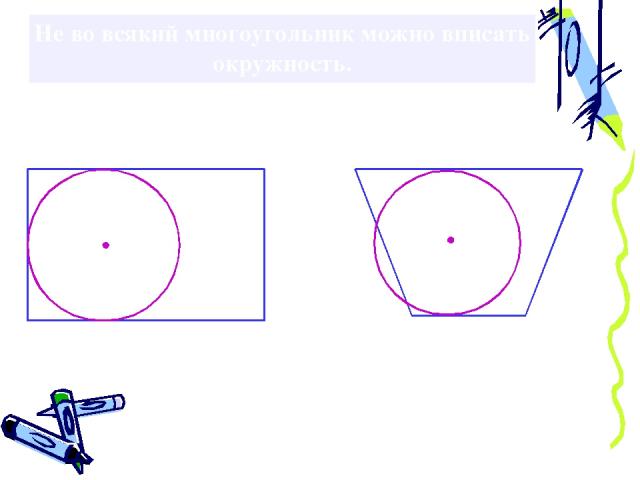
Не во всякий многоугольник можно вписать окружность.
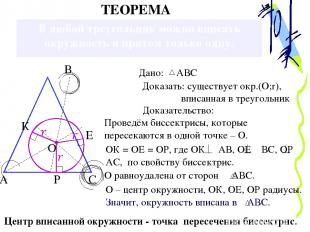
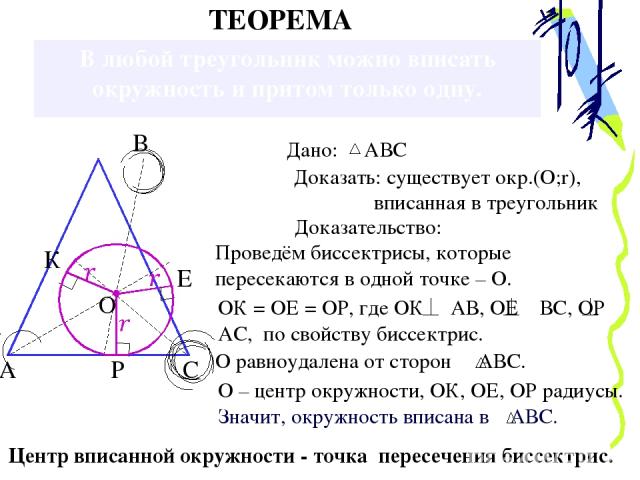
В любой треугольник можно вписать окружность и притом только одну. А Доказать: существует окр.(О;r), вписанная в треугольник Доказательство: Проведём биссектрисы, которые пересекаются в одной точке – О. ОК = ОЕ = ОР, где ОК АВ, ОЕ ВС, ОР АС, по свойству биссектрис. О – центр окружности, ОК, ОЕ, ОР радиусы. ТЕОРЕМА В С О К Е Р Центр вписанной окружности - точка пересечения биссектрис. Дано: АВС Значит, окружность вписана в АВС. О равноудалена от сторон АВС.

Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. А Площадь треугольника В С О
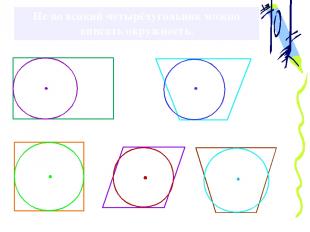
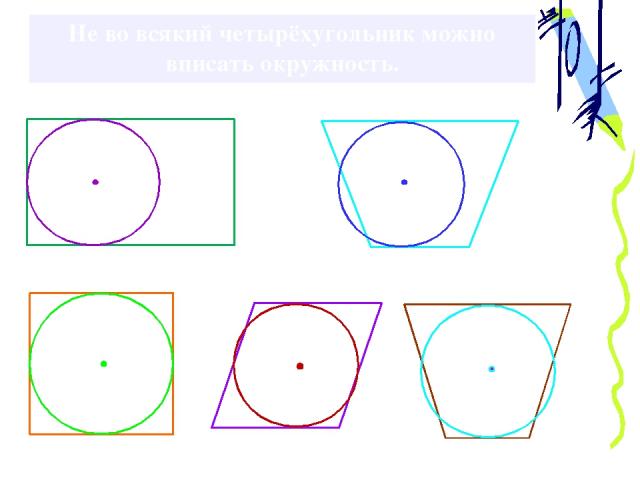
Не во всякий четырёхугольник можно вписать окружность.
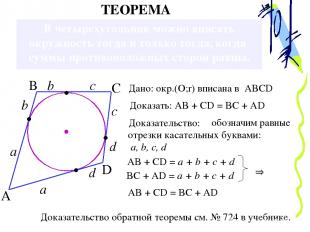
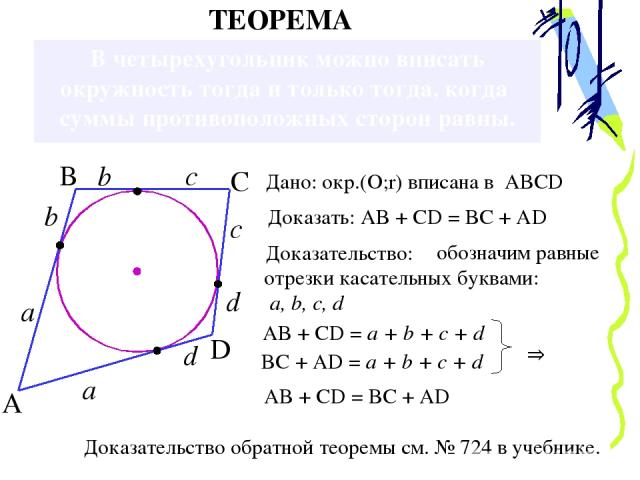
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны. ТЕОРЕМА А В С D Дано: окр.(О;r) вписана в ABCD Доказательство: Доказать: AB + CD = BC + AD a a b b c c d d AB + CD = a + b + c + d BC + AD = a + b + c + d AB + CD = BC + AD Доказательство обратной теоремы см. № 724 в учебнике. обозначим равные отрезки касательных буквами: а, b, c, d

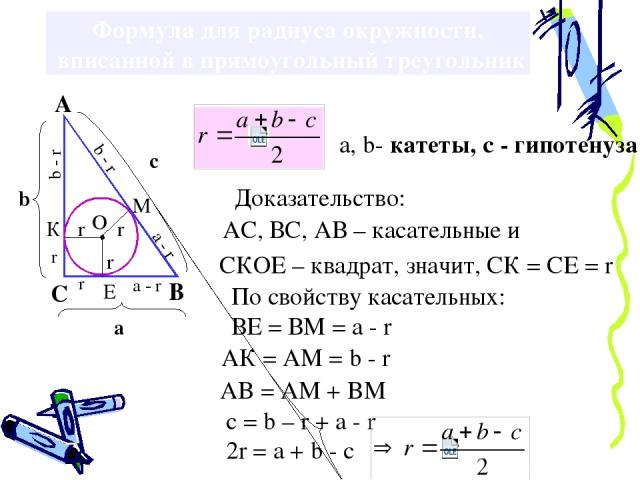
Формула для радиуса окружности, вписанной в прямоугольный треугольник Доказательство: СКОЕ – квадрат, значит, СК = СЕ = r По свойству касательных: ВЕ = ВМ = а - r АК = АМ = b - r AB = AM + BM c = b – r + a - r 2r = a + b - c АС, ВС, АВ – касательные и r r b - r а - r b - r а - r a, b- катеты, с - гипотенуза a b c
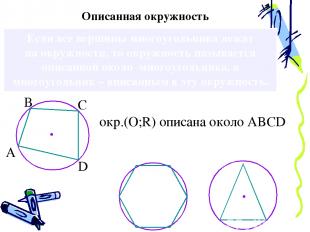
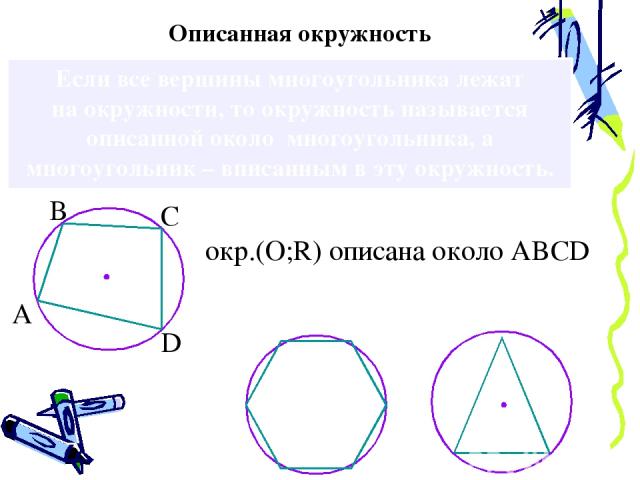
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Описанная окружность окр.(О;R) oписана около ABCD А В С D
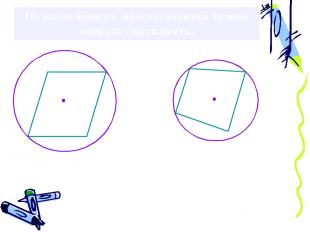
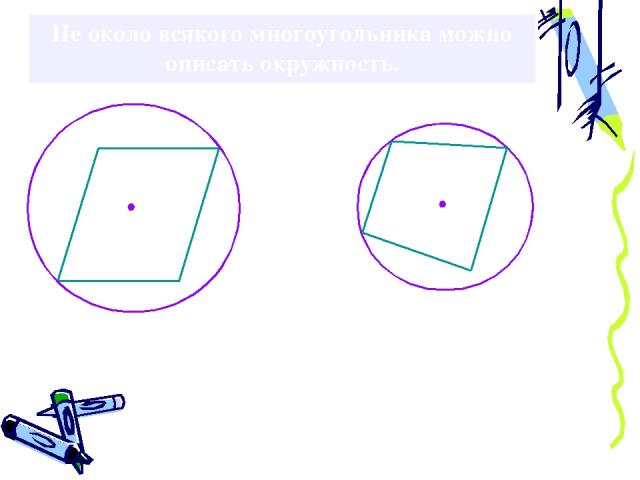
Не около всякого многоугольника можно описать окружность.
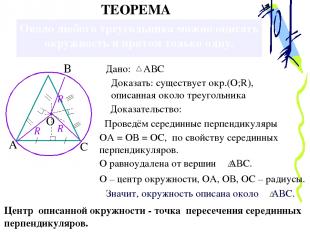
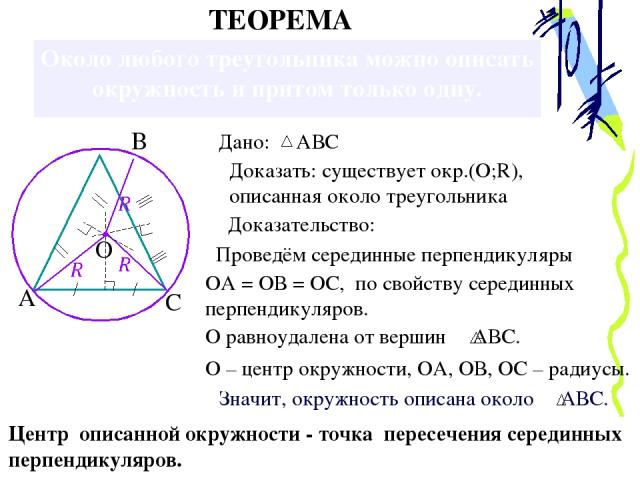
Около любого треугольника можно описать окружность и притом только одну. Доказать: существует окр.(О;R), описанная около треугольника Доказательство: Проведём серединные перпендикуляры ОА = ОВ = ОС, по свойству серединных перпендикуляров. О – центр окружности, ОА, ОВ, ОС – радиусы. ТЕОРЕМА А В С О Центр описанной окружности - точка пересечения серединных перпендикуляров. Дано: АВС Значит, окружность описана около АВС. О равноудалена от вершин АВС.
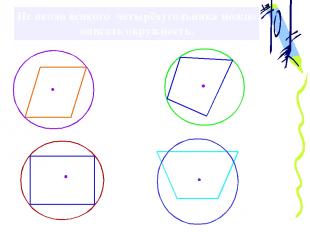
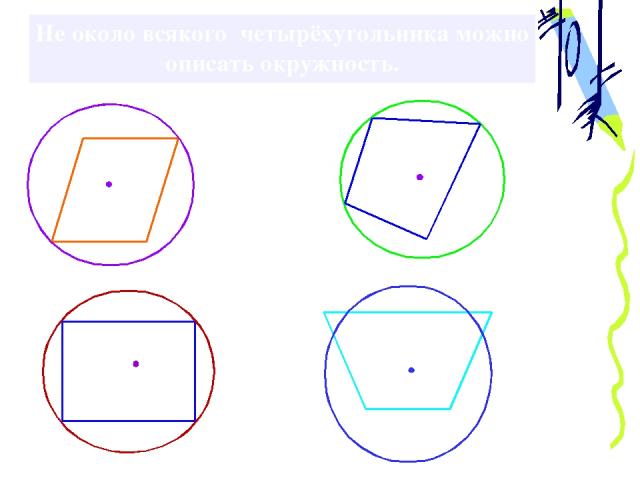
Не около всякого четырёхугольника можно описать окружность.

ТЕОРЕМА Дано: окр.(О;R) описанна около четырехугольник ABCD Доказательство: Доказательство обратной теоремы см. № 729 в учебнике. А В С D