Презентация на тему: Об аксиомах геометрии

Об аксиомах геометрии

Некоторые утверждения о свойствах геометрических фигур принимаются в качестве исходных положений, на основе которых доказываются далее теоремы и, вообще, строится вся геометрия.Такие исходные положения называются аксиомами.

Через любые две точки проходит прямая, и притом только одна.На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

«аксиома» «аксиос» - ценный, достойный

АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ (1792-1856)

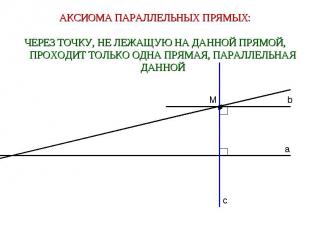
АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ НА ДАННОЙ ПРЯМОЙ, ПРОХОДИТ ТОЛЬКО ОДНА ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ДАННОЙ

УТВЕРЖДЕНИЯ, КОТОРЫЕ ВЫВОДЯТСЯ НЕПОСРЕДСТВЕННО ИЗ АКСИОМ ИЛИ ТЕОРЕМ НАЗЫВАЮТСЯ СЛЕДСТВИЯМИ

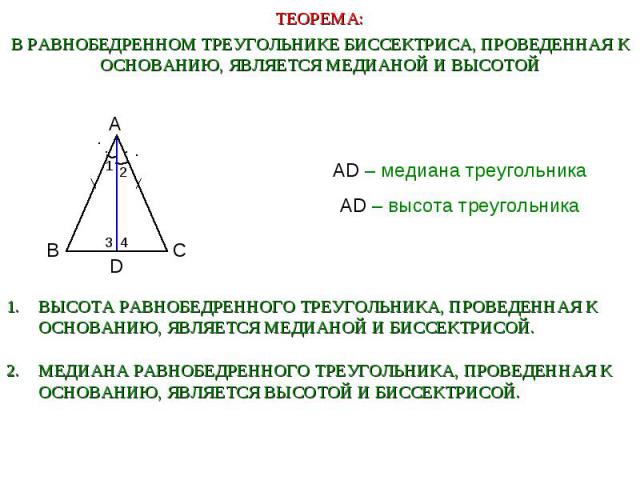
В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕ БИССЕКТРИСА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ, ЯВЛЯЕТСЯ МЕДИАНОЙ И ВЫСОТОЙ AD – медиана треугольника AD – высота треугольника Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

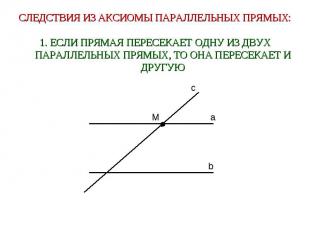
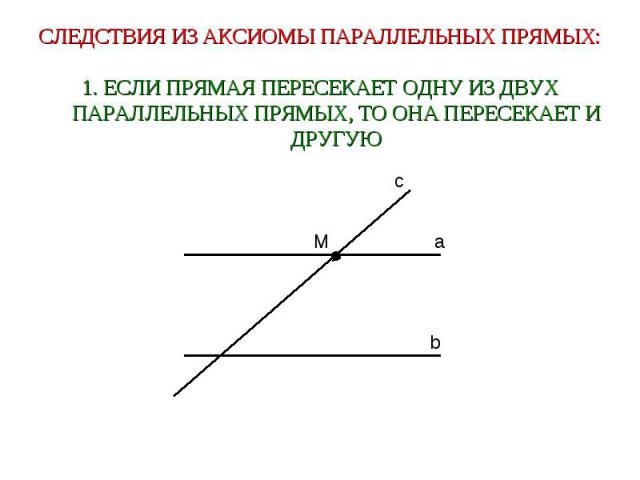
СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:1. ЕСЛИ ПРЯМАЯ ПЕРЕСЕКАЕТ ОДНУ ИЗ ДВУХ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ, ТО ОНА ПЕРЕСЕКАЕТ И ДРУГУЮ

СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ:2. ЕСЛИ ДВЕ ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ ТРЕТЬЕЙ ПРЯМОЙ, ТО ОНИ ПАРАЛЛЕЛЬНЫ