Презентация на тему: Круги Эйлера и их практическое применение

Круги Эйлера и их практическое применение

Выполнила: Жубанова Диана ученица 7 классаКарасаевской СОШ

Цель исследования:Изучить круги ЭйлераНаучиться применять данный способ для решения задач Cоставлять задачи практического содержания.Задачи исследования:Познакомиться с кругами Эйлера, кругами (диаграммами) Эйлера – Венна.Составлять и решать задачи с меняющимися данными условиями.Проанализировать, как изменяется решение задачи при изменении части условия.

Немного об истории Леонард ЭйлерЛеонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Немного об истории Джон Венн Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

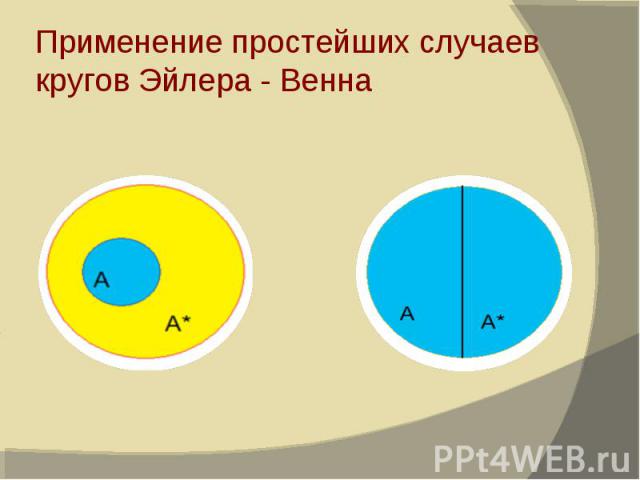
Применение простейших случаев кругов Эйлера - Венна
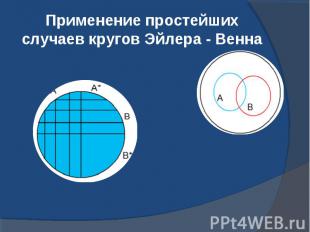
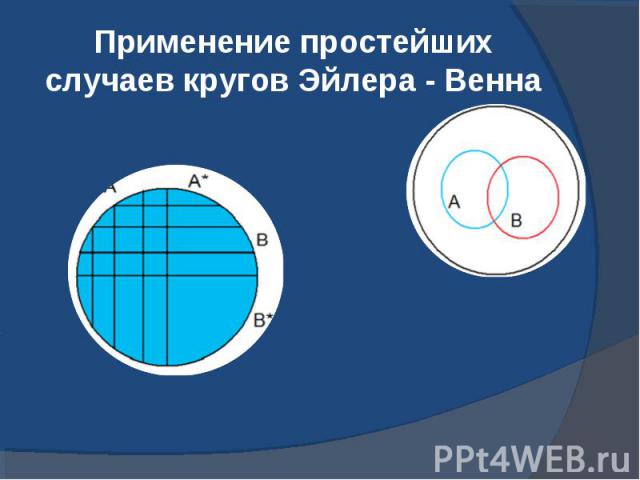
Применение простейших случаев кругов Эйлера - Венна
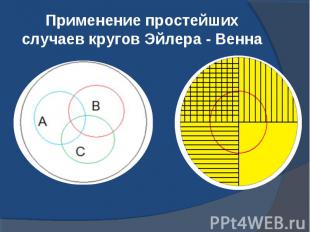
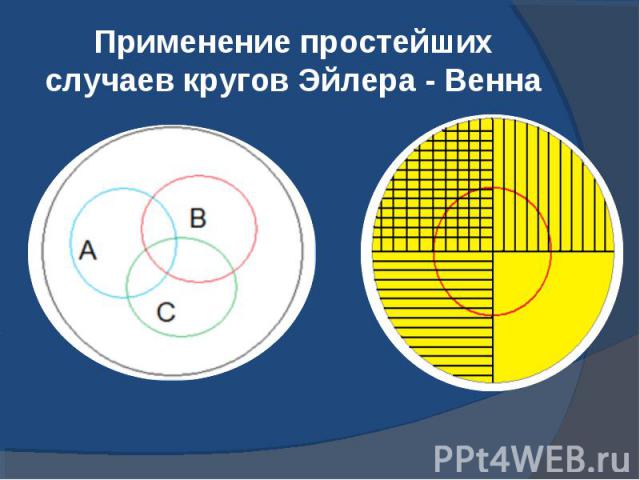
Применение простейших случаев кругов Эйлера - Венна

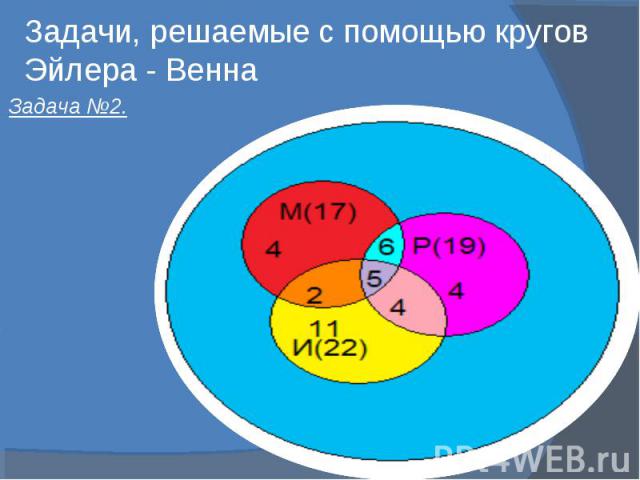
Задачи, решаемые с помощью кругов Эйлера - Венна
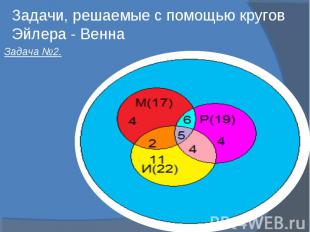
Задачи, решаемые с помощью кругов Эйлера - Венна
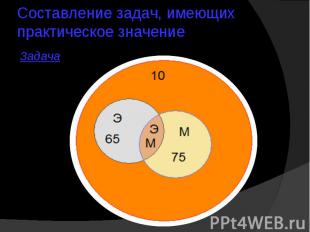
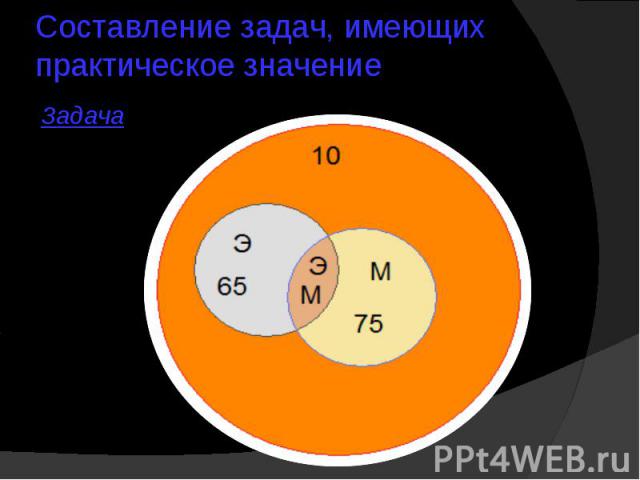
Составление задач, имеющих практическое значение

Составление задач, имеющих практическое значение 1)32-4=28(ч.) – играют хотя бы в одну игру.2)14-6-4-Х=4-Х (ч.) – играют только в баскетбол.3)24-6-4-Х=14-Х (ч.) – играют только в пионербол.4)16-4-4-Х=8-Х (ч.) – играют только в волейбол.5)4-Х+14-Х+8-Х+4+6+4=29 (ч.)40-3Х=283Х=12Х=4(ч.)
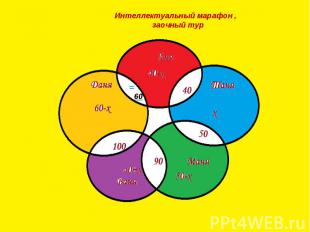
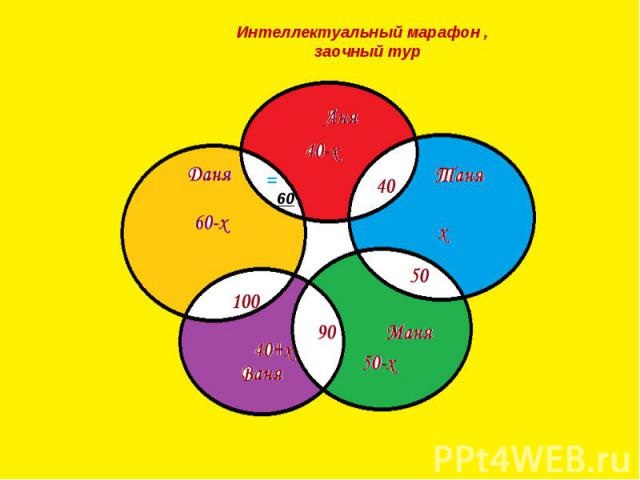
Интеллектуальный марафон , заочный тур

Заключение Ты человек, а значит, тыОбязан рассуждать –А без логичной простотыТы будешь пропадать.Пусть за собой она зовёт –Уйми в коленях дрожь!Коль с Логикой пойдёшь вперёд –Нигде не пропадёшь!(С. Алдошин)

Заключение Алгоритм решения задач с помощью кругов Эйлера - ВеннаЗаписываем краткое условие задачи.Выполняем рисунок.Записываем данные в круги (или в диаграмму Эйлера).Выбираем условие, которое содержит больше свойств.Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).Записываем ответ.

Спасибо за внимание!!!