Презентация на тему: Касательная к окружности

Касательная к окружности Учитель математики ГБОУ Гимназии №1592 Крайнюк А.Л.

Математический диктант Iвариант IIвариант 1. Напишите определение синуса 1. Напишите определение косинуса 2. Основное тригонометрическое тождество 2. Как найти тангенс острого углапрямоуголь-ноготреугольника? 3. Что называется диаметром окружности? 3. Что называется хордой? 4. Что называется окружностью? 4. Что называется радиусом окружности? 5. Запишитеопределение касательной к окружности 5. Запишите определение секущей к окружности 6. В каком случае прямая и окружность имеют двеобщие точки? 6. В каком случае прямая и окружность имеют однуобщую точку?

Определение: прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка – точкой касания прямой и окружности.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания p А О
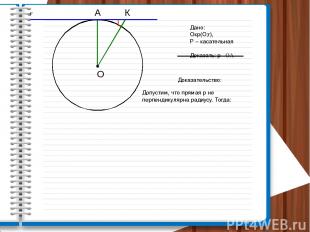
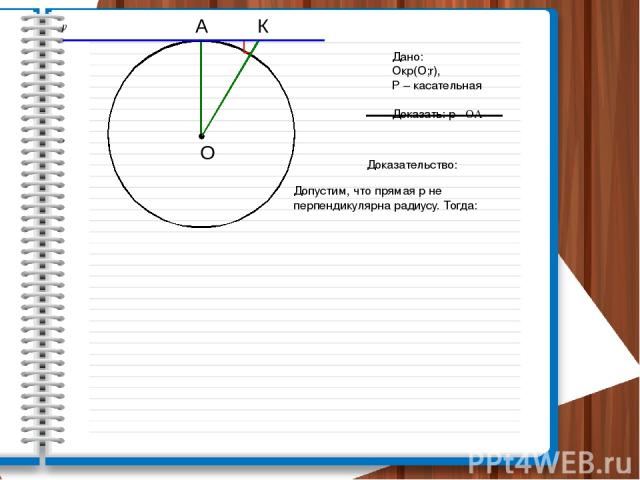
p А Дано: Окр(О;r), Р – касательная Доказать: р┴ ОА Доказательство: Допустим, что прямая р не перпендикулярна радиусу. Тогда: К О
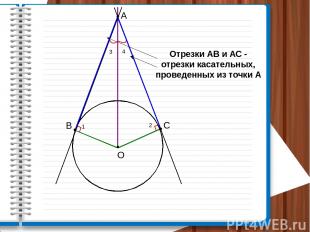
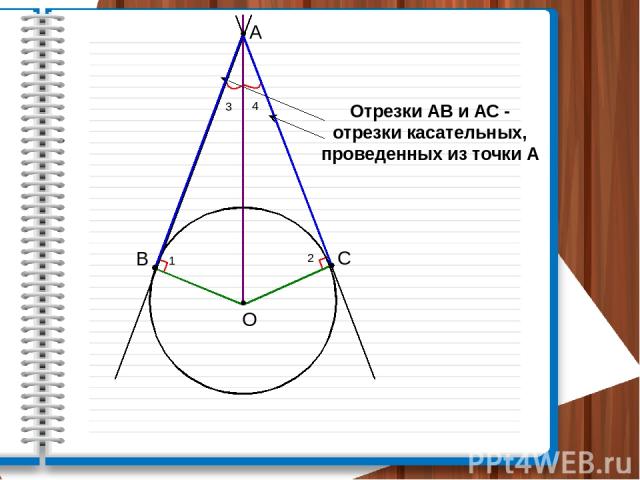
А B C Отрезки АВ и АС - отрезки касательных, проведенных из точки А 1 2 3 4 О

Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности Дано: Окр(О;r) АВ, АС – касательные АВ∩АС = А

p А Дано: Окр(О;ОА), ОА┴р Доказать: р – касательная ЕСЛИ ПРЯМАЯ ПРОХОДИТ ЧЕРЕЗ КОНЕЦ РАДИУСА, ЛЕЖАЩЕГО НА ОКРУЖНОСТИ, И ПЕРПЕНДИКУЛЯРНА К ЭТОМУ РАДИУСУ, ТО ОНА ЯВЛЯЕТСЯ КАСАТЕЛЬНОЙ О
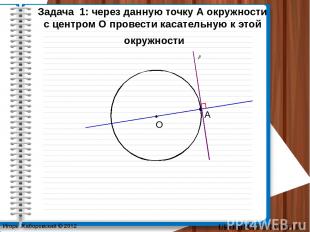
UROKIMATEMATIKI.RU Игорь Жаборовский © 2012 А Задача 1: через данную точку А окружности с центром О провести касательную к этой окружности p О

Задача 2: Дан прямоугольник АВСD, где АВ = 8см, а ВС = 6 см. Какие из прямых АС, ВС, CD и BD являются секущими по отношению к окружности с центром в т. А радиуса 6 см. А В С D

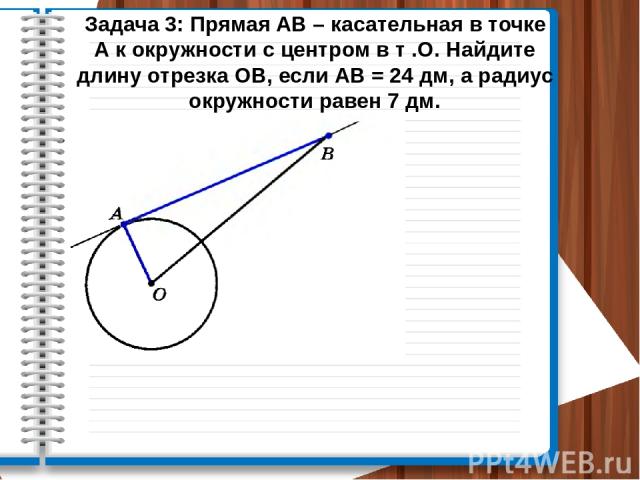
Задача 3: Прямая АВ – касательная в точке А к окружности с центром в т .О. Найдите длину отрезка ОВ, если АВ = 24 дм, а радиус окружности равен 7 дм.
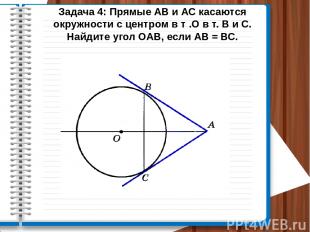
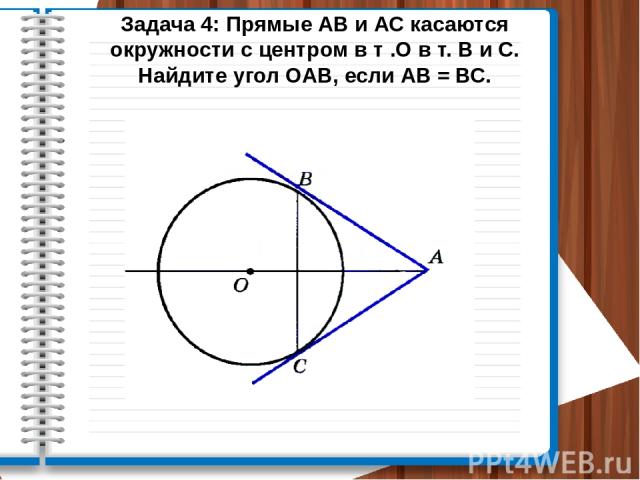
Задача 4: Прямые АВ и АС касаются окружности с центром в т .О в т. В и С. Найдите угол ОАВ, если АВ = ВС.

Домашнее задание: П.69 №634, №636, №639