Презентация на тему: Термодинамические процессы изменения состояния идеального газа

Тема №4. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИЗМЕНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА 4.1. ОБЩИЕ ВОПРОСЫ ИССЛЕДОВАНИЯ ПРОЦЕССОВ Большое значение для теоретических исследований и для прикладных работ имеют следующие процессы: изохорный, протекающий при постоянном объеме, изобарный – при постоянном давлении, изотермический – при постоянной температуре, адиабатный – без теплообмена с окружающей средой. Кроме того, существуют еще политропные процессы, которые при определенных условиях могут переходить во все вышеперечисленные процессы. Для всех процессов устанавливается следующий общий метод исследования. 1. Выводится уравнение кривой процесса в pv и Ts координатах. 2. Устанавливается соотношение между основными параметрами состояния рабочего тела в начале и в конце процесса. 3. Определяется изменение внутренней энергии по формуле (4.1) или при постоянной теплоемкости (4.2)

4. Определяется работа изменения объема газа .(4.3) 5. Находится удельное количество теплоты, участвующее в процессе . 6. Находится изменение удельной энтропии по формулам ассматриваемые процессы считаются обратимыми.

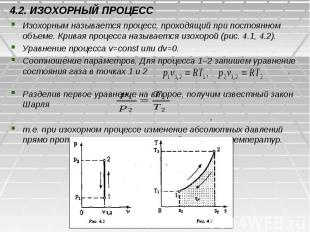
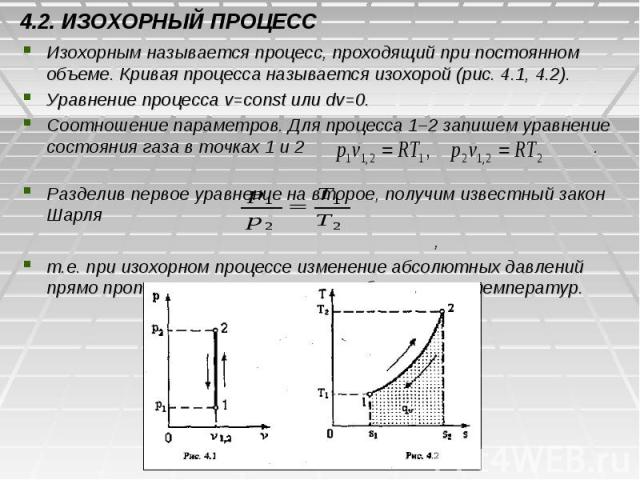
4.2. ИЗОХОРНЫЙ ПРОЦЕСС Изохорным называется процесс, проходящий при постоянном объеме. Кривая процесса называется изохорой (рис. 4.1, 4.2). Уравнение процесса v=const или dv=0. Соотношение параметров. Для процесса 1–2 запишем уравнение состояния газа в точках 1 и 2 . Разделив первое уравнение на второе, получим известный закон Шарля , т.е. при изохорном процессе изменение абсолютных давлений прямо пропорционально изменению абсолютных температур.

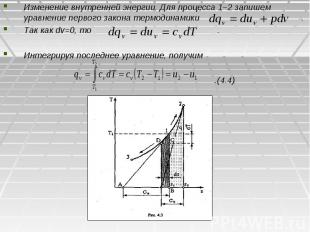
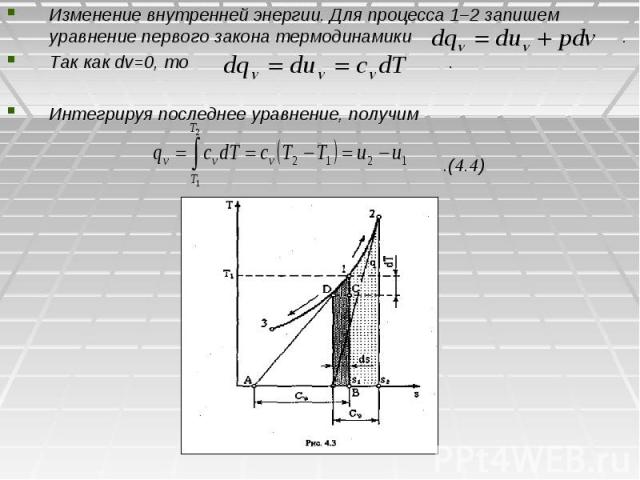
Изменение внутренней энергии. Для процесса 1–2 запишем уравнение первого закона термодинамики . Так как dv=0, то . Интегрируя последнее уравнение, получим .(4.4)

Работа изменения объема газа. Ввиду того, что dv=0, работа dl=pdv=0. То есть работа в изохорном процессе равна нулю, и вся теплота, подводимая (отводимая) к рабочему телу, идет на изменение внутренней энергии. Удельная располагаемая работа l0 определяется по формуле . Удельное количество теплоты определяется по формуле (4.4). 6. Изменение удельной энтропии найдем из уравнений первого и второго законов термодинамики. Запишем уравнение первого начала в виде . Разделив обе части этого уравнения на Т, получим .(4.5) Из уравнения состояния идеального газа следует, что .(4.6) Подставляя (4.6) в (4.5), найдем

Так как , то . Интегрируя последнее соотношение, будем иметь .(4.7) Так как в изохорном процессе , то . Тогда Изображение термодинамического процесса в Ts координатах имеет ряд удобств. Как уже указывалось выше, площадью под кривой процесса определяется количество теплоты. Кроме того, используя кривую изохорного процесса в Ts координатах, можно определить значение истинной теплоемкости сv .

4.3. ИЗОБАРНЫЙ ПРОЦЕСС Изобарными называются процессы, протекающие при постоянном давлении. Кривые процессов называются изобарами (рис. 4.4, 4.5). 1. Уравнение процесса p=const или dp=0. 2. Соотношение параметров. Для процесса 1–2 запишем уравнение состояния в точках 1 и 2 Разделив первое уравнение на второе, получим известный закон Гей-Люссака . 3. Изменение внутренней энергии. Уравнение первого закона термодинамики для изобарного процесса имеет вид .(4.8)

Таким образом, в изобарном процессе часть теплоты, подведенной к рабочему телу, расходуется на изменение внутренней энергии, а оставшаяся часть идет на совершение внешней работы. Для определения долей теплоты, затрачиваемой на изменение внутренней энергии и на совершение работы, разделим уравнение (4.8) на dqp. Отсюда . Если принять k=1,4, что соответствует двухатомным газам, то . Следовательно, 28,5% всей подведенной к рабочему телу теплоты в изобарном процессе для двухатомного газа расходуется на совершение внешней работы, а 71,5% – на изменение внутренней энергии. Запишем уравнение первого закона термодинамики через энтальпию Так как dp=0, то .(4.9)

Или при cp=const. Следовательно, в изобарном процессе теплота, подведенная к рабочему телу, идет на увеличение энтальпии. Количество теплоты, подведенное к рабочему телу в изобарном процессе, измеряется площадью под кривой процесса (рис. 4.5). 4. Работа в изобарном процессе будет dl = pdv, или Располагаемая работа , т.к. dp=0. 5. Удельное количество теплоты определяется по уравнениям (4.8), (4.9). 6. Изменение удельной энтропии найдем из формулы (4.7), используя соотношение параметров изобарного процесса Так как по уравнению Майера , то

Из уравнения Майера следует, что ср > cv. Поэтому изменение энтропии при изобарном процессе будет больше, чем при изохорном . Из сопоставления рис. (4.3) и (4.6) следует, что изобара 1–2 (рис. 4.5) при одинаковых температурах Т1 и Т2, более пологая кривая, чем изохора 1 – 2'.

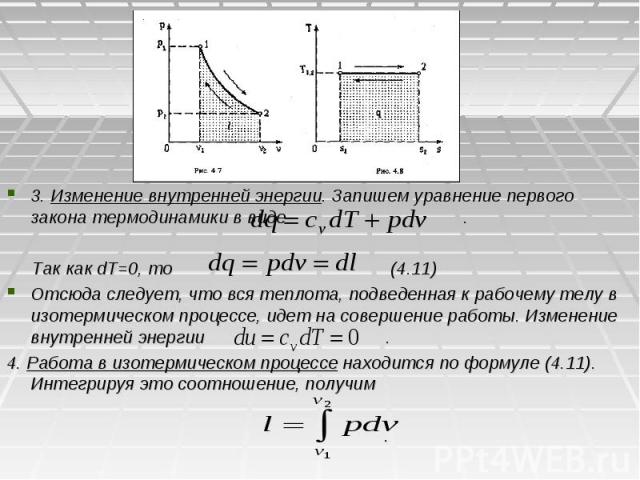
4.4. ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС Изотермическим называется процесс, протекающий при постоянной температуре. Кривая процесса называется изотермой (рис. 4.5, 4.6). 1. Уравнение процесса T=const или dT=0. 2. Соотношение параметров. Уравнение состояния идеального газа в точках 1 и 2 изотермического процесса будет Поделив первое уравнение на второе, получим ,или .(4.10) Отсюда получаем еще одно уравнение изотермического процесса . Из соотношения (4.10) следует, что объем газа изменяется обратно пропорционально его давлению (закон Бойля – Мариотта).

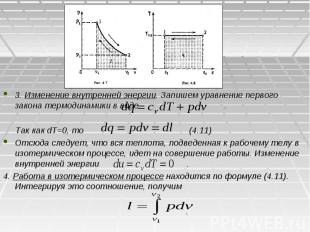
3. Изменение внутренней энергии. Запишем уравнение первого закона термодинамики в виде . Так как dT=0, то (4.11) Отсюда следует, что вся теплота, подведенная к рабочему телу в изотермическом процессе, идет на совершение работы. Изменение внутренней энергии . 4. Работа в изотермическом процессе находится по формуле (4.11). Интегрируя это соотношение, получим .

Так как из уравнения состояния идеального газа , то или Удельная располагаемая работа находится по формуле Таким образом, в изотермическом процессе идеального газа работа изменения объема l, располагаемая работа l0 и удельное количество теплоты равны между собой . Теплоемкость в изотермическом процессе , так как dT=0. Отсюда следует, что теплоемкость в изотермическом процессе не может быть определена.

5. Удельное количество теплоты, участвующее в изотермическом процессе, будет dq=Tds. Интегрируя, получим . 6. Изменение удельной энтропии в изотермическом процессе определяется отношением . Отсюда , . Интегрируя, получим

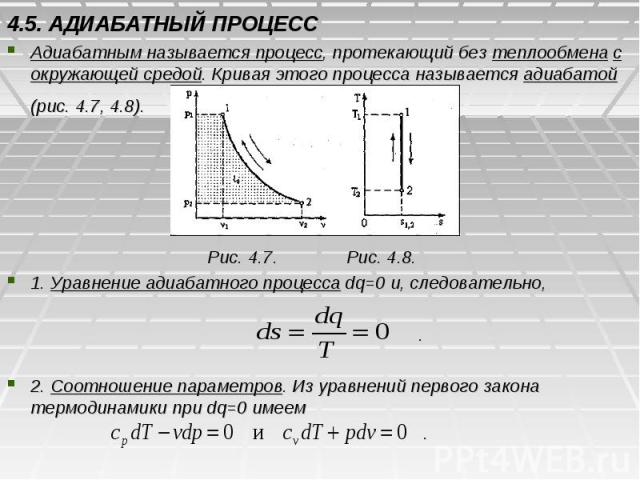
4.5. АДИАБАТНЫЙ ПРОЦЕСС Адиабатным называется процесс, протекающий без теплообмена с окружающей средой. Кривая этого процесса называется адиабатой (рис. 4.7, 4.8). Рис. 4.7. Рис. 4.8. 1. Уравнение адиабатного процесса dq=0 и, следовательно, . 2. Соотношение параметров. Из уравнений первого закона термодинамики при dq=0 имеем .

Разделив первое уравнение на второе, получим , или .(4.12) Интегрируя последнее уравнение при k=const, cp =const и cv =const, будем иметь . Отсюда . Последнее соотношение является еще одним уравнением адиабатного процесса. 3. Изменение внутренней энергии и работа в адиабатном процессе определяются из уравнения первого закона термодинамики при dq=0 . Интегрируя, получим . Таким образом, в адиабатном процессе работа совершается за счет убыли внутренней энергии. Работа в адиабатном процессе может также определяться по следующей формуле , где .

Так как из уравнения состояния , то формула для работы примет вид . Вынося за скобки, получим Учитывая, что и , получим ; Располагаемая работа находится по формуле . При обратимом адиабатном процессе располагаемая работа будет в k раз больше удельной работы расширения газа и противоположна ей по знаку. Для доказательства преобразуем соотношение (4.12) к виду . Отсюда или (4.12а)

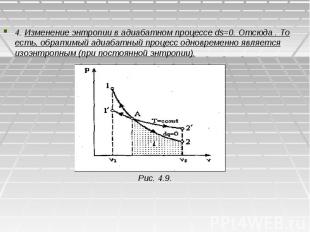
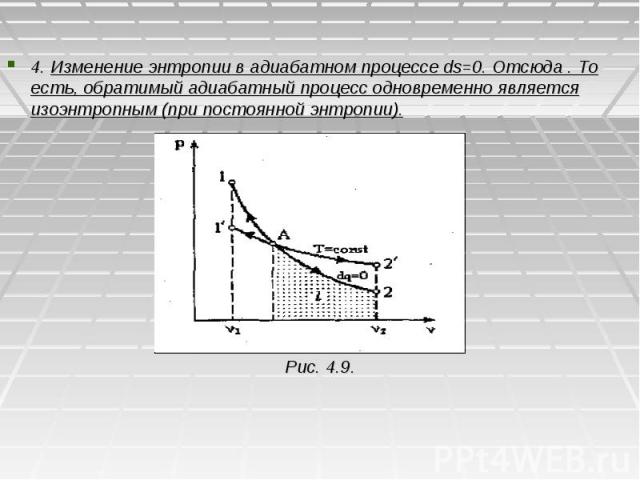
4. Изменение энтропии в адиабатном процессе ds=0. Отсюда . То есть, обратимый адиабатный процесс одновременно является изоэнтропным (при постоянной энтропии). Рис. 4.9.

4.6. ПОЛИТРОПНЫЙ ПРОЦЕСС Политропным называется процесс, в котором удельная теплоемкость остается постоянной величиной, а линию процесса называют политропой. Политропы – это кривые, описывающие газовые процессы, в которых происходит изменение всех термодинамических параметров. 1. Уравнение политропного процесса. Удельное количество теплоты, участвующее в политропном процессе, определяется по формуле ,(4.13) где с – теплоемкость политропного процесса. Подставляя (4.13) в уравнения первого закона термодинамики (2.2) и (2.7), получим Разделим второе уравнение на первое . Обозначая , получим .

После интегрирования найдем .(4.14) Полученное уравнение является уравнением политропного процесса, где п показатель политропы. Показатель политропы п изменяется в пределах от -∞ до +∞. В частных случаях, когда п принимает определенные значения, политропный процесс может переходить в любой из рассмотренных выше процессов. Например–при п=±∞ из уравнения (4.14), записанного в виде , следует, что v=const, т.е. получаем изохорный процесс. При n=0 согласно (4.14) получим изобарный процесс; п=1 – изотермический и при n=k – адиабатный. Таким образом, политропный процесс является обобщающим для всех рассмотренных выше процессов. 2. Соотношение параметров. Так как уравнение политропы аналогично уравнению адиабаты, то, заменив показатель адиабаты показателем политропы, можно записать следующие уравнения, связывающие основные термодинамические параметры

3. Работа в политропном процессе. По аналогии с выражениями для работы в адиабатном процессе, заменяя k на n, получим следующие выражения для определения работы в политропном процессе Аналогично, располагаемая работа будет .(4.14а) Таким образом, располагаемая работа в политропном процессе в п раз больше работы расширения. Теплоемкость в политропном процессе определяется по формуле .(4.15)

4. Изменение энтропии в политропном процессе определяется по формулам Подставляя значение теплоемкости из (4.15) в соотношение , получим . После интегрирования находим . Учитывая уравнение (4.14) и соотношение , получим , или .