Презентация на тему: Создание и использование тренажеров

6 л можно получить только в семилитровом сосуде, для этого достаточно получить 4 л в пятилитровом сосуде и из семилитрового отлить 1 л или получить в семилитровом сосуде 1 л и долить туда 5 л. 6 л можно получить только в семилитровом сосуде, для этого достаточно получить 4 л в пятилитровом сосуде и из семилитрового отлить 1 л или получить в семилитровом сосуде 1 л и долить туда 5 л. Оба варианта приведены в таблицах:

Сначала пронумеруем пакеты. Потом взвесим пакеты 1 и 2, 2 и 3, 1 и 3. Сначала пронумеруем пакеты. Потом взвесим пакеты 1 и 2, 2 и 3, 1 и 3. В результате эти три пакета за три взвешивания расположим по весу. Теперь взвесим четвертый и средний по весу пакет. Наконец, взвесим четвертый и самый легкий (или самый тяжелый) пакет.

Разобьем конфеты на кучки: Разобьем конфеты на кучки: ☼ ☼ ☼ ☼ ☼ ☼ ☼ ☼ ☼ ☼ ☼ Для выигрыша начинающему надо взять сначала 2 конфеты, а затем такое число, которое вместе с числом конфет, взятых соперником, дает в сумме 4.

До первой встречи пешеходы прошли пути, сумма которых равна АВ = S. До первой встречи пешеходы прошли пути, сумма которых равна АВ = S. В промежутке же между первой и второй встречей – пути, сумма которых равна 2S. Поэтому промежуток времени между первой и второй встречами будет также в 2 раза больше промежутка времени до первой встречи. Следовательно, путь, пройденный пешеходом из А между встречами, равен (S – 300 + 400) м и в 2 раза больше пути, пройденного им до первой встречи (300м) а значит, имеем уравнение S – 300 + 400 = 2 * 300

1. Если все числа первого набора взяты с плюсами, а второго с минусами, то сумма максимальна и равна 1. Если все числа первого набора взяты с плюсами, а второго с минусами, то сумма максимальна и равна 9∙(4+5+6+7+8)-5∙(-11-12-13-14-15-16-17-18-19)=

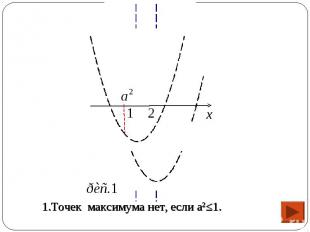
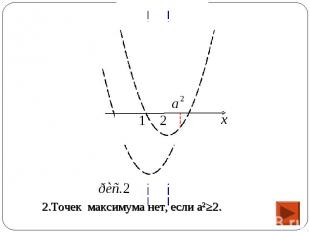
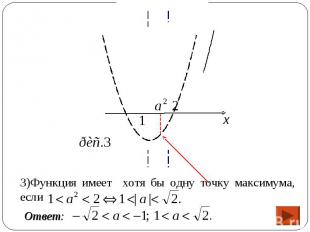
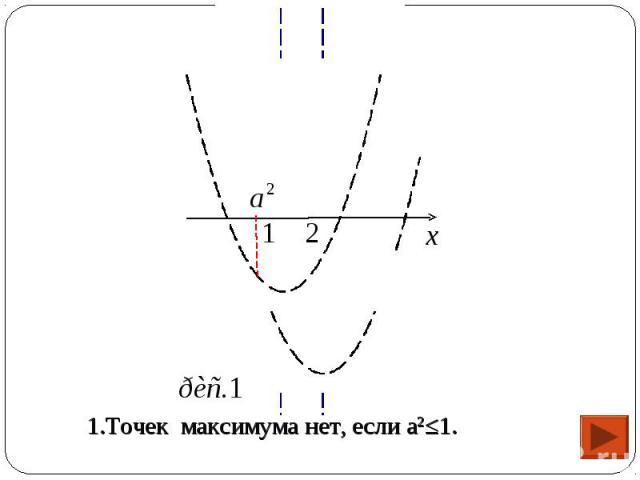
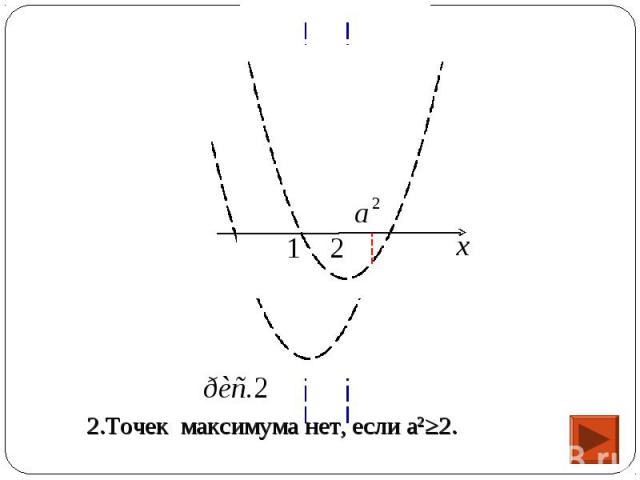
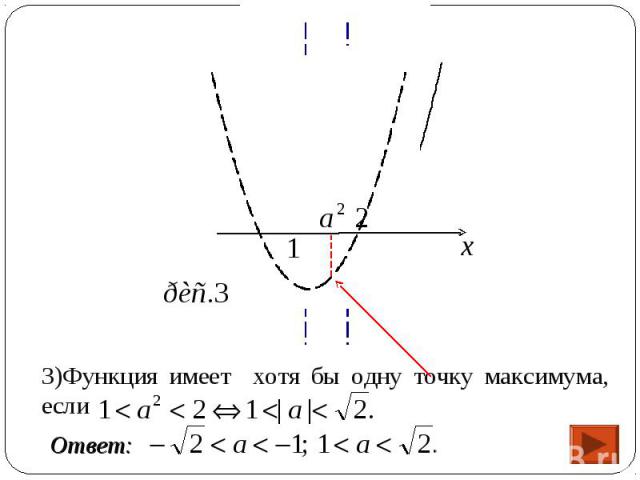
1) Функция f имеет вид: 1) Функция f имеет вид: а) при х≥а2 : f(x)=(x-2)2+а2-4, поэтому ее график есть часть параболы с ветвями вверх, и осью симметрии х=2.