Презентация на тему: Основы теории проверки статистических гипотез

Доцент Аймаханова А.Ш.

1. Статистические гипотезы в медико- биологических исследованиях. 2. Параметрические критерии различий. 3. Непараметрические критерии. 4. Критерии согласия.

Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез. Задачи статистической проверки гипотез: Относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н0. Из этой генеральной совокупности извлекается выборка. Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н0 или принять ее.

Статистическая гипотеза- это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может быть проверена на основании выборочных показателей. Примеры статистических гипотез: Генеральная совокупность распределена по нормальному закону Гаусса. Дисперсии двух нормальных совокупностей равны между собой.

Параметрические Непараметрические

Нулевой гипотезой Н0 называется основная гипотеза, которая проверяется. Альтернативной гипотезой Н1, называется гипотеза, конкурирующая с нулевой, то есть противоречащая ей. Простой называют гипотезу, содержащую только одно предположение. a=a0 Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Статистическим критерием проверки гипотезы Н0 называется правило, по которому принимается решение принять или отклонить гипотезу Н0.

Проверку гипотез осуществляют на основании результатов выборки X1,X2,…,Xn , из которых формируют функцию выборки Tn=T(X1,X2,…,Xn ), называемой статистикой критерия. Tn=T(X1,X2,…,Xn ) критическая область S область принятия гипотезы

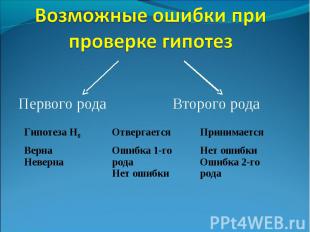
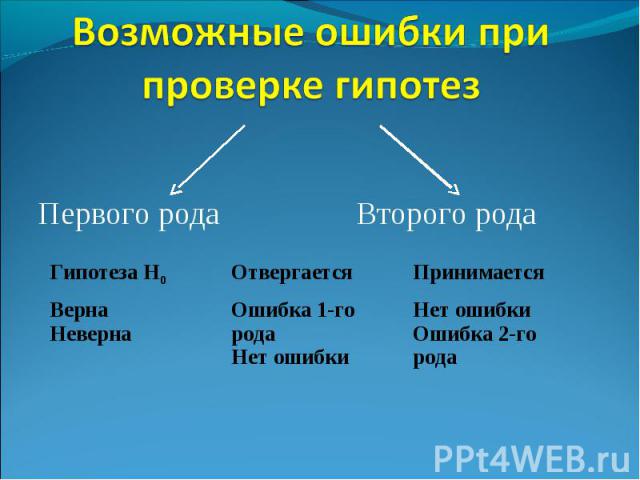
Первого рода Второго рода Гипотеза Н0 Отвергается Принимается Верна Неверна Ошибка 1-го рода Нет ошибки Нет ошибки Ошибка 2-го рода

Уровнем значимости критерия () называется вероятность допустить ошибку 1-го рода. Вероятность ошибки 2-го рода обозначается через β. Мощностью критерия называется вероятность недопущения ошибки 2-го рода (1- β). Р(отвергнуть Н0/Н0 верна) или Р(Н1/Н0) βР(принять Н0/Н0 неверна) или βР(Н0 /Н1) 1-βР(принять Н1/Н1 верна) Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше. Разумное соотношение между и β находят, исходя из тяжести последствий каждой из ошибок.

1. Формирование нулевой Н0 и альтернативной Н1 гипотез исходя из выборки X1,X2,…,Xn . 2. Подбор статистики критерия Tn=T(X1,X2,…,Xn ) 3. По статистике критерия Tn и уровню значимости определяют критическую точку tкр, то есть границу, отделяющую область от S. 4. Для полученной реализации выборки Х=(X1,X2,…,Xn ) подсчитывают значение критерия, то есть Tнабл=T(X1,X2,…,Xn )t 5. Если tS (например, t> tкр для правосторонней области S), то нулевую гипотезу Н0 отвергают; если же t (t

Общий вид:

df= n1+n2-2 n1=n2=ndf=n-1 n1≠n2

df=n-1

Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп. Критерий Стьюдента применяется в случае малых выборок, что характерно для медико- биологических экспериментов. Если схема эксперимента предполагает большее число групп, воспользуйтесь дисперсионным анализом. Если критерий Стьюдента был использован для проверки различий между несколькими группами, то истинный уровень значимости можно получить, умножив уровень значимости, на число возможных сравнений.

1>2 df1=n1-1, df2=n2-1

Критерии различия называют непараметрическими, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности. Применение непараметрических методов целесообразно: на этапе разведочного анализа; при малом числе наблюдений (до 30); когда нет уверенности в соответствии данных закону нормального распределения.

Непараметрические критерии представлены основными группами: критерии различия между группами независимых выборок; критерии различия между группами зависимых выборок.

U критерий Манна-Уитни двухвыборочный критерий Колмогорова – Смирнова.

z – критерий знаков Т – критерий Уилкоксона парных сравнений

Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Пирсона (Хи-квадрат), Колмогорова, Фишера, Смирнова.

Н0: «между эмперическим распределением и теоретической моделью нет никакого различия». Если эмпирические частоты (ni) сильно отличаются от теоретических (npi) ,то проверяемую гипотезу Но следует отвергнуть; в противном случае-принять. …… ……

n-объем выборки k-число интервалов разбиения выборки ni-число значений выборки, попавших в і-й интервал npi - теоретическая частота попадания значений случайной величины Х в і-й интервал.

или О-фактически наблюдаемое число Е- теоретически ожидаемое число

Для распределения признаков, которые принимают всего 2 значения.

*По формуле вычисляют - выборочное значение статистики критерия. *выбрав уровень значимости α критерия, по таблице -распределения находим критическую точку *Если ≤ , то гипотеза Н0 не противоречит опытным данным; если > , то гипотеза Н0 отвергается. Неоходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений

Медик В.А.,Токмачев М.С.,Фишман Б.Б.Статистика в медицине и биологии. М.: Медицина, 2000. Лукьянова Е.А. Медицинская статистика.- М.: Изд. РУДН, 2002. Рокицкий П.Ф. Биологическая статистика.- Высшая школа, 1973. И.В. Павлушков и др. Основы высшей математики и математической статистики. (учебник для медицинских и фармацевтических вузов) М., «ГЭОТАР - МЕД»; 2003

СПАСИБО ЗА ВНИМАНИЕ.