Презентация на тему: Концепция современного естествознания

Неклассическое естествознание Термодинамика и статистическая физика

Закон теплопроводности (1811 г) Французский математик и физик барон Жан-Батист Жозеф Фурье : поток тепла пропорционален градиенту температуры: Q – количество тепла, проходящего через некоторую поверхность S в единицу времени (количество энергии, передаваемой путем теплопередачи); dT/dx – быстрота изменения температуры вдоль оси ОХ (величина градиента температуры), σ – коэффициент теплопроводности. Знак “–“ перед правой частью указывает на то, что тепло распространяется в сторону уменьшения температуры (необратимый процесс установления равновесия).

Термодинамический метод Макроскопический объект рассматривается как сплошная среда, не имеющая внутренней структуры. Состояние макросистемы характеризуется некоторым количеством величин – параметров. Эти величины характеризуют всю систему в целом, в разных точках среды могут иметь различные значения и изменяться с течением времени (неравновесное состояние). Равновесным называется такое состояние, при котором в изолированной системе при отсутствии внешних воздействий все параметры системы приобретают постоянные значения. В термодинамике вместо классического движения рассматривается переход из одного равновесного состояния в другое равновесное состояние.

Термодинамика Промышленная революция первой трети 19 века в Западной Европе потребовала изучения закономерностей превращения теплоты в механическую работу в тепловых двигателях. Пионерские исследования, заложившие основы термодинамики: французский инженер и физик Сади Карно (1796-1832), немецкий физик-теоретик Рудольф Клаузиус (1822-1888) австрийский физик-теоретик Людвиг Больцман (1844-1906). Первые положения термодинамики были изложены в сочинении Сади Карно «О движущей силе огня и о машинах, способных развивать эту силу» (1824 г). Первоначальная задача сводилась к исследованию условий, при которых превращение теплоты в работу является наиболее оптимальным.

Термодинамика Термодинамика – это учение о связи и взаимопревращениях различных видов энергии, теплоты и работы. Первое начало устанавливает количественные соотношения, имеющие место при превращениях энергии из одних видов в другие. Первое начало термодинамики (закон сохранения энергии): количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение работы над внешними телами; невозможен вечный двигатель первого рода, т.е. такой периодически действующий двигатель, который совершал бы работу в большем количестве, чем получал извне энергию.

Термодинамика Второе начало определяет условия, при которых возможны эти превращения, то есть определяет возможные направления процессов. Второе начало термодинамики: невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому; невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.

Молекулярно-кинетическая теория Идеальный газ – это газ, для которого: размерами молекул можно пренебречь; силами межмолекулярного взаимодействия можно пренебречь (на расстоянии молекулы друг с другом не взаимодействуют); друг с другом и со стенками сосуда молекулы взаимодействуют по законам абсолютно упругого удара. Состояние идеального газа описывается уравнением Менделеева-Клайперона

Молекулярно-кинетическая теория Основные положения МКТ – полная хаотичность движения молекул. При столкновениях выполняется закон сохранения энергии движения. Между столкновениями молекулы движутся свободно, т.е. по прямым линиям с постоянной скоростью; – средние кинетические энергии молекул разных газов, находящихся при одинаковой температуре равны между собой. – средняя скорость молекул пропорциональна корню квадратному из абсолютной температуры;

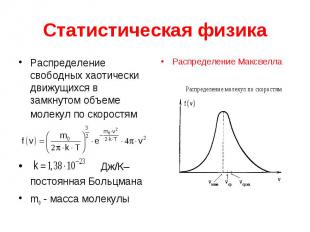
Статистическая физика Распределение свободных хаотически движущихся в замкнутом объеме молекул по скоростям Дж/К– постоянная Больцмана m0 - масса молекулы

Статистическая физика f(v) - вероятность того, что величина скорости каждой отдельной частицы находится в единичном интервале скоростей около скорости . вероятность того, что скорость любой частицы ансамбля принимает какое-либо значение в интервале от нуля до бесконечности, равна единице. Зная f(v), можно вычислить число частиц , модули скоростей которых лежат в интервале значений от v1 до v2.

Статистическая физика Каждая отдельная молекула ансамбля может иметь любое значение скорости, однако при этом конкретному состоянию ансамбля частиц соответствуют вполне определенные значения скоростей и энергии: Средняя скорость Среднеквадратичная скорость Средняя кинетическая энергия

Статистическая физика Макроскопическое состояние сложной системы описывается статистически. В изолированной системе частиц, находящейся в состоянии теплового равновесия, динамическое состояние каждой отдельной молекулы непрерывно изменяется, а макросостояние системы в целом остается стационарным, т.е. характеризуется постоянными значениями температуры и давления. Классическая статистическая механика (Больцман) позволяет предсказывать свойства систем на основе анализа статистического поведения частиц, из которых они состоят.

Статистическая физика Важнейшим понятием статистической физики является вероятность. Под вероятностью понимается предел, к которому стремиться относительная частота появления некоторого события при достаточно большом числе повторений опыта при неизменных внешних условиях.

Статистическая физика Новые идеи Максвелла и Больцмана составили основу последующего развития естествознания (неклассического) – введение вероятности в физике, как объясняющего принципа, а не как аппроксимации; – использование вероятностей и статистического подхода к исследованию микросостояний сложных систем для предсказания макроскопических свойств.

Статистическая физика Понятие энтропии. Всякое макросостояние может быть реализовано различными способами, каждому из которых соответствует некоторое микросостояние. Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом, или термодинамической вероятностью.

Статистическая физика Пример: как 4 молекулы могут распределяться между двумя половинками сосуда; способов 24=16

Статистическая физика В общем случае число микросостояний, отвечающих макросостоянию Вероятность макросостояния равна отношению его статистического веса к полному числу состояний. Отметим, что не обладает свойство аддитивности. Если система, к примеру, состоит из двух подсистем, то = 1 2. Поэтому в качестве характеристики вероятности состояния принимается величина S=k ln , которая называется энтропией.

Статистическая физика Закон возрастания энтропии (второе начало термодинамики): Энтропия изолированной системы возрастает, т.к. система переходит из менее вероятных в более вероятные состояния; Энтропия системы, находящейся в равновесном состоянии, максимальна.

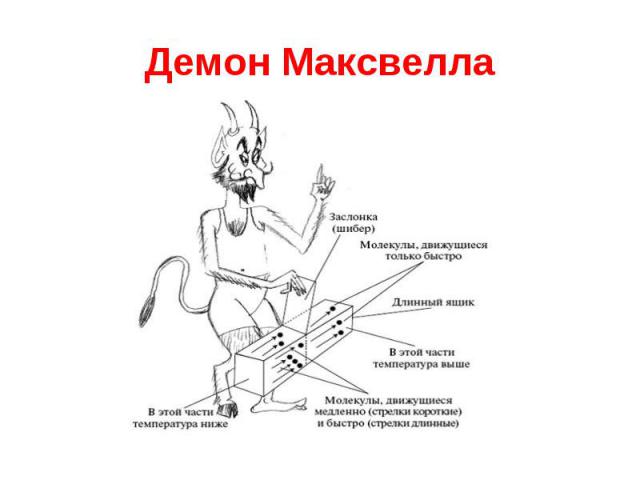
Демон Максвелла "Понедельник начинается в субботу" А. и Б. Стругацких: Демон Максвелла -- важный элемент мысленного эксперимента крупного английского физика Максвелла. Предназначался для нападения на второй принцип термодинамики. В мысленном эксперименте Максвелла демон располагался рядом с отверстием в переборке, разделяющей сосуд, наполненный движущимися молекулами. Работа демона состоит в том, чтобы выпускать из одной половины сосуда в другую быстрые молекулы и закрывать отверстия перед носом медленных. Идеальный демон способен таким образом без затраты труда создать очень высокую температуру в одной половине сосуда и очень низкую -- в другой, осуществляя вечный двигатель второго рода.

Демон Максвелла

Статистическая физика Состояние, осуществляемое относительно малым числом способов, называется упорядоченным. Энтропия является мерой молекулярного беспорядка в системе. Тепловое движение приводит к увеличению степени беспорядка в системе (увеличению энтропии). Сообщение системе тепла приводит к усилению теплового движения и увеличению энтропии.

Статистическая физика При абсолютном нуле температуры всякое тело находится в основном состоянии, статистический вес которого равен единице т.е. Теорема Нернста (третье начало термодинамики) энтропия всякого тела стремится к нулю при стремлении к нулю его температуры.