Презентация на тему: Связь математики и музыки

Математика в музыке 900igr.net

Авторы проекта: Мячина Екатерина, Попова Екатерина, Носова Дарья Представляют: Борисенко Екатерина, Ергашова Анастасия, Видинеева Дарья Руководитель: Акулова Анна Сергеевна Цель проекта: 1) Расширить свои познания о взаимосвязи музыки и математики 2) Найти и узнать новые исследования Пифагора в музыке 3) Рассмотреть применение математики в музыке Гипотеза: «Музыка есть таинственная арифметика души; она вычисляет, сама того не сознавая… » Краткое содержание работы: 1) Открытия Пифагора в музыке 2) Монохорд 3) Логарифмы и музыка 4) Звуковые соотношения 5) Терминология 6) Рациональность и аффект Аннотация к проекту

Открытия Пифагора в музыке Согласно легенде, бог Гермес сконструировал первую лиру, натянув струны на панцирь черепахи. Если древние китайцы, индусы, персы, египтяне, израильтяне и греки использовали вокальную и инструментальную музыку в своих религиозных церемониях как дополнение к поэзии и драме, то Пифагор поднял искусство до истинно достойного состояния, продемонстрировав его математические основания

Хотя сам он не был музыкантом, именно Пифагору приписывают открытие диатонической шкалы. Получив основные сведения о священной теории музыки от жрецов различных мистерий, Пифагор провел несколько лет в размышлениях над законами, управляющими созвучием и диссонансом

Как он в действительности нашел решение, нам не известно, но было следующее объяснение: Однажды, Пифагор проходил мимо мастерской медника, который склонился над наковальней с куском металла. Заметив различие в тонах между звуками, издаваемыми различными молоточками и другими инструментами при ударе о металл, и тщательно оценив гармонии и дисгармонии, Пифагор получил первый ключ к понятию музыкального интервала в диатонической шкале

К первой из них прикрепил вес в двенадцать фунтов, ко второй — в девять, к третьей — в восемь и к четвертой — в шесть фунтов. Эти различные веса соответствовали весу молотков медника Он вошел в мастерскую и после тщательного осмотра инструментов и оценки в уме их веca вернулся в собственный дом, сконструировал балку, и приделал к ней через равные интервалы четыре струны, во всем одинаковые

Пифагор разработал свою теорию гармонии, работая с монохордом, однострунным инструментом

Монохорд Изобретение этого прибора приписывается Пифагору. Он состоит из деревянного ящика, на верхней стороне которого натянуты две струны. Одна из струн служит только для сравнения тонов, и напряженность ее регулируется посредством колка. Вторая же струна только одним своим концом неподвижно прикреплена к монохорду, другой же перекидывается через блок и натягивается гирею

Монохорд

Логарифмы и музыка Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека, и что между ними размещается все, что человечество создало в области науки и искусства Г. Нейгауз.

Звуковые соотношения Естественно, что на протяжении многих веков люди не знали таких слов, как интервал, гамма, музыкальный строй. В таком случае возникает вопрос: кто же стоял у истоков построения мажора и минора, аккордов и интервалов? А у истоков стоял не кто иной, как великий математик Пифагор. Его открытие в области теории музыки послужило базой для развития математических пропорций в музыке

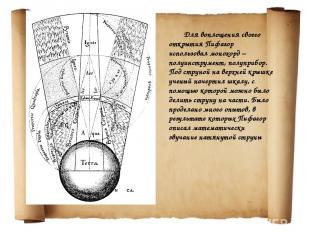
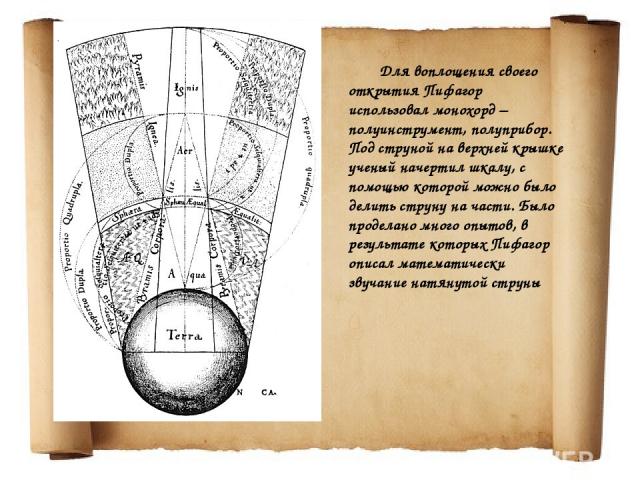
Для воплощения своего открытия Пифагор использовал монохорд – полуинструмент, полуприбор. Под струной на верхней крышке ученый начертил шкалу, с помощью которой можно было делить струну на части. Было проделано много опытов, в результате которых Пифагор описал математически звучание натянутой струны

Основой музыкальной шкалы – гаммы пифагорейцев был интервал октава. Для построения музыкальной гаммы пифагорейцам требовалось разделить октаву на красиво звучащие части. Так как они верили в совершенные пропорции, то связали устройство гаммы со средними величинами: арифметическим, геометрическим, гармоническим

Оказывается, гамму можно построить, пользуясь лишь совершенными консонансами – квинтой и октавой. Суть этого метода состоит в том, что от исходящего звука, например «до» (3/2)0=1, мы движемся по квинтам вверх и вниз и полученные звуки собираем в одну октаву. И тогда получаем: (3/2)1 =3/2 – соль, (3/2)2 /2 =9/8 – ре, (3/2)3 /2 =27/16 – ля, (3/2)4 /4 =81/64 – ми, (3/2)5 /4 =243/128 – си, (3/2)–1 /2 =4/3 – фа.

В гармонии звуков пифагорейцами была воплощена гармония космоса.Идея совершенства окружающего мира владела умами ученых и в последующие эпохи.В первой половине девятнадцатого века И. Кеплер установил 7 основных гармонических интервалов: 2/1 – октаву, 5/3 – большую сексту, 8/5 – малую сексту, 3/2 – чистую квинту, 4/3 – чистую кварту, 5/4 – большую терцию, 6/5 – малую терцию

С помощью этих интервалов он выводит весь звукоряд как мажорного, так и минорного наклонения. После долгих поисков гармоничных отношений на «небе», проделав огромную вычислительную работу, Кеплер установил, что отношения экстремальных углов скоростей для некоторых планет близки к гармоническим: 3/2 – Марс, 6/5 – Юпитер, 5/4 – Сатурн.

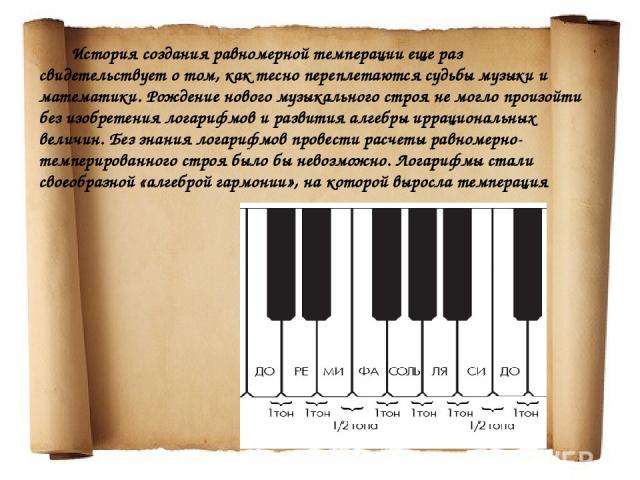
XVIII век открыл новые страницы в истории музыки. Около 1700 года немецкий органист А. Веркмайстер осуществил гениальное решение: отказался от совершенных и несовершенных консонансов пифагорейской гаммы… Сохранив октаву, он разделил ее на 12 равных частей. С введением этого строя в музыке восторжествовала темперация (от лат. - соразмерность)

Для построения гаммы необходимо было разделить ее на красиво звучащие части. Для её построения, оказывается, гораздо удобнее пользоваться логарифмами соответствующих частот: log2w0, log2w1… log2wm. Октава при этом перейдет в промежуток от log2w0 до log2 2w0 = log2w0 1, т. е. в промежуток длиной 1

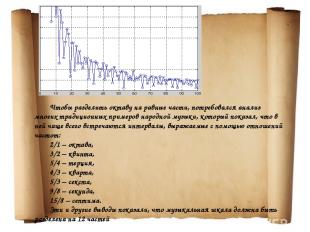
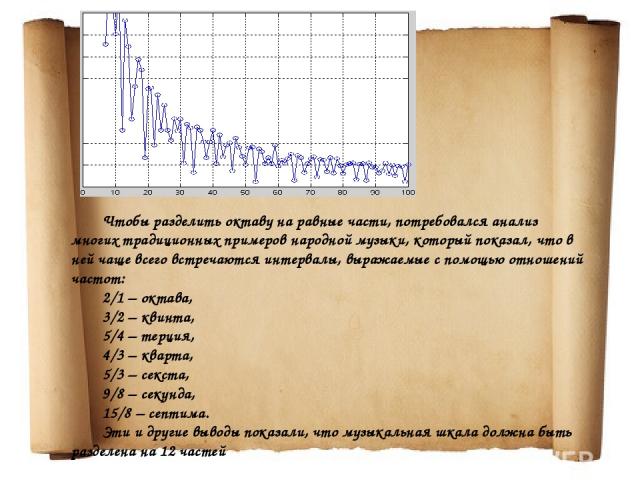
Чтобы разделить октаву на равные части, потребовался анализ многих традиционных примеров народной музыки, который показал, что в ней чаще всего встречаются интервалы, выражаемые с помощью отношений частот: 2/1 – октава, 3/2 – квинта, 5/4 – терция, 4/3 – кварта, 5/3 – секста, 9/8 – секунда, 15/8 – септима. Эти и другие выводы показали, что музыкальная шкала должна быть разделена на 12 частей

История создания равномерной темперации еще раз свидетельствует о том, как тесно переплетаются судьбы музыки и математики. Рождение нового музыкального строя не могло произойти без изобретения логарифмов и развития алгебры иррациональных величин. Без знания логарифмов провести расчеты равномерно-темперированного строя было бы невозможно. Логарифмы стали своеобразной «алгеброй гармонии», на которой выросла темперация

Терминология Последовательность В математике с понятием последовательность мы встречаемся крайне часто. Обычно цель при встрече с ними – отгадать следующее число или символ (поскольку последовательность в математике – упорядоченный ряд символов). Суть – найти закон, которому подчиняется данная последовательность. Например: 991, 19, 10, 1, 1, 1… 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Особенными последовательностями математики являются прогрессии – арифметическая и геометрическая (впрочем, с понятием прогрессия нередко можно встретиться и в жизни)

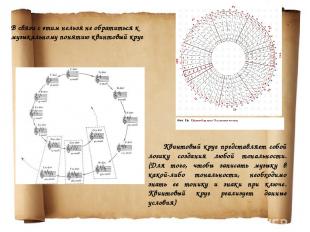
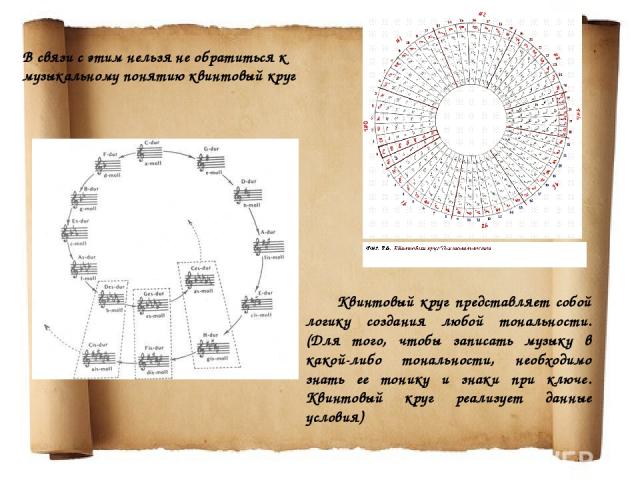
В связи с этим нельзя не обратиться к музыкальному понятию квинтовый круг Квинтовый круг представляет собой логику создания любой тональности. (Для того, чтобы записать музыку в какой-либо тональности, необходимо знать ее тонику и знаки при ключе. Квинтовый круг реализует данные условия)

Описанная прогрессия применена в музыке И. С. Баха, В. А. Моцарта, Л. В. Бетховена, что позволяет увидеть новую грань гениальности композиторов. Тот факт, что такая же прогрессия встречается и в современной русской и зарубежной музыке (практически во всех стилях), не наталкивает на мысль о гениальности, поскольку, проанализировав более 25 самых популярных на сегодняшний день мелодий, можно обнаружить не только прогрессии с разностью в квинту, но и в малую секунду, большую секунду, малую терцию, большую терцию и даже просто списанные друг с друга последовательности аккордов

Ритмы Слово «ритм» изначально принадлежало музыке, хотя сегодня неудивительно, что оно может быть известно человеку совершенно из других источников. Музыкальный ритм дается как пример, а не как определение. Таким образом, «ритм» можно назвать «интернациональным» в области науки и искусства

Математика также заимствовала данное слово. Исследуя математические закономерности и числовые последовательности, часто можно обнаружить ритмичность. В частности, «простейшими» примерами математических ритмов являются периодические дроби

Следует заметить, что без ритма музыка не смогла бы существовать. Она бы просто рассыпалась, так и не закончив ни одной музыкальной фразы

Рациональность и аффект Изучая попытки ученых связать математику и музыку воедино, можно говорить об эволюции понимания термина музыка. Абстрактным было понимание музыки в духе Пифагора и Платона, поскольку оно подразумевало именно математическое описание

Большие сомнения в простом тождестве аффекта и пропорции возникали достаточно давно. Встречаются они и в средние века. По Декарту способность органов чувств испытывать удовольствие относится к предпосылкам, которые теория музыки должна взять за основу. Она должна учитывать, что форма может быть трудной и разнообразной в той мере, в какой это отвечает естественным желаниям органов чувств

Математик из колумбийского университета Дж. Шиллингер в 1940 году опубликовал разработанную им математическую систему музыкальной композиции в виде отдельной книжечки под названием «Калейдофон». Считают, что Дж. Гершвин, работая над оперой «Порги и Бесс», пользовался той же системой. В 1940 году Эйгор Вилли Лобос, используя описанный способ, превратил силуэт Нью-Йорка в пьесу для фортепиано

Заключение Ученые всего мира изучают поистине интереснейшую проблему взаимосвязи математики и музыки. Таким образом, математики и музыканты могли осуществлять связь миров: опосредованного, материального и духовного, чувственного. О взаимосвязях математики и музыки можно говорить бесконечно долго, открывая все новые и новые, неожиданные и часто странные, одинаковые определения, понятия и смыслы. Безусловно, в данной работе была освещена лишь небольшая часть того неизведанного огромного мира связи музыки и математики, но мы будем разрабатывать и дополнять наш проект

Результаты Расширили свои познания о взаимосвязи музыки и математики 2) Познакомились с открытием диатонической шкалы Пифагором 3) Узнали о гениальном решении А.Веркмайстера 4) Рассмотрели связь логарифмов и музыки