Презентация на тему: Умножение отрицательных чисел




Формировать у учащихся предусмотренные программой знания; Формировать у учащихся предусмотренные программой знания; Начать работу по формированию умения умножать отрицательные числа; Продолжать работу по изучению истории математики.

Правила действий с обыкновенными и десятичными дробями. Правила действий с обыкновенными и десятичными дробями. Определение модуля числа.

« Минус на минус – всегда только плюс. Отчего так бывает, сказать не берусь». Английский поэт У.Г.Орден

Понятно, как выполнить действие Понятно, как выполнить действие (-7) * 3 = = (-7) + (-7) +(-7) = = -21
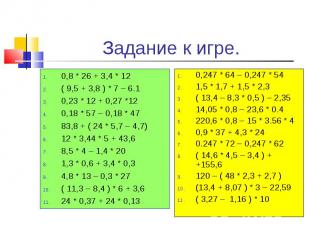
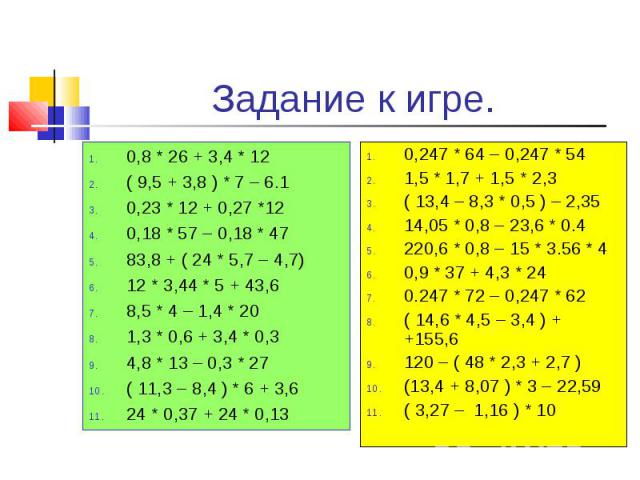
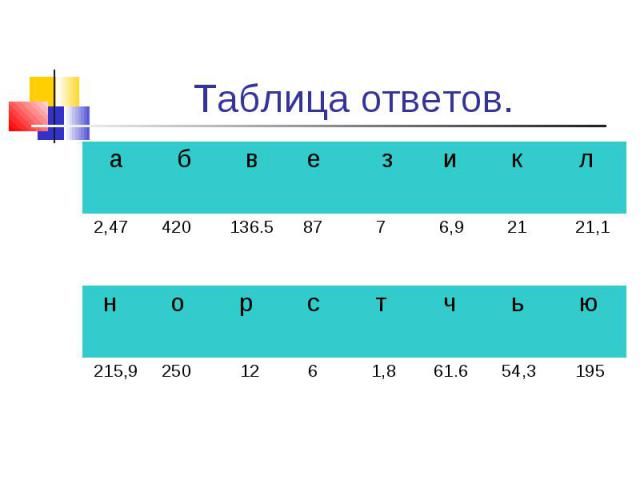
0,8 * 26 + 3,4 * 12 0,8 * 26 + 3,4 * 12 ( 9,5 + 3,8 ) * 7 – 6.1 0,23 * 12 + 0,27 *12 0,18 * 57 – 0,18 * 47 83,8 + ( 24 * 5,7 – 4,7) 12 * 3,44 * 5 + 43,6 8,5 * 4 – 1,4 * 20 1,3 * 0,6 + 3,4 * 0,3 4,8 * 13 – 0,3 * 27 ( 11,3 – 8,4 ) * 6 + 3,6 24 * 0,37 + 24 * 0,13

( 12,7 + 6,8 ) * 10 ( 12,7 + 6,8 ) * 10 ( 8,53 – 4,33 ) * 100 ( 24,83 – 22,33 ) * 100 ( 12,3 – 6,9 ) + 81,6
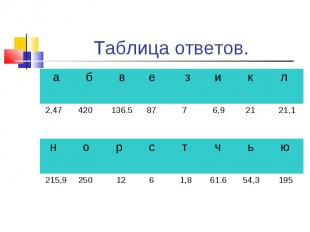

«Честность красит звание любое.» Ф. Шиллер

Брамагупта – индийский математик. Брамагупта – индийский математик. Жил в VII веке. Отрицательные числа представлял как «долги», положительные – как «имущества».

« Сумма двух имуществ – имущество»: « Сумма двух имуществ – имущество»: (+Х) + (+Х) = (+Х) « Сумма двух долгов есть долг»: (-Х) + (-Х) = (-Х)

Также в древности положительное число связывали со словом «друг», а отрицательное число со словом «враг». Также в древности положительное число связывали со словом «друг», а отрицательное число со словом «враг». На этом языке сформулировано правило умножения. Современное правило по сути не отличается от правил древности, но выражено другими словами.

Друг моего друга – мой друг: (+)*(+)=(+) Друг моего друга – мой друг: (+)*(+)=(+) Друг моего врага – мой враг:(+)*(–)=(–) Враг моего друга – мой враг:(–)*(+)=(–) Враг моего врага – мой друг:(–)*(–)=(+)