Презентация на тему: Демоверсия ГИА 2011 год

Демоверсия ГИА 2011 год Учитель ОУ СОШ №19Лурда Л.Н.

ЗАДАНИЕ № 1 Площадь территории Испании составляет 506 тыс. км2. Как эта величина записывается в стандартном виде?1) 5,06 · 102 км22) 5,06 · 103 км23) 5,06 · 104 км24) 5,06 · 105 км2

ЗАДАНИЕ № 2 Из 59 девятиклассников школы 22 человека приняли участие в городскихспортивных соревнованиях. Сколько приблизительно процентовдевятиклассников приняли участие в соревнованиях?1) 0,37 % 2) 27 % 3) 37 % 4) 2,7 %

ЗАДАНИЕ № 3 Числа a и b отмечены точками на координатной прямой. Расположите впорядке возрастания числа 1, 1 и 1. a b

ЗАДАНИЕ № 4 Найдите значение выражения х4 + х3 – 1, при х=1 4 3Ответ: ________________________

ЗАДАНИЕ № 5 Из формулы периода обращения T= t Nвыразите время вращения t.Ответ: ________________________

ЗАДАНИЕ № 6 Какое из приведённых ниже выражений тождественно равно произведению (x − 4)(x − 2) ?1) (x − 4)(2 − x)2) −(x − 4)(2 − x)3) (4 − x)(x − 2)4) −(4 − x)(2 − x)

ЗАДАНИЕ № 7 Представьте выражение 6m + 3-7m2 m в виде дроби. Ответ: ________________________

ЗАДАНИЕ № 8 Какое из данных выражений не равно выражению2 5 320 3 2010 3 520 3

ЗАДАНИЕ № 9 Решите уравнение x2 + 7x −18 = 0.Ответ: ________________________

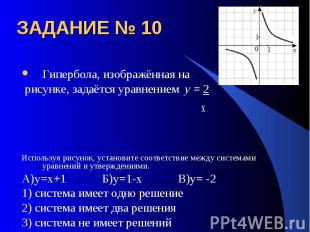
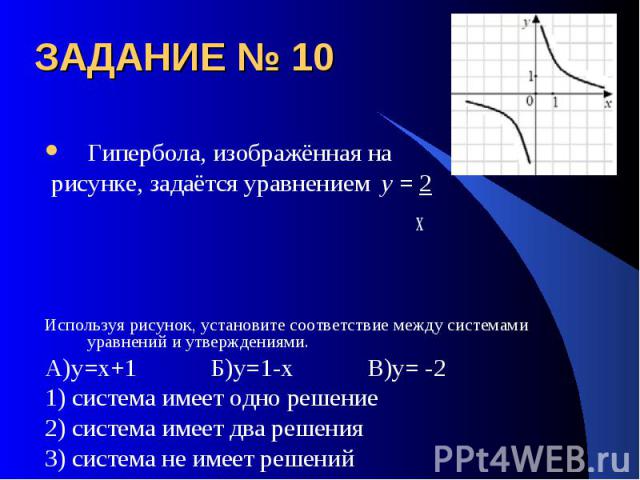
ЗАДАНИЕ № 10 Гипербола, изображённая на рисунке, задаётся уравнением y = 2 х Используя рисунок, установите соответствие между системами уравнений и утверждениями.А)у=х+1 Б)у=1-х В)у= -21) система имеет одно решение2) система имеет два решения3) система не имеет решений

ЗАДАНИЕ № 11 Прочитайте задачу:«Фотография имеет форму прямоугольника со сторонами 10 см и 15 см. Её наклеили на белую бумагу так, что вокруг фотографии получилась белая окантовка одинаковой ширины. Площадь, которую занимает фотография сокантовкой, равна 500 см2. Какова ширина окантовки?»Пусть ширина окантовки равна х см. Какое уравнение соответствует условию задачи?1) (10 + 2x)(15 + 2x) = 5002) (10 + x)(15 + x) = 5003) 10 ⋅15 + (10x +15x) ⋅ 2 = 5004) (10 + 2x)(15 + x) = 500

ЗАДАНИЕ № 12 Решите неравенство 20 − 3( x + 5) <1− 7x .Ответ: ________________________

ЗАДАНИЕ № 13 При каких значениях х верно неравенство x2 + 2x − 3 < 0 ?Ответ: ________________________

ЗАДАНИЕ № 14 Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие a25 < 0.1) an = 2n 3) an = −2n +1002) an = −2n + 50 4) an = 2n −100

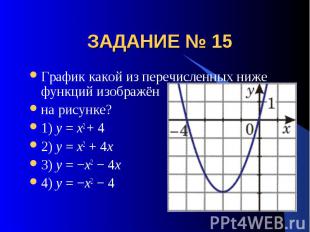
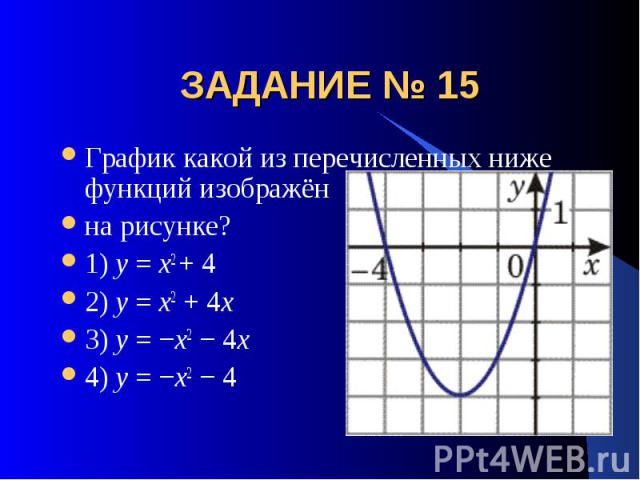
ЗАДАНИЕ № 15 График какой из перечисленных ниже функций изображённа рисунке?1) y = x2 + 42) y = x2 + 4x 3) y = −x2 − 4x4) y = −x2 − 4

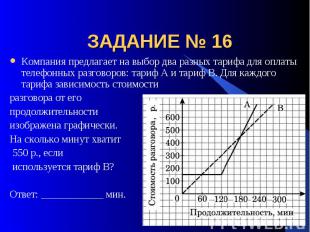
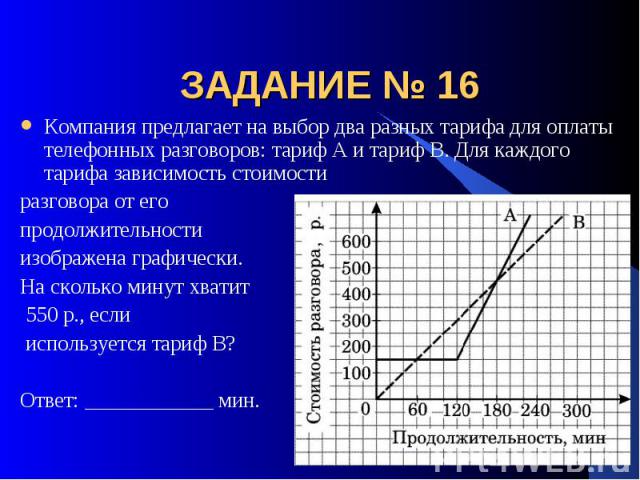
ЗАДАНИЕ № 16 Компания предлагает на выбор два разных тарифа для оплаты телефонных разговоров: тариф А и тариф В. Для каждого тарифа зависимость стоимостиразговора от его продолжительности изображена графически. На сколько минут хватит 550 р., если используется тариф В? Ответ: ____________ мин.

ЗАДАНИЕ № 17 На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку?Ответ: ________________________

ЗАДАНИЕ № 18 Записан рост (в сантиметрах) пяти учащихся: 158, 166, 134, 130, 132. На сколько отличается среднее арифметическое этого набора чисел от его медианы?Ответ: ________________________

ЗАДАНИЕ № 19 Решите уравнение x3 − 6x2 − 4x + 24 = 0 .

ЗАДАНИЕ № 20 Решите неравенство ( 19 − 4,5)(5 − 3x) > 0 .

ЗАДАНИЕ № 21 В геометрической прогрессии сумма первого и второго членов равна 108, а сумма второго и третьего членов равна 135. Найдите первые три члена этой прогрессии.

ЗАДАНИЕ № 22 Прямая y = 2x + b касается окружности x2 + y2 = 5 в точке с положительной абсциссой. Определите координаты точки касания.

ЗАДАНИЕ № 23 Из пункта А в пункт В, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта В вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от А до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки?