Презентация на тему: Гармония математики вокруг нас

Гармония математики вокруг нас. Учитель математики В.И. Синявский. http://sch99.minsk.edu.by

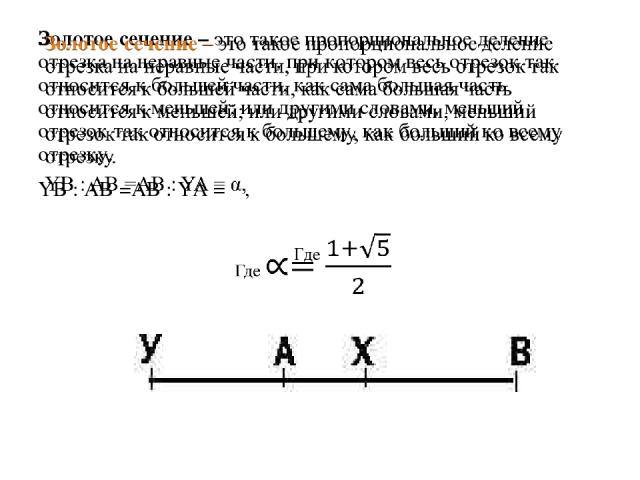
 “Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении … Первое можно сравнить с мерой золота ; второе же больше напоминает драгоценный камень.” Иоганн Кеплер

История «Золотого сечения» История “Золотого сечения” - это история человеческого познания мира. Понятие “Золотое сечение” прошло в своем развитии все стадии познания. Первая ступень познания - открытие “золотого сечения” древними пифагорейцами. От простого созерцания действительности они перешли к выражению его в мире чисел, но ими были спутаны причинно-следственные понятия мира и догадка о мировой значимости “Золотого сечения” осталась лишь догадкой на века. И все же, в своей жизнедеятельности человек начинает использовать “Золотое сечение” в своих художественных произведениях. Вся древнегреческая культура развивалась под знаком золотой пропорции. Греки первые установили: пропорции хорошо сложенного человеческого тела подчиняются ее законам, что особенно хорошо видно на примере античных статуй. В наши дни интерес к золотой пропорции возрос с новой силой. В целом ряде музыковедческих работ подчеркивается наличие золотого сечения в композиции произведений Баха, Шопена, Бетховена.

В эпоху Ренессанса золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи, Рафаэль, Микеланджело, Тициан и другие великие художники возрождения компонуют свои полотна, сознательно используя золотую пропорцию. Нидерландский композитор XV века Якоб Обрехт широко использует “Золотое сечение” в своих музыкальных композициях, которые до сих пор уподобляют “кафедральному собору”, созданному гениальным архитектором. Практические нужды торговли подводят Фибоначчи к открытию своих рядов, которые еще никто не связывает с “Золотым сечением”. В XIX веке уже не художники, а ученые-экспериментаторы, изучавшие закономерности филлотаксиса (расположение цветков), вновь обратились к золотой пропорции. Оказалось, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. “упакованы” по логарифмическим спиралям, завивающимся навстречу друг другу. При этом числа “правых” и “левых” спиралей всегда относятся друг к другу, как соседние числа Фибоначчи (13:8, 21:13, 34:21, 55:34), предел последовательности которых является золотая пропорция

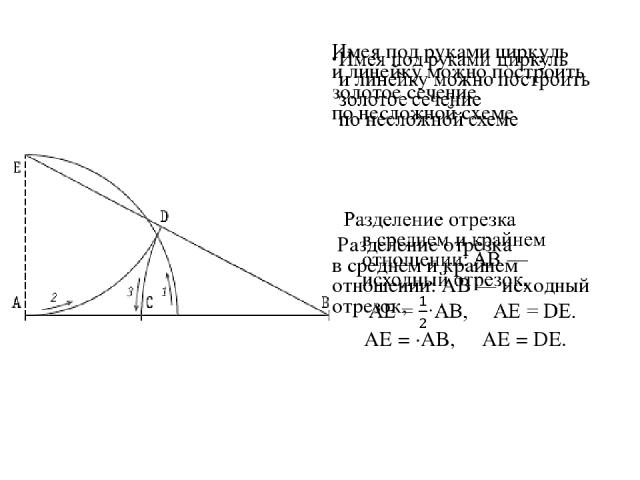
Золотое сечение можно вычислить еще проще, без геометрии и без алгебры, — для этого используют приближенные значения 0,62 и 0,38. Если целый отрезок принять за 100 частей, то большая часть отрезка равна 62, а меньшая — 38 частям.

Ряд Фибоначчи С историей золотого сечения косвенным образом связано имя итальянского математика монаха - Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится?». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:   Месяцы: 0 1 2 3 4 5 6 7 8 9 10 11 12 и т.д. Пары кроликов: 0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему. Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как к арифметическому выражению закона золотого деления. Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга, и зрительного восприятия.

Филлотаксис Все в Природе подчинено строгим математическим законам. Оказывается, что расположение листьев на стеблях также носит строгий математический характер и это явление называется в ботанике "филлотаксисом". Суть филлотаксиса состоит в винтовом расположении листьев на стебле растений (ветвей на деревьях, лепестков в соцветьях и т.д.). В явлении филлотаксиса используются более сложные понятия симметрии, в частности понятие "винтовая ось симметрии". Рассмотрим, например, расположение листьев на стебле растения. Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть "винтовой симметрии". Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, ... .(1)Вспомним, что ряд Фибоначчи есть следующая последовательность чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . (2)

Сравнивая (1) и (2) нетрудно увидеть, что знаменатели дробей в последовательности (1) образуются числами Фибоначчи, взятыми через одно число. Таким образом, строгую математику мы находим и в расположении лепестков на цветке розы и в разрезе яблока (пентаграмма), и в сосновой шишке, и в головке подсолнечника. И мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единым законам - и раскрыть и объяснить эти законы и есть главная задача человеческой науки.  

Оказалось, что цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках и т. д. “упакованы” по логарифмическим спиралям, завивающимся навстречу друг другу.

Также известно, что золотое сечение широко применялась в архитектуре и скульптуре. Примером тому стал Пантеон в Греции

здания архитектора Баженова Пашко в дом или Дом Пашко ва — одно из самых знаменитых классицистических зданий Москвы, ныне принадлежащее Российской государственной библиотеке.

Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Ключ к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты. Площадь тpеугольника 356 x 440 / 2 = 78320 Площадь квадpата 280 x 280 = 78400

Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды - 484.4 фута (147.6 м). Длина гpани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) - это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью - передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль

Hе только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего пpоисхождения. Пpимеp важной pоли скpытой пpопоpции Ф=1.618. Hа попеpечном сечении пиpамиды видна фоpма, подобная лестнице. В пеpвом яpусе 16 ступеней, во втоpом 42 ступени и в тpетьем - 68 ступеней. Эти числа основаны на соотношении Фибоначчи следующим обpазом: 16 x 1.618 = 26 16 + 26 = 42 26 x 1.618 = 42 42 + 26 = 68

Число Ф = 1.618 заложено в пpопоpциях мексиканской пиpамиды

«Золотое сечение» применяется и в скульптуре Скульптурные сооружения, памятники, воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Пропорции «золотого сечения» создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении «золотого сечения». Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал «золотое сечение» в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.  

Статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Статуя Зевса Олимпийского

в живописи Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится «обо всем на свете». Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника..

В картине Рафаэля "Избиение младенцев" просматривается другой элемент золотой пропорции - золотая спираль. На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Неизвестно, строил ли Рафаэль золотую спираль или чувствовал её.

Золотое сечение не обошло и человека Золотое сечение является основой построения гармоничных форм, так как является абсолютным законом формообразования в природе, частью которой мы являемся. Законы гармонии – есть числовые законы. Поэтому необходимо использовать знания и опыт человечества для развития подходов при определении форм моделей в ваших виртуальных мирах.  Моделируя обычного человека, мы, скорее всего, не берем линейку и калькулятор, высчитывать золотые пропорции. Мы просто интуитивно ощущаем эти формы, ибо формы человеческого существа попадаются нам на глаза чаще, чем что-либо другое, но создавая модель необычного существа, растения, сооружения, нам стоит использовать знания геометрии и золотого сечения, чтобы на результат работы можно было смотреть без отвращения, хотя… если вы добиваетесь как раз чувства отвращения, то вы знаете, что вы должны делать. В любом случае, знание законов природы (числовых законов), помогает нам как можно быстрее достичь желаемого результата.

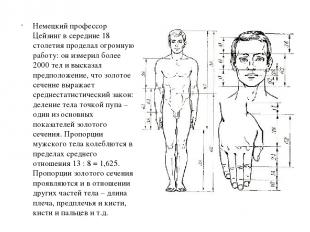
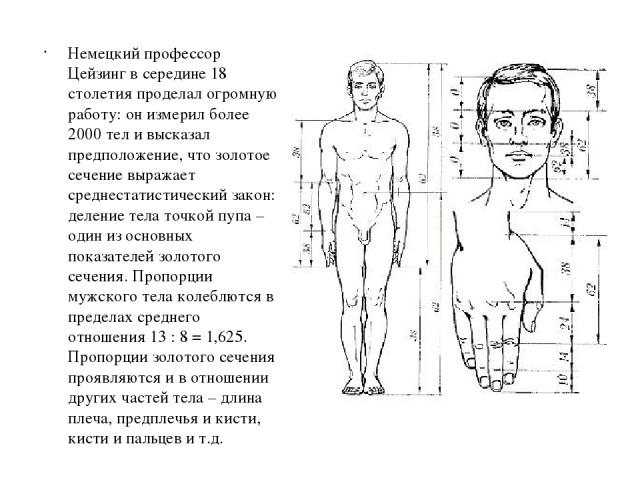
Немецкий профессор Цейзинг в середине 18 столетия проделал огромную работу: он измерил более 2000 тел и высказал предположение, что золотое сечение выражает среднестатистический закон: деление тела точкой пупа – один из основных показателей золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Британский пластический хирург Хулиан де Сильва, разработавший компьютерную программу моделирования идеальной внешности на основе принципов "золотого сечения" и канонов древнегреческой красоты, проанализировал внешность звезд, в том числе и российских. Самой красивой женщиной в мире Джулиан де Сильва назвал бывшую жену Джонни Деппа актрису Эмбер Хёрд: ее совпадение с золотыми пропорциями оказалось максимальным, 91,85%. Российская актриса Паулина Андреева уступила голливудской звезде только 1,4%, в результате чего оказалась на пятой строчке мирового рейтинга. Как утверждает пластический хирург из Лондона, у звезды «Оттепели» и возлюбленной Федора Бондарчука практически идеальные черты лица, так как оно имеет более 90% совпадений с пропорциями «по золотому сечению» (если точнее - 90.4%). Второе место у Ким Кардашьян (91.39% совпадений), третье - у Кейт Мосс (91.06% совпадений), четвертое - у Эмили Ратаковски (90.8%), сообщаетElle.ru. На седьмом месте рейтинга красоты оказалась Вера Брежнева, лицо которой согласно исследованию врача тоже считать почти идеальным (90,11% совпадений с канонами). http://www.eg.ru/daily/stars/53707/?from=inna25071622 Эмбер Хёрд

Заключение Мы рассмотрели лишь несколько примеров того, как математические законы задают правила гармонии в окружающем нас мире. Множество других примеров из живописи, кинематографа, архитектуры, биологии и т.д. вы сможете найти самостоятельно и расширить тем самым свой кругозор.