Презентация на тему: Термодинамический и статистический методы

Статистический и термодинамический методы Идеальный газ 900igr.net

Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах. Первый шаг в познании строения вещества – установить из каких частей состоят тела, и как они взаимодействуют между собой. Два метода изучения макроскопических тел, состоящих из большого числа частиц: 1. статистический (молекулярно-кинетический), 2. термодинамический.

Большое число частиц: при нормальных условиях (р0 = 1,013·105 Па, Т0 = 273,15 К) все газы содержат в единицы объёма одинаковое число молекул NЛ = 2,68·1025 м-3 – число Лашмидта. При одинаковой температуре и давлении все газы содержат в единицы объёма одинаковое число молекул.

● Статистический метод В основе лежит модель, которая описывается уравнениями теории вероятности и математической статистики. Основываясь на молекулярно-кинетических представлениях о веществе (все тела состоят из молекул, находящихся в непрерывном хаотическом движении), сформулированы статистические распределения.

Статистические распределения: 1. распределение молекул по объёму – n = const, 2. распределение молекул по скоростям –распределение Максвелла, 3. распределение молекул по потенциальным энергиям – распределение Больцмана, 4. закон равномерного распределения энергии по степеням свободы. Из этих распределений получают средние значения физических величин, которые характеризуют состояние системы.

● Термодинамический метод В основе лежат опытные факты, проверенные человеком. Достоверность этого метода выше. Метод изучает общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.

Основные законы термодинамики: • I начало термодинамики – закон сохранения энергии тепловых процессов. dQ – тепло, подводимое к системе, dU – внутренняя энергия системы, dA – работа, совершаемая системой.

Основные законы термодинамики • II начало термодинамики – характеризует направление протекания процессов, дополняет I начало термодинамики. Формулировка Клаузиуса (1850 г.): тепло не может самопроизвольно переходить от тела, менее нагретого, к телу, более нагретому. Для кругового процесса: А – совершаемая работа, ∆Q – количество тепла, отнятое от нагревателя.

Основные законы термодинамики • III начало термодинамики: абсолютный нуль температуры недостижим – теорема Нернста. Абсолютный нуль температуры – температура, при которой прекращается хаотическое движение молекул.

Термодинамическая система – совокупность макроскопических тел, которые обмениваются энергией, как между собой, так и с внешними телами (внешней средой). Одно макроскопическое тело это уже термодинамическая система.

Состояние термодинамической системы характеризуется (задаётся) совокупностью физических величин (параметров состояния), называемых макроскопическими термодинамическими параметрами: р, T, V, ρ. Если термодинамические параметры с течением времени не меняются, то говорят, что система находится в состоянии термодинамического равновесия – р = const, T = const.

Для анализа состояния системы используется уравнение состояния: р = f(V,T) – функциональная зависимость равновесного давления от других термодинамических параметров.

Единица количества вещества. Число Авогадро 1 моль – количество вещества, в котором содержится такое же число атомов, молекул и других структурных элементов, сколько атомов содержится в нуклиде 12С массой 0,012 кг. Число Авогадро NA = 6,02·1023 1/моль. Нуклиды – общее название ядер, отличающихся числом нейтронов N и протонов Z. Молярная масса – масса вещества, взятого в количестве одного моля: M = m· NA  [кг/моль].

Молекулярно-кинетическая теория идеального газа. Основные положения 1. Все тела состоят из атомов и молекул. 2. Атомы и молекулы находятся в непрерывном беспорядочном (хаотичном) движении. Твёрдое тело сохраняет форму и объём. Жидкость – объём. Газ не сохраняет форму и объём. 3. Между атомами и молекулами действуют силы взаимодействия – силы притяжения и отталкивания.

• Понятие об идеальном газе Идеальный газ – модель. 1. Собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда. → Молекула – материальная точка. 2. Между молекулами газа отсутствуют силы взаимодействия. 3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Следовательно, идеальный газ – система независимых материальных точек.

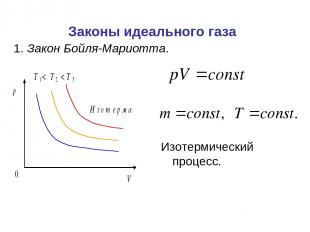
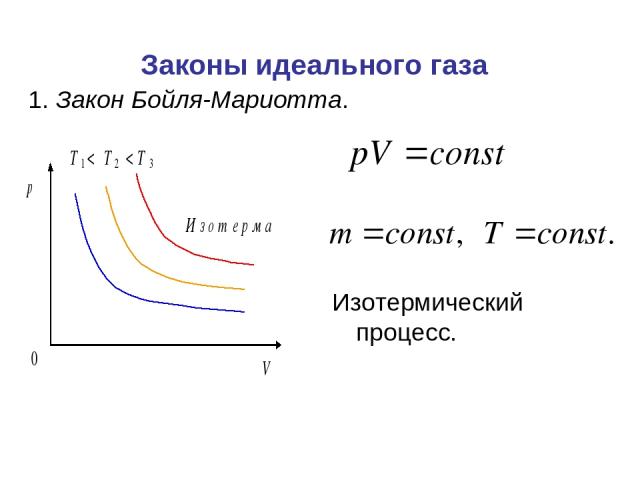
Законы идеального газа Изотермический процесс. 1. Закон Бойля-Мариотта.

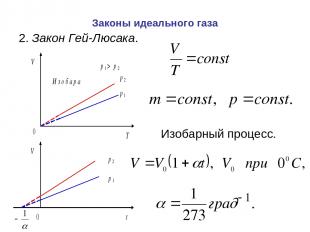
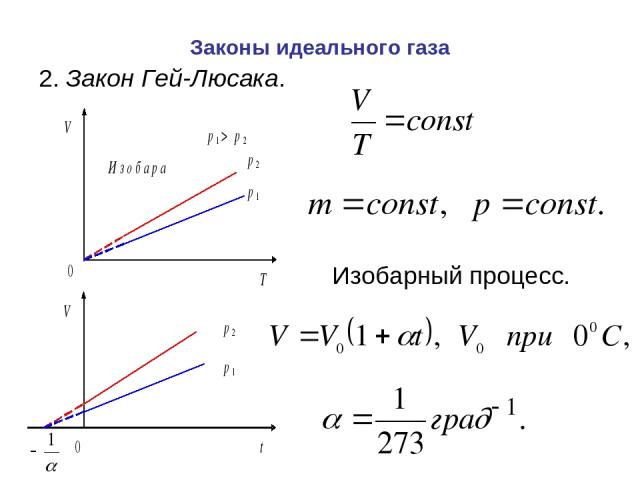
Законы идеального газа Изобарный процесс. 2. Закон Гей-Люсака.

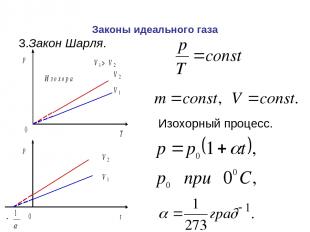
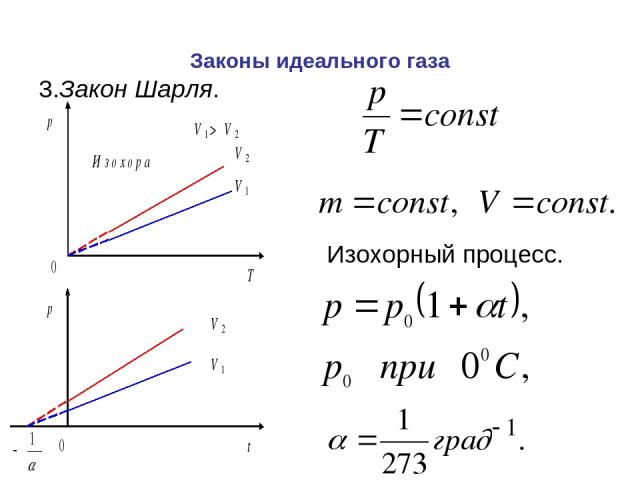
Законы идеального газа Изохорный процесс. 3.Закон Шарля.

Законы идеального газа 4. 5. Закон Авогадро – моли любых газов при одинаковой температуре и давлении занимают одинаковые объёмы. При нормальных условиях он равен

Законы идеального газа 6. Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в неё газов. Парциальное давление – давление, которое бы производил газ, входящий в состав газовой смеси, если бы он один занимал весь объём, в котором находится смесь.

Законы идеального газа Уравнение Клайперона-Менделеева – уравнение состояния для газа массы m: количество вещества, молярная универсальная газовая константа. постоянная Больцмана.

Запишем уравнение (1) для 1 моля газа: концентрация молекул. ρ – плотность вещества:

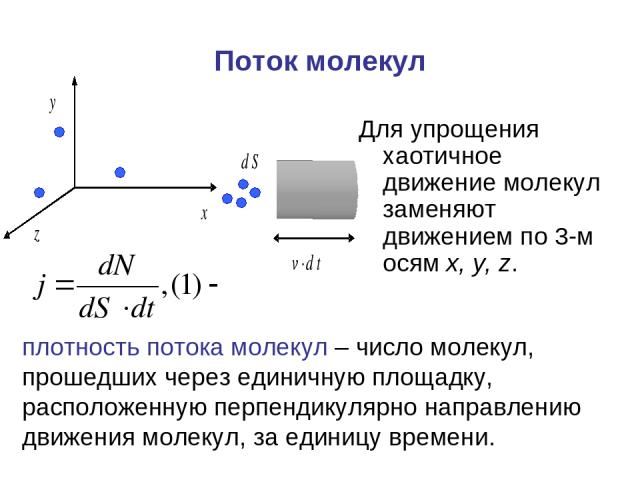
Поток молекул Для упрощения хаотичное движение молекул заменяют движением по 3-м осям x, y, z. плотность потока молекул – число молекул, прошедших через единичную площадку, расположенную перпендикулярно направлению движения молекул, за единицу времени.

Поток молекул Примем 1. все молекулы имеют одинаковую скорость v, 2. молекулы движутся только вдоль координатных осей x, y, z. Т.к. пространство изотропно, то вдоль каждой из осей могут двигаться 1/3 всех молекул, находящихся в объёме. При этом половина этого числа может двигаться в положительном направлении оси, другая половина – в отрицательном направлении.

Поток молекул n – концентрация молекул. число молекул в объёме dV. число молекул, движущихся в положительном направлении одной из осей. Уравнении (3) подставляем в (1): плотность потока молекул. в векторном виде.

Поток молекул Если ввести понятие средней скорости, и всё учесть, то

Уравнение Клаузиуса – основное уравнение молекулярно-кинетической теории идеального газа давление газа на стенку. Если газ состоит из N молекул, движущихся со скоростями v1, v2 …vn, то вводится понятие средней квадратичной скорости: Уравнение Клаузиуса связывает характеристики макромира (р) с характеристиками микромира (v).

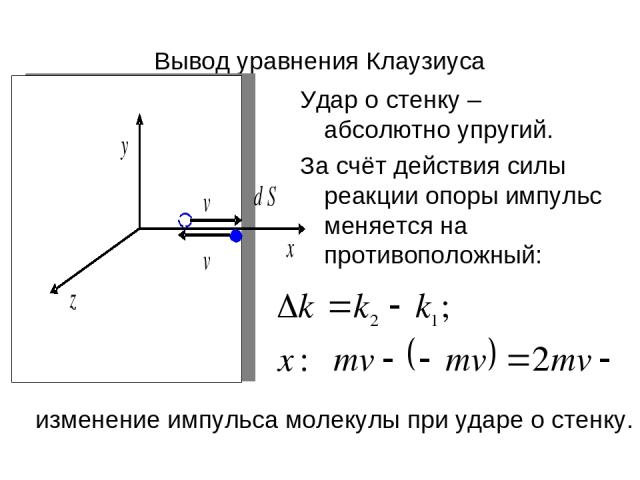
Вывод уравнения Клаузиуса Удар о стенку – абсолютно упругий. За счёт действия силы реакции опоры импульс меняется на противоположный: изменение импульса молекулы при ударе о стенку.

Уравнение Клаузиуса По закону сохранения импульса молекула при ударе о стенку передаёт стенке импульс Импульс, переданный площадке dS за время dt: По 2 закону Ньютона: Уравнение (2)=(1):

Уравнение Клаузиуса Если молекулы движутся с разными скоростями, то переходят к Средняя кинетическая энергия молекул

Следствия из уравнения Клаузиуса 1. Внутренняя энергия идеального газа. В сосуде N молекул, каждая обладает энергией Внутренняя энергия:

Следствия из уравнения Клаузиуса 2. Абсолютная температура – мера интенсивности хаотического движения атомов и молекул. Подставляем в (1):

Подставляем в (1): Абсолютная температура – мера энергии хаотического движения (мера интенсивности хаотического движения).

Следствия из уравнения Клаузиуса 3. Другой вид уравнения.