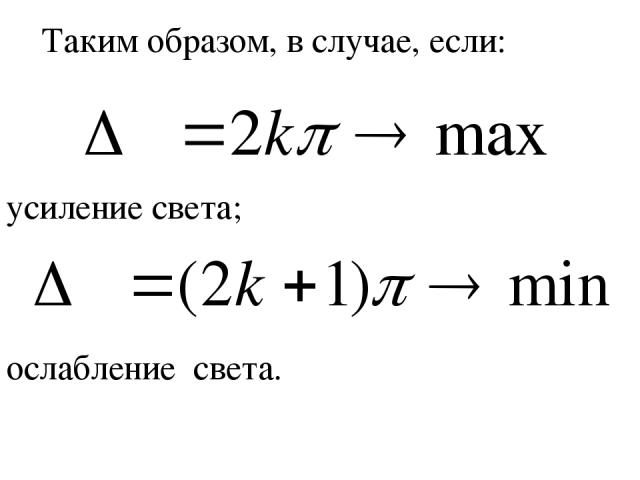Презентация на тему: Световая волна

ВОЛНОВАЯ ОПТИКА Световая волна. Интенсивность света Интерференция света Получение когерентных световых волн Опыт Юнга Интерференция света в тонкой плоскопарал-лельной пластинке (плёнке) Полосы равной толщины и равного наклона Кольца Ньютона Условия наблюдения интерференции в тонких плёнках Практические приложения интерференции 900igr.net

1. Световая волна. Интенсивность света Волновая оптика –это раздел оптики, в котором изучается круг явлений с точки зрения волновой природы све-та. Максвелл (1831 – 1879), обобщая законы электромагнетизма, пришел к выводу об электромагнитной природе света. В электромагнитной волне колеблются векторы и . Фзиологические, фотохими-ческие, фотоэлектрические и другие действия света вызываются колебаниями электрического вектора . В дальнейшем мы будем называть его

световым вектором. Изменение его модуля во времени и пространстве представляет волновой процесс и описывается с электромагнитной точки зрения уравнением: или (1) (2) В (1) и (2) - расстояние, отсчитываемое вдоль направления распространения световой волны.

то - длина световой волны, Отношение называется абсолютным показателем преломления среды. - её фазовая скорость. (3) Так как, согласно электромагнитной теории Максвелла Для большинства прозрачных веществ практически не отличается от единицы, поэтому (4)

Заметим, что получено на основе измерений, выполненных в быстропротекающих электриче-ских полях, т.е зависит от частоты. Следова-тельно, и показатель преломления зависит от частоты, т.е. - дисперсия света. Диапазон видимой области спектра определяется физиологической чувствительностью глаза и нахо-дится в пределах длин волн ~ 390 ÷ 760 нм. Эти значения относятся к световым волнам в вакууме. В веществе длины волн будут иными. В случае колебаний частоты в вакууме: (5)

в среде, в которой фазовая скорость волны длина волны имеет значение (6) Таким образом, длина световой волны в среде с показателем преломления связана с длиной волны в вакууме соотношением: (7) Диапазон частот видимой области спектра лежит в пределах (4 ÷ 7,5)·1014 Гц. Это огромная частота. Ни глаз, ни какой-либо приемник световой энергии не могут уследить за столь частыми изме-

нениями световой энергии. Они регистрируют усредненный поток энергии.скольку световая волна имеет электромагнитную природу, то как мы уже показали ранее: или, учтя что получаем: ~ (8) В изотропной среде показатель преломления одинаков по всем направлениям. Поэтому ~

2. Интерференция света Интерференция света – это явление усиления или ослабления света в результате сложения когерентных световых волн. Когерентные волны – это волны, имеющие: 1) одинаковую частоту; 2) постоянную во времени в данной точке пространства разность фаз. При сложении в некоторой точке пространства когерентных волн амплитуда результирующего колнебания находится в результате геометриче- ского сложения амплитуд исходных колебаний: (9)

Можно, однако, условиться за меру интенсивно-сти света принимать квадрат амплитуды светового вектора т.е.: Тогда (9) можно записать в виде: Если разность фаз , то колебания когерентны и величина и, следовательно, т.е. имеет место нарушение закона геометрической (10)

оптики об аддитивности сложения интенсивностей световых пучков. Если в (9) то и тогда Пусть тогда или (11) Если в (9) то и тогда Пусть тогда

B b и, следовательно, (12) Таким образом, в результате сложения когерентных световых волн интенсивность света меняется в пределах (13) В случае некогерентных световых волн < > = 0 и, следовательно, в этом случае наблюдается аддитивное усиление света, т.е.

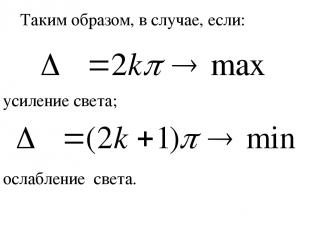
Таким образом, в случае, если: усиление света; ослабление света.

3. Получение когерентных световых волн Два метода получения КСВ: деление фронта световой волны; 2) деление амплитуды световой волны. После деления фронта или амплитуды световой волны возникшие КСВ до их встречи в некоторой точке наблюдения Р проходят разные пути и, возможно, в средах с различными показателями преломления. Рис. 1.

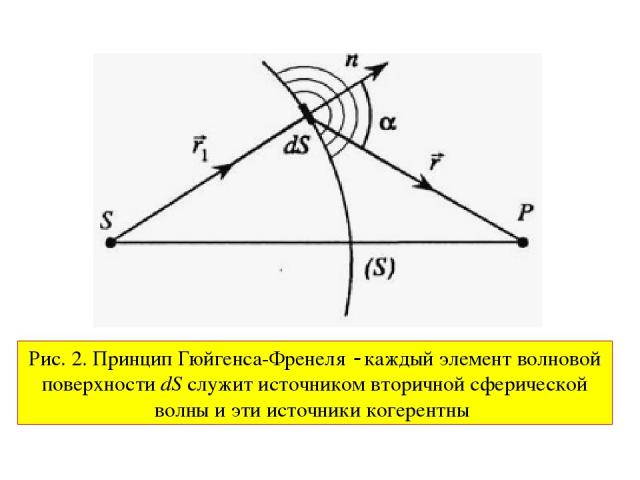
В XVIII столетии Гюйгенс сформулировал следующий принцип. Когда волновой фронт проходит одно или несколько отверстий, каждый элемент волнового фронта ведет себя так, как если бы он стал источником излучения - источником вторичных волн. Распределение интенсивности света на экране представляет собой такую же картину, как если бы щели были заменены источниками. Впервые такой эксперимент выполнил Юнг в 1803 г.

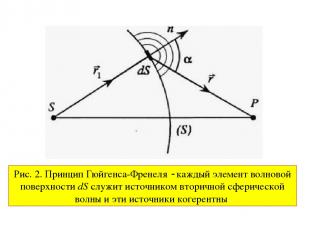
Рис. 2. Принцип Гюйгенса-Френеля каждый элемент волновой поверхности dS служит источником вторичной сферической волны и эти источники когерентны

Пусть точечный источник S возбуждает световую волну. Её фронт – поверхность сферы. Колебания от когерентных источников ΔS1 и ΔS2 достигают точки Р и складываются. Разность фаз (14) Рис. 3.

Здесь - геометрическая разность хода. Если световые волны от когерентных источни-ков ΔS1 и ΔS2 распространяются в средах с различ-ными показателями преломления, то разность фаз где Учтя это, имеем: Величина называется оптиче- ской разностью хода. - длина световой волны в вакуме. (15)

Выразим из (15) оптическую разность хода через разность фаз (16) Тогда условия усиления и ослабления света при интерференции можно представить в виде: (17) (18)

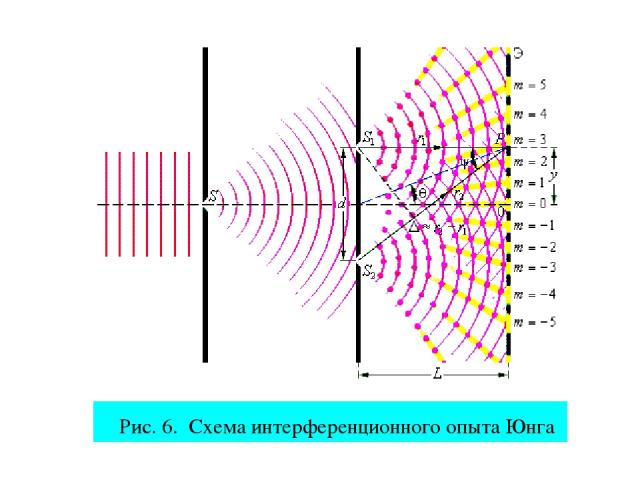
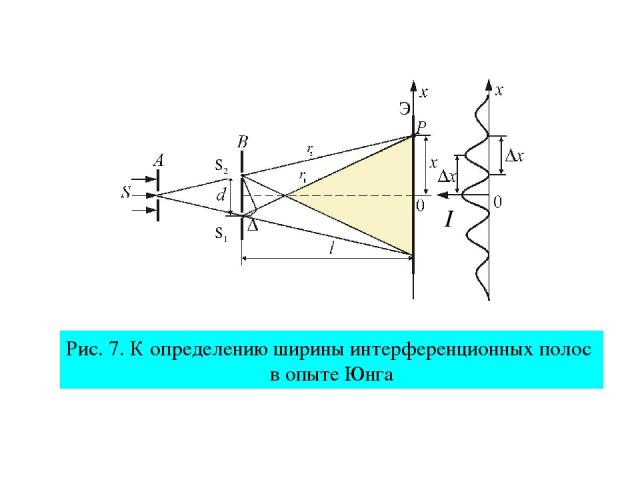
4. Опыт Юнга Рис. 4. На рис. 2 S1 и S2 - когерент-ные источники света, Э – экран, d – расстояние между щелями, x – координата интерференци-онного максимума или миниму-ма, r1 и r2 – оптические пути световых волн, приходящих в точку Р. Применяя к треугольникам PMS2 и PNS1 теоре-му Пифагора и пренебрегая членами второго по-рядка малости , находим, что: (19)

В опыте Юнга d

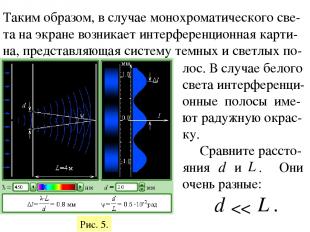
Таким образом, в случае монохроматического све-та на экране возникает интерференционная карти-на, представляющая систему темных и светлых по- лос. В случае белого света интерференци-онные полосы име-ют радужную окрас-ку. Сравните рассто-яния и . Они очень разные:

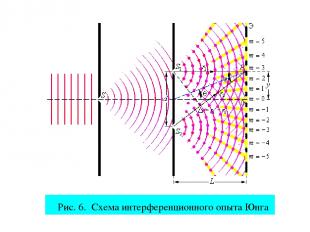
Рис. 6. Схема интерференционного опыта Юнга

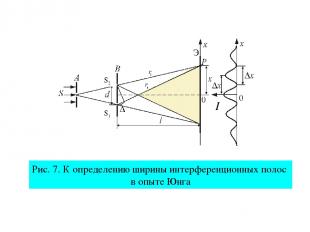
Рис. 7. К определению ширины интерференционных полос в опыте Юнга

Ширина интерференционной полосы или В любом случае, с учетом выражений (21) (22)

5. Интерференция света в тонкой плоскопарал- лельной пластинке (плёнке) Пусть пластинка с пока- pателем преломления n находится в воздухе. До встречи в точке С лучи S1 и S2 проходят разные оптические пути в раз- ных средах. Оптическая разность хода S1 и S2 - учитывает потерю полуволны при отражении луча S2 в точке С. (23) Рис. 8.

Из геометрических соображений находим AB и DC И подставляем в формулу (23). Получаем: Избавимся от угла β: Подставляя значения функций угла β в формулу (24) и выполняя необходимые действия, получаем: (24)

(24) Формула (24) представляет оптическую разность хода световых волн в отражённом свете. При освещении пластинки монохроматическим светом и выполнения условия усиления пластинка представляется глазу, при рассмотрении её под углом α, окрашенной в данный монохроматиче-ский свет. При выполнении условия ослабления пластинка представляется глазу темной.

При освещении пластинки белым светом и при выполнении условия усиления пластинка пред-ставляется глазу окрашенной в последовательные спектральные цвета, если угол α, под которым эта пластинка рассматривается, постепенно изменяет-ся. Если на плоскопараллельную пластинку падает свет под различными углами (напр., рассеянный свет или свет от точечного источника), то интерфе-ренционная картина в этом случае будет иметь вид 6. Полосы равной толщины и равного наклона

одним и тем же углом. С помощью собирающей линзы эти круговые полосы могут быть спроеци-рованы на экран. Они называются полосами рав-ного наклона и локализованы в бесконечности. чередующихся тёмных и светлых круговых полос с общим центром в точке О. Каждая из этих полос образована лучами, падающими на пластинку под Рис. 9.

Если, однако, пластинка (плёнка) не плоскопарал-лельна, если её толщина в различных местах разная, то и условия интерференции в этимх местах различны. Геометрическое место точек , в которых условие интерференции одинаково, соответствует местам, в которых пластинка имеет одинаковую толщину. Например, пленка в виде клина. При отражении (прохождении) света от такой плёнки интерференционная картина будет иметь вид чередующихся светлых и темных полос. Рис. 10.

Каждая такая полоса соответствует местам одинаковой толщины кли-на. Эти интерференционные поло-сы называют полосами равной тол-щины. Типичным примером полос рав-ной толщины являются кольца Ньютона. Найдём оптическую разность Рис. 11. хода , при которой возникает k-е кольцо Ньюто- тона. Из рис. 10 следует, что (24) (25)

Из этого же рисунка следует, что Подставляя в (25), получаем: (26) Радиусы светлых колец Ньютона: → Радиусы темных колец Ньютона: → (27) (28)

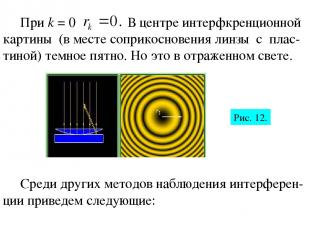
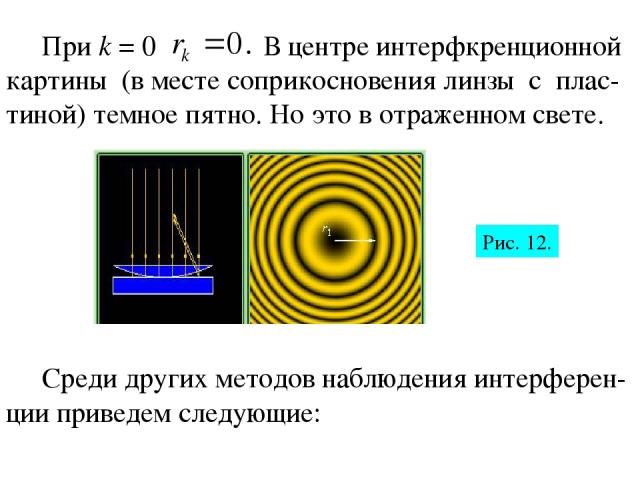
При k = 0 В центре интерфкренционной картины (в месте соприкосновения линзы с плас-тиной) темное пятно. Но это в отраженном свете. Среди других методов наблюдения интерферен-ции приведем следующие: Рис. 12.

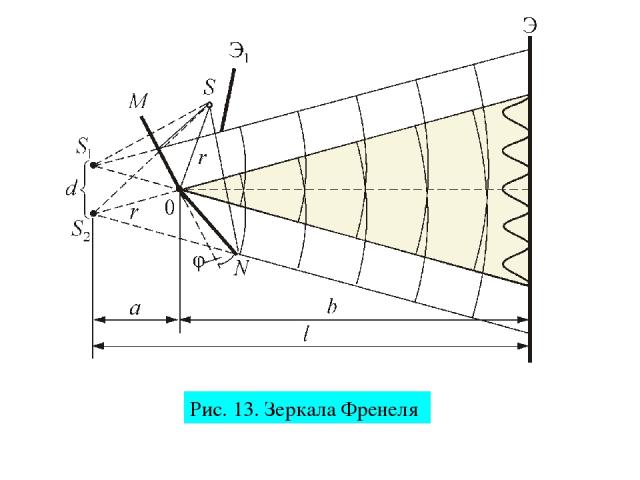
Опыт, аналогичный опыту Юнга, был осуществлен Френелем в 1816 г. Две когерентные световые волны получались в результате отражения от двух зеркал, плоскости которых наклонены под небольшим углом φ друг к другу (рис. 4). Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются, возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой (экраном Э1)

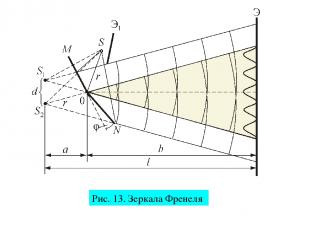
Рис. 13. Зеркала Френеля

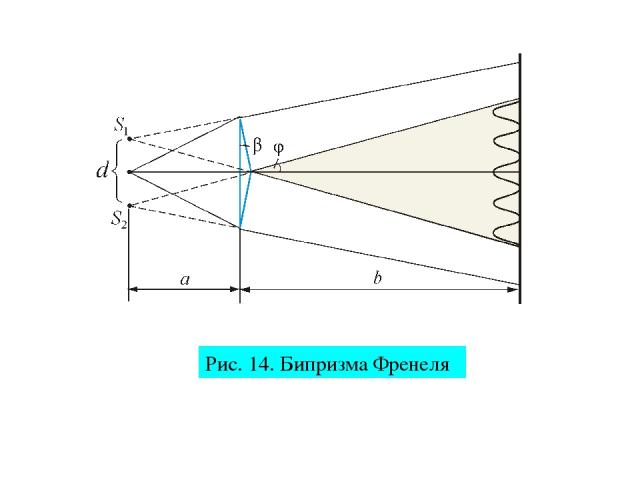
Бипризма Френеля В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180 . Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (рис. 5) Здесь образуются два близких мнимых изображения S1 и S2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол φ = (n - 1)β.

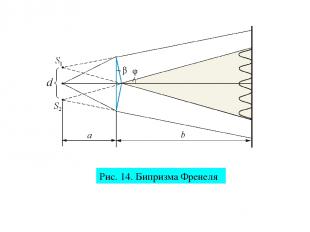
Рис. 14. Бипризма Френеля

7. Условия наблюдения интерференции в тонких плёнках Для наблюдения интерференции необходимо перекрытие волновых цугов. Цуги при выходе волн из точек А и В должны перекрываться. Необходимо, чтобы время запаздывания второго цуга по отно- шению к первому не превышало времени τког, назы-ваемого временем когерентности. τког = 10-8 с (вре-мя жизни атома в возбуждённом состоянии). Необходимо так же, чтобы оптическая разность хода была меньше, чем длина когерентности lког. Рис. 15.

(с – скорость света в вакуме). (полная интерференция) (частичная интерференция) (отсутствие интерференции) Возможно, что для наблюдается минимум, а для - максимум, т.е. Рис. 16. Рис. 17.

При λ1 = 560 нм и λ2 = 570 нм При α = 0º d ~ 10-5 м = 0,01 мм. Реально d на 2 ÷ 3 порядка меньше. Конец лекци по данной теме