Презентация на тему: Основные законы электротехники

Основные законы электротехники

Схема – это графическое изображение электрической цепи.Ветвь – это участок схемы, вдоль которого течет один и тот же ток. Узел – это место соединения трех или большего числа ветвей Контур – это замкнутый путь, проходящий по нескольким ветвям Независимый контур – это контур, у которого хотя бы одна ветвь не принадлежит другим контурам

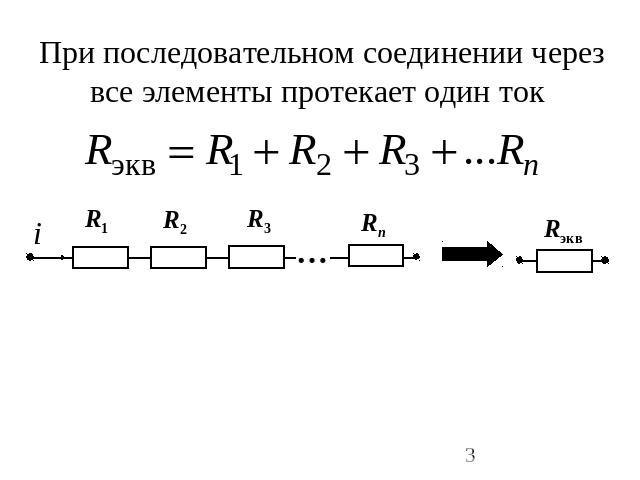
При последовательном соединении через все элементы протекает один ток

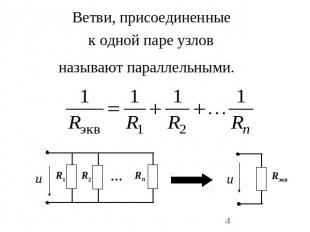
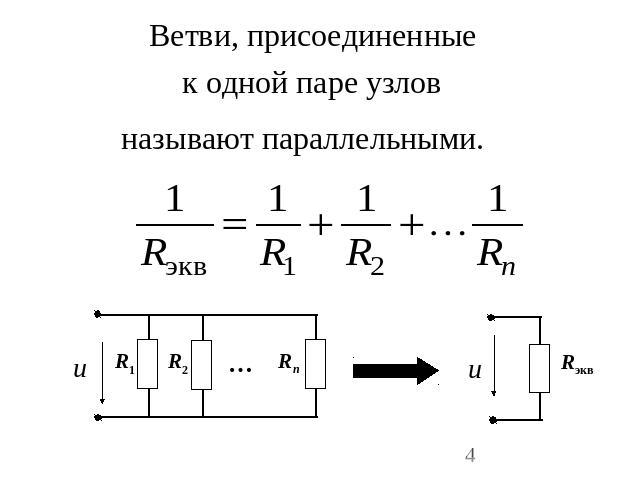
Ветви, присоединенныек одной паре узловназывают параллельными.

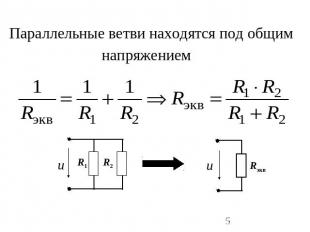
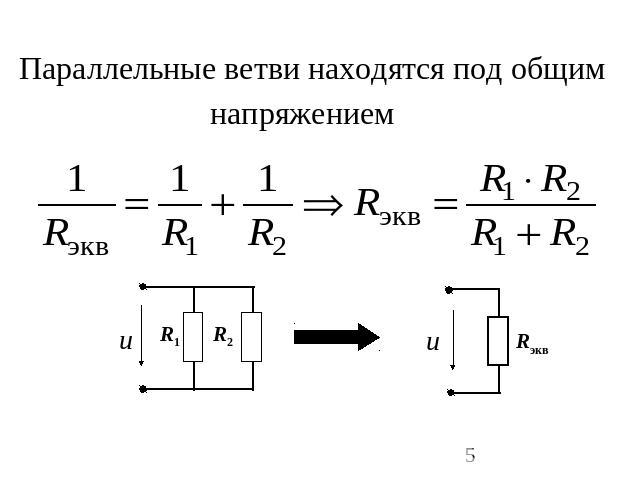
Параллельные ветви находятся под общим напряжением

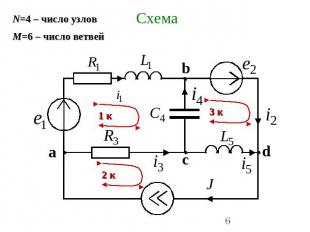
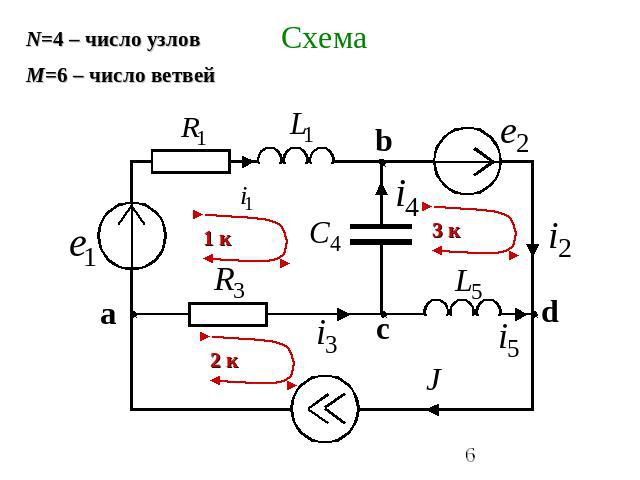
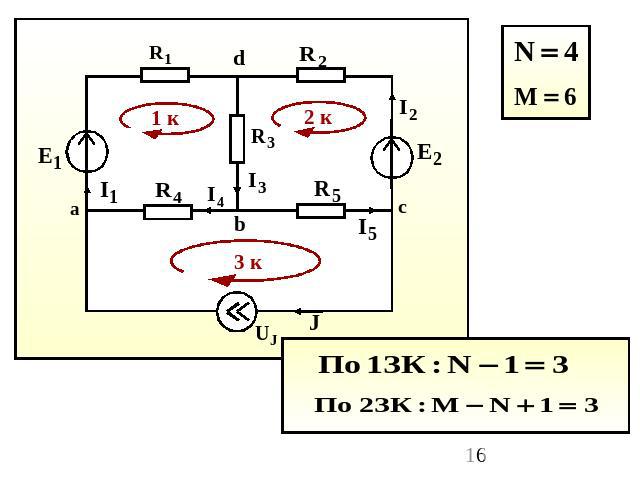
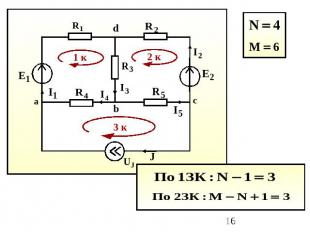
Схема N=4 – число узлов М=6 – число ветвей

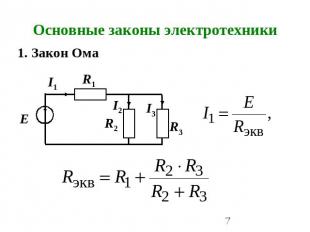
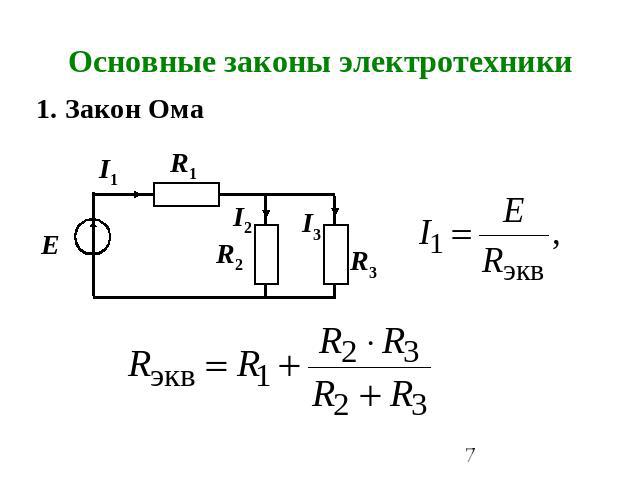
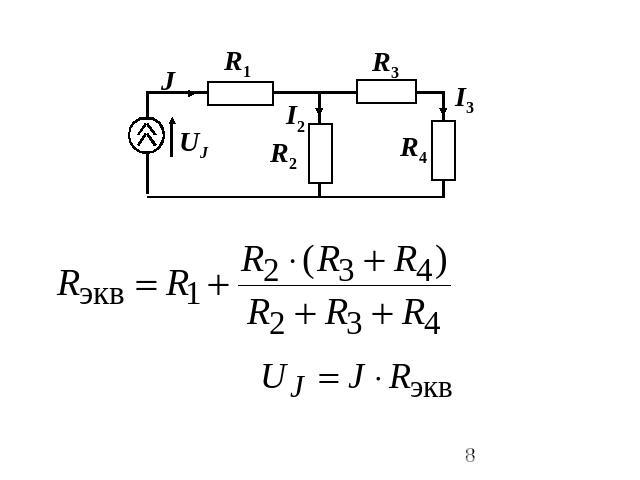
Основные законы электротехники 1. Закон Ома

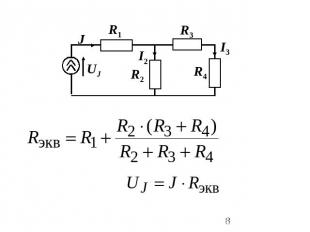
Законы Кирхгофа Кирхгоф (Kirchhoff) Густав Роберт 1824-1887г.немецкий физик, член Берлинской АН, член-корреспондент Петербургской АН. В возрасте двадцати одного года, сформулировал основные законы для расчета токов и напряжений в электрических цепях

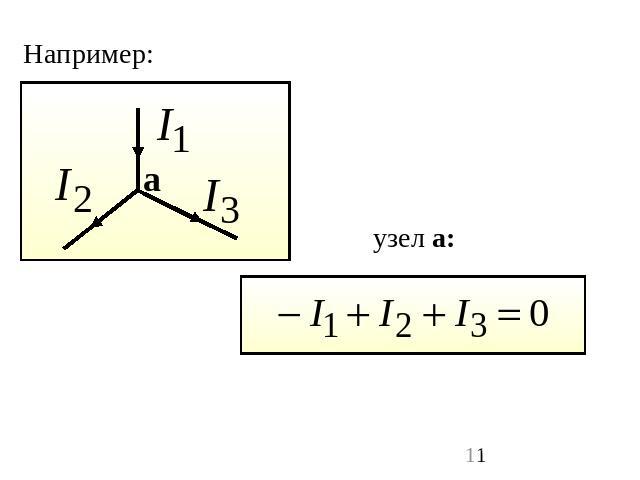
Первый закон Кирхгофа: алгебраическая сумма токов в узле равняется нулю (токи, вытекающие из узла, считаются положительными, а втекающие – отрицательными): Физический смысл этого закона прост: если бы он не выполнялся, в узле непрерывно накапливался бы электрический заряд, а этого никогда не происходит.

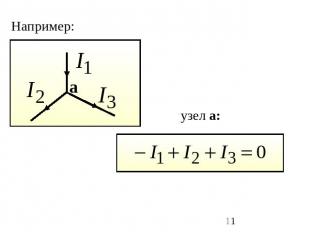
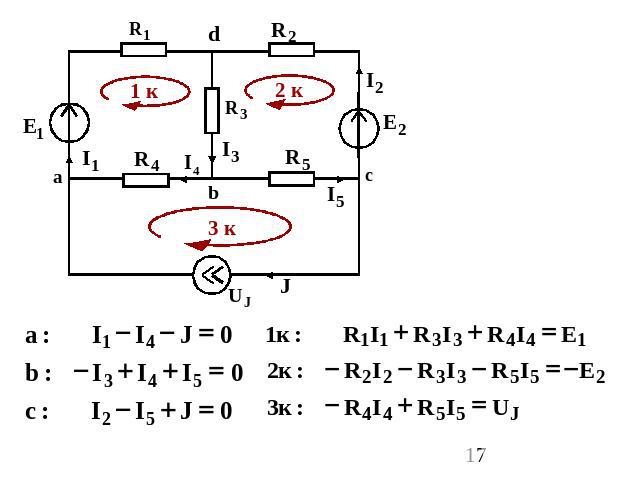
Например: узел а:

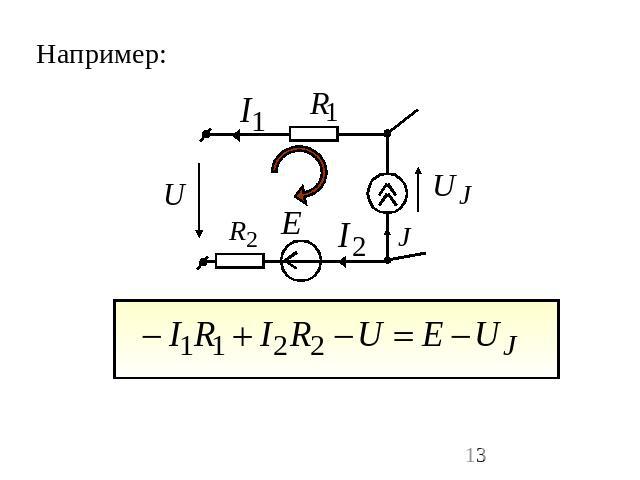
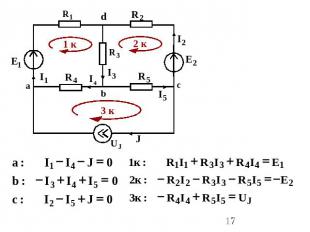
Второй закон Кирхгофа: в контуре алгебраическая сумма падений напряжения на пассивных элементах равна алгебраической сумме ЭДС и напряжений на зажимах источников тока. с “+” берутся все слагаемые, положительное направление которых совпадает с выбранным обходом контура:

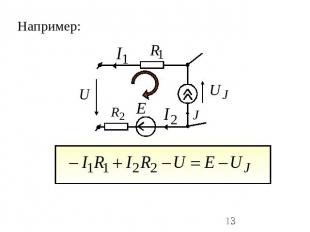
Например:

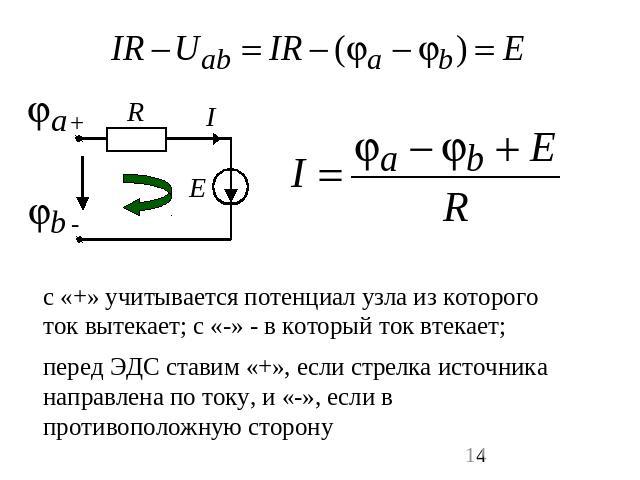
с «+» учитывается потенциал узла из которого ток вытекает; с «-» - в который ток втекает;перед ЭДС ставим «+», если стрелка источника направлена по току, и «-», если в противоположную сторону

1. Метод законов Кирхгофа Решение системы уравнений, составленных по законам Кирхгофа, позволяет определить все токи и напряжения в рассматриваемойцепи

В матричной форме матрица коэффициентов перед неизвестными величинами; матрица источников

В матричной форме Решение системы:

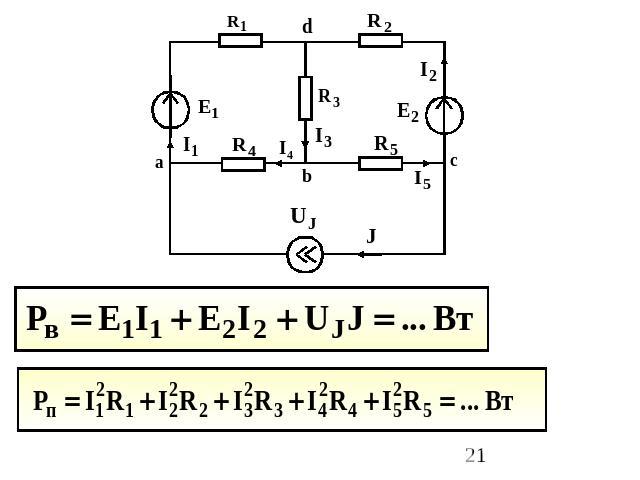
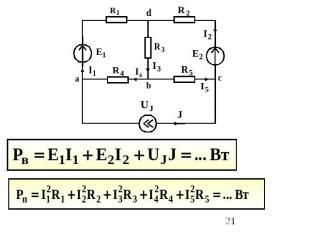
Теорема Телледжена: Для любого момента времени сумма вырабатываемых мощностей источников равна сумме потребляемых мощностей во всех пассивных элементахрассматриваемой цепи

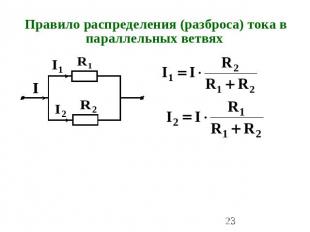
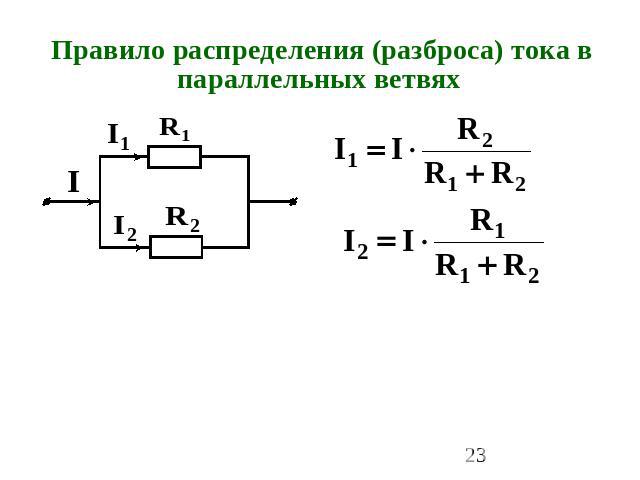
Правило распределения (разброса) тока в параллельных ветвях

2. Метод контурных токов Основан на решении уравнений, составленных по второму закону Кирхгофа и позволяет уменьшить порядок системы уравнений Контурный ток – это ток, текущий в независимом контуре.Число уравнений равно числу независимых контуров: M-N+1

Общая форма записи суммарное сопротивление к-контураконтурный ток к-контураобщее сопротивление между к-контуром и m -контуромсоседний контурный ток m-контурасуммарная ЭДС к-контура

Алгоритм составления уравнений Контурный ток рассматриваемого контура умножается на сумму сопротивлений этого контура.2. К этому произведению дописываются произведения всех соседних контурных токов на общие сопротивления (c “+” если контурные токи обтекают общее сопротивление в одном направлении).3. В правой части уравнения записывается алгебраическая сумма ЭДС контура (с “+”, если направление ЭДС совпадает с направлением контурного тока.

Важно!!!Для контура с источником токауравнение не составляется, так как контурный ток будет равен току источника тока, через источник тока должен проходить только один контурный ток.

Порядок расчета Обозначаются токи ветвейВыбираются контурные токиСоставляется система уравнений по алгоритмуНаходятся контурные токиЧерез контурные токи находятся реальные токи схемы

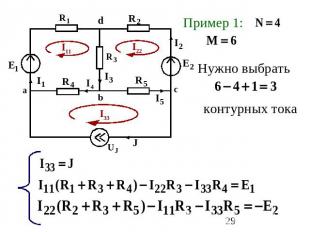
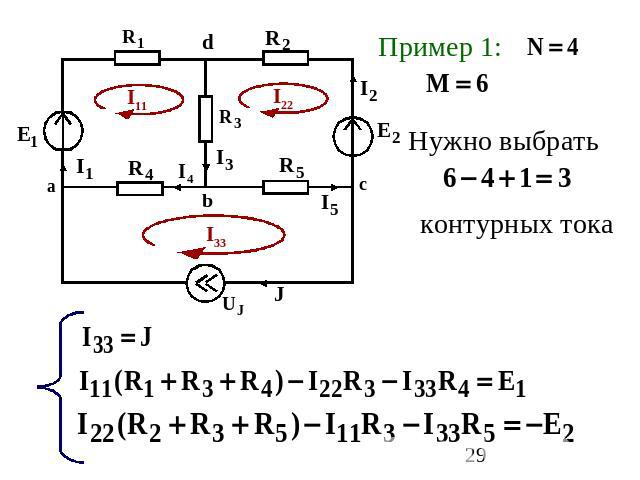
Пример 1: Нужно выбратьконтурных тока

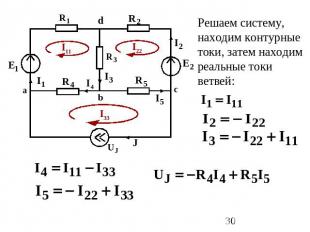
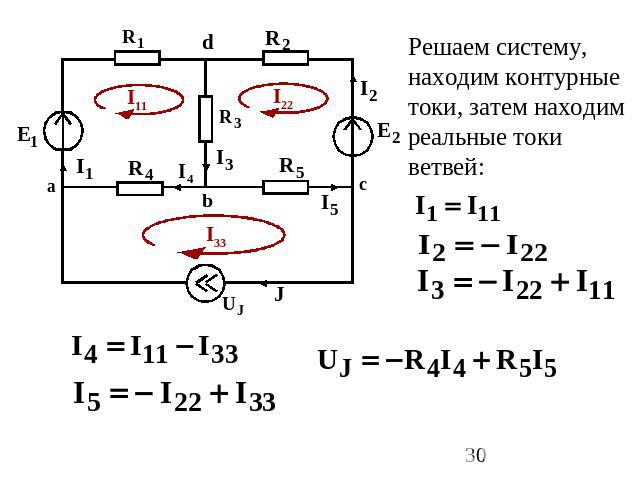
Решаем систему, находим контурные токи, затем находим реальные токи ветвей:

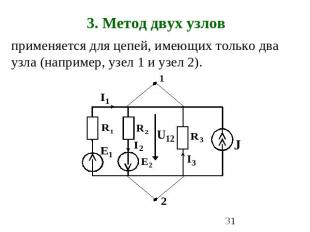
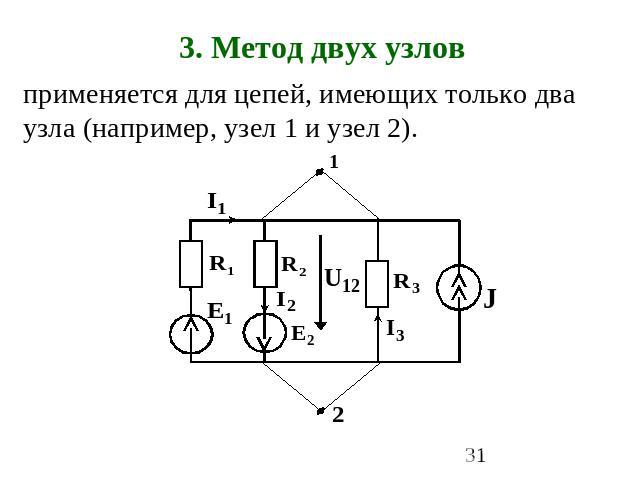
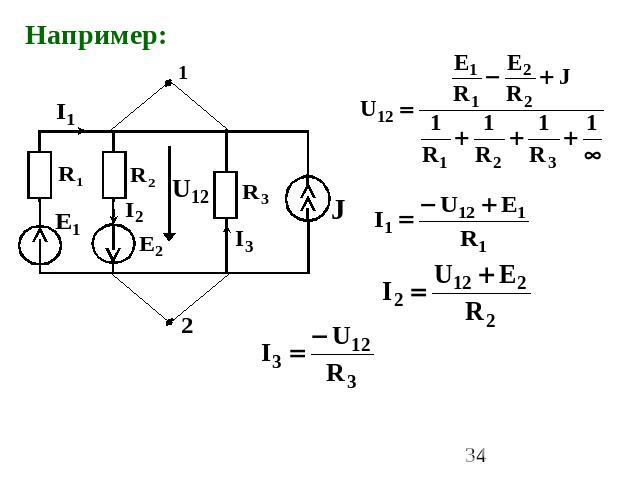
3. Метод двух узлов применяется для цепей, имеющих только два узла (например, узел 1 и узел 2).

Порядок расчета 1. Вычисляется межузловое напряжение, направленное от узла 1 к узлу 2: – алгебраическая сумма отношений ЭДС ветвей к сопротивлениям этих ветвей (с «+», если стрелка ЭДС не совпадает с U12); – алгебраическая сумма токов источников тока (с «+», если его направление не совпадает с U12 );

– сумма проводимостей всех ветвей, соединяющих узлы 1 и 2. 2. Вычисляются токи ветвей по закону Ома: «+», если направление тока Ik в k-ой ветви совпадает с направлением U12 и Ek; Rk – сопротивление k-ой ветви.

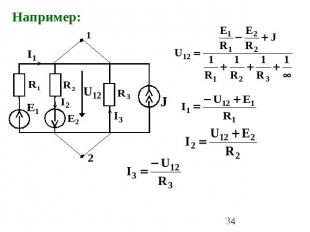
Например: