Презентация на тему: Лекции по физике. Механика

Лекции по физике. Механика Механические колебания. Маятники. Волновые процессы.

Механические колебания Колебаниями называются процессы, происходящие с некоторой долей повторяемостиКлассификация колебанийСвободные (собственные)ВынужденныеПараметрическиеАвтоколебания

Механические колебания Гармонические колебания описываются гармоническими функциями (sin, cos)Процессы в природе часто близки к гармоническимЛюбые колебания можно рассматривать как суперпозицию гармонических

Малые колебания Рассмотрим механическую систему с одной степенью свободы, имеющую минимум потенциальной энергии U(x) в точке x=0Разложим U(x) в ряд Маклорена: U(x)=U(0)+U(0)x+1/2U(0)x2+…из условия минимума U(0)=0 и U(0)>0положим U(0)=0 U(x)=1/2k x2

Малые колебания F=-gradU=-kx – восстанавливающая силаЕсли эта сила действует на тело массой m, то уравнение движения принимает вид:mx=-kx или x+k/mx=0Решение этого уравнения:x=Acos(0t+0), 02=k/m,где A – амплитуда, 0 – начальная фаза,0 – круговая частота, 0t+0 – фаза

Малые колебания Сила трения: Fтр=-rx, где r – коэффициент сопротивленияУравнение движения с учётом силы трения:mx=-kx-rx или x+2x+ 02x=0,где 2=r/m>0. Это уравнение описывает затухающие собственные колебания

Малые колебания Решение уравнения:x=Ae-tcos(t+0), При действии на систему внешней силы f(t) уравнение движения принимает вид: x+2x+ 02x=f(t)(1)Это уравнение описывает вынужденные колебания. Решение будет гармоническим, если f(t) – гармоническая функция: f(t)=F0cos(t)В общем случае 0

Малые колебания Уравнение (1) является линейным дифференциальным уравнением второго порядка с постоянными коэффициентамиЕсли f(t)0, то (1) неоднородное уравнение, если f(t)=0, то однородноеОбщее решение неоднородного уравнения равно сумме общего решения однородного уравнения и какого-либо частного решения неоднородного уравнения

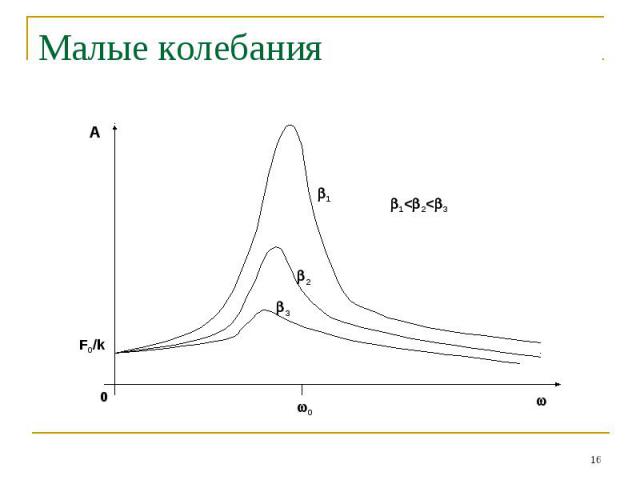
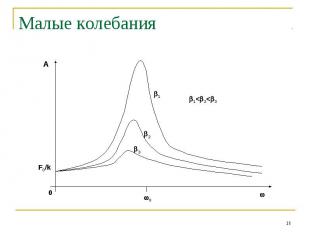
Малые колебания При f(t)=F0cos(t) решение уравнения (1) имеет вид:

Малые колебания Особенности решения:Частота колебаний равна частоте вынуждающей силыПри 0 наступает явление резонанса при котором амплитуда вынужденных колебаний достигает максимумаВынужденные колебания отстают по фазе от вынуждающей силыУгол отставания =/2 при резонансной частоте, 0 при 0 и при

Явление резонанса

Малые колебания

Гармонические колебания x=Acos(0t+0)Период: T=2/0, cЧастота: =1/T=0/2, ГцСкорость: v=x=-A0 sin(0t+0)== A0 cos(0t+0+/2)Ускорение: a=x=-A02 cos(0t+0)== A02 cos(0t+0+)=

Гармонические колебания Значения A и 0 могут быть определены из начальных условий, т.к. при t=0:x0=Acos(0),v0=-A0sin(0)Отсюда получаем:

Гармонические колебания В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно. Кинетическая энергия достигает максимума при прохождении точки равновесия, а потенциальная – в точках максимального отклонения

Сложение колебаний Согласно теореме Фурье негармоническое колебание можно представить как бесконечную сумму гармонических колебаний с частотами кратными частоте исходного колебания:

Пружинный маятник Возвращающая сила: Fн=klУравнение движения: l+(k/m)l=0Частота и период колебаний:

Математический маятник Положение системы задаётся углом отклонения.Уравнение движения:ml2=-mgl или +(g/l)=0Частота и период колебаний:

Гармонические колебания Широкое применение на практике получили генераторы колебаний – устройства в которых возбуждаются и поддерживаются автоколебания. В этих устройствах потери энергии колебательной системы компенсируются за счёт подвода энергии извне с помощью специального механизма

Звуковые колебания Особую роль в жизни людей играют звуковые колебания которые представляют собой колебания частиц окружающей среды (воздух, вода и т.д.). Эти колебания используются для получения информации об окружающем миреСуществуют различные способы возбуждения звуковых колебаний

Конец лекции